A disk sliding with velocity u on a smooth horizontal plane strikes another identical disk kept at rest as shown in the figure. If the impact between the disks is perfectly elastic impact, find velocities of the disks after the impact.
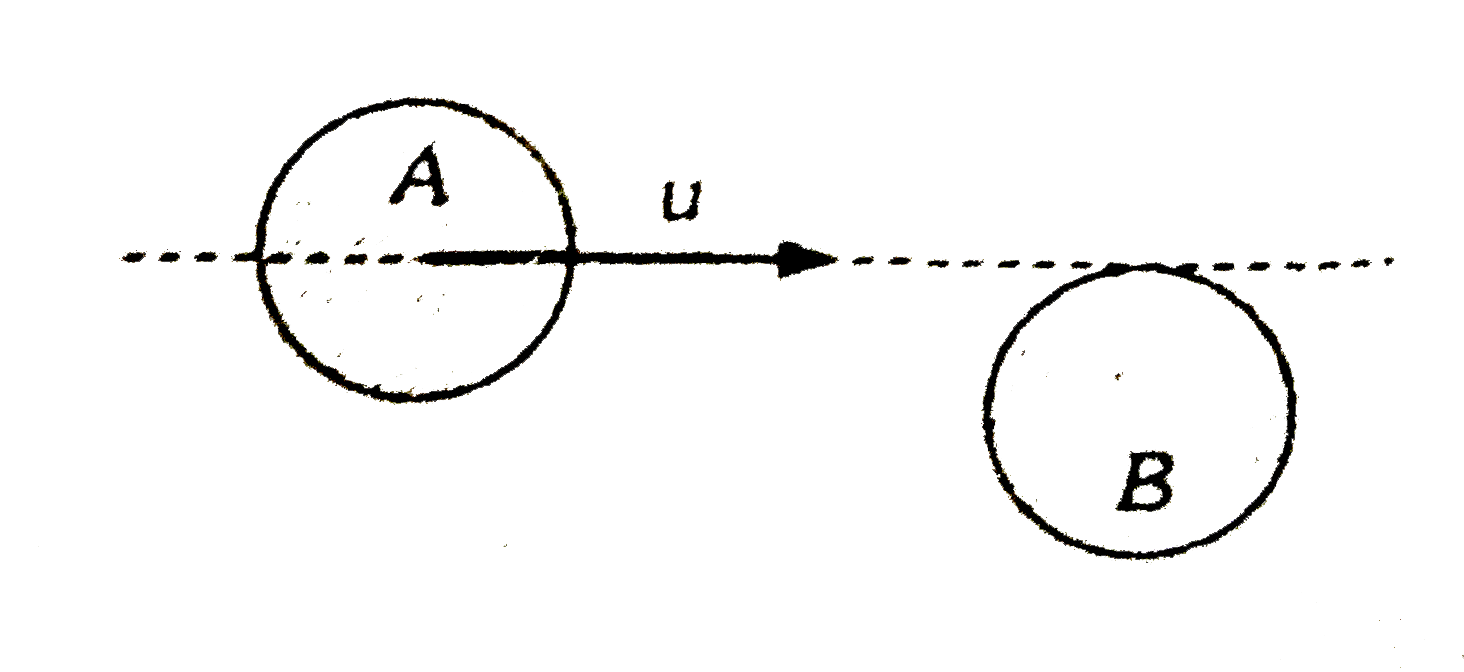 Solution in Gujrati
Solution in Gujrati
We first show velocity components along the t and the n-axis immediately before and after the impact. Angle that the line of impact makes with velocity u is 30∘

Component along t-axis Components of momentum along the t-axis of each disk, considered separately, is conserved. Hence, t-component of velocities of each of the bodies remains unchanged.
vAt=uAt=u2 and vBt=uBt=0 ...(i)
The component along the n-axis of the total momentum of the two bodies is conserved
mBvBn+mAvAn=mBuBn+mAuAn→mvBn+mvAn=m×0+mu√32
vBn+vAn=u√32 ...(ii)
Concept of coefficient of restitution e is applicable only for the n-component velocities.
vBn−VAn=e(uAn−UBn)→ vBn−VAn=u√32 ...(iii)
From equations (ii) and (iii), we have vAn=0 and vBn=u√32 ...(iv)
From equations (i) and(iv) we can write velocities of both the disks.
Topper's Solved these Questions
- CENTRE OF MASSBOOK - ALLEN CHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-I
40 Videos
- CENTRE OF MASSBOOK - ALLEN CHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-II
43 Videos
- BASIC MATHEMATICS USED IN PHYSICS &VECTORS BOOK - ALLEN CHAPTER - BASIC MATHEMATICS USED IN PHYSICS &VECTORS EXERCISE - EXERCISE-IV ASSERTION & REASON
11 Videos
- ELASTICITY, SURFACE TENSION AND FLUID MECHANICSBOOK - ALLEN CHAPTER - ELASTICITY, SURFACE TENSION AND FLUID MECHANICSEXERCISE - Exercise 5 B (Integer Type Questions)
3 Videos
Similar Questions
The centre of mass of a non uniform rod of length L whoose mass per unit length varies as p=kx2/L, (where k is a constant and x is the distance measured form one end) is at the following distances from the same end
View SolutionTwo particle A and B start moving due to their mutual interaction only. If at any tiem 't', →aA and →aB are their respective accelerations, →vA and →vB are their respective velocities, and upto that time WA and WB are the work done on A and B respectively by the mutual force, mA and mB are their masses respectively, then which of the following is alwys correct.
View SolutionAssertion: If the initial and final positions coincide, the displacement is a null vector.
Reason: A physical quantity can not be called a vector, if its magnitude is zero.
View SolutionTwo soap bubbles A and B are kept in a closed chamber where the air is maintained at pressure 8N/m2.The radii of bubbles A and B are 2cm and 4cm, respectively. Surface tension of the soap-water used to make bubbles is 0.04N/m. Find tha ratio nB/nA, where nA and nB are the number of moles of air in bubbles A and B, respectively. [Neglect the effect of gravity.]
View Solution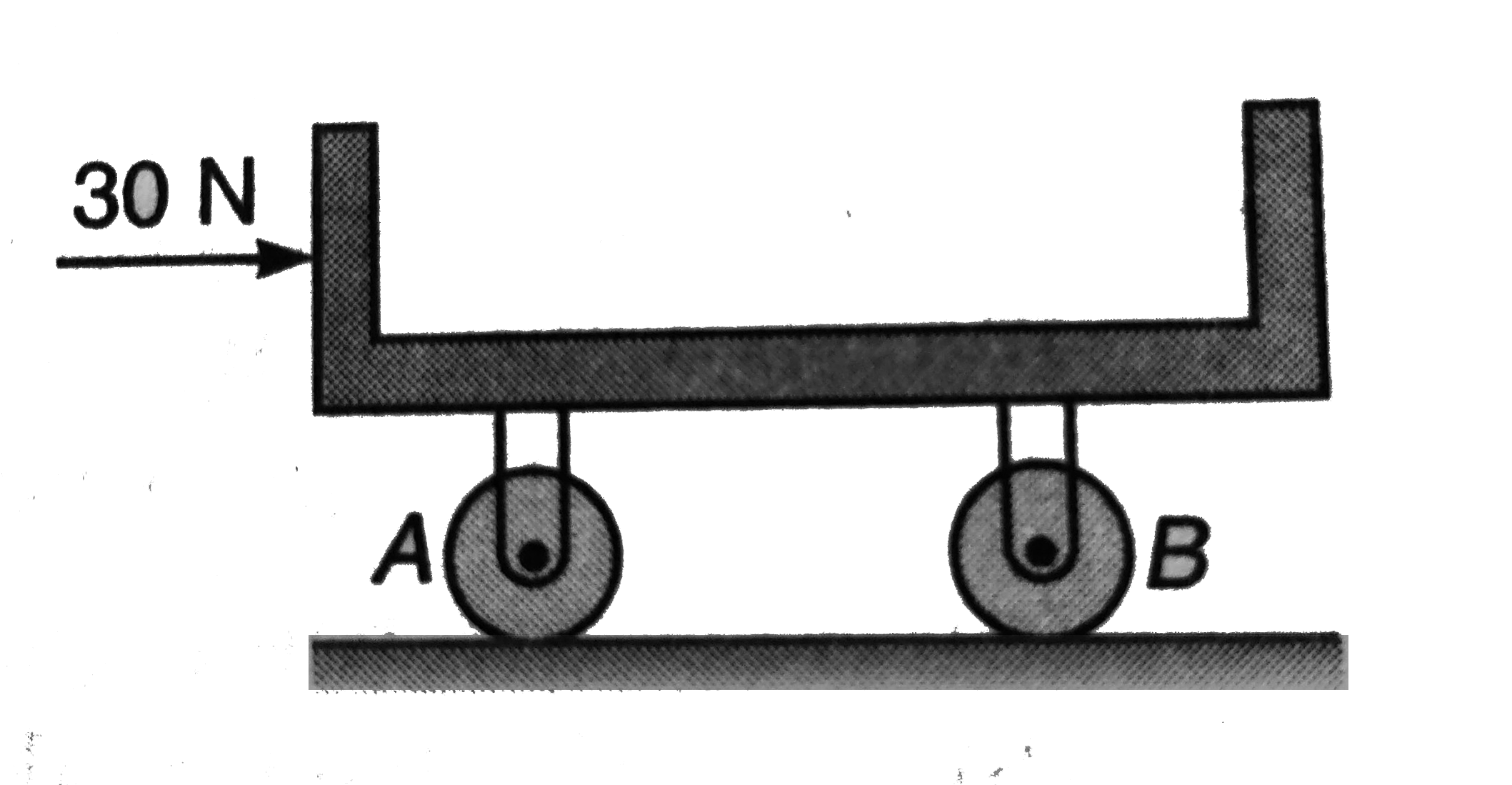
The 9 kg cradle is supported as shown by two uniform disks that roll without sliding at all surfaces of contact. The mass of each disk is m=6kg and the radius of each disk is r=80mm. Knowing that the system is initially at rest, determine the velocity of the cradle after it has moves 250 mm.
View SolutionA positively charged disk is rotated clockwise as shown in Fig. The direction of hte magnetic field at a point A in the plane of the disk is
View SolutionA unifrom solid disk of radius R and mass M is free to rotate on a frictionless pivot through a point on its rim. If the disk is released from rest in the position shown in figure. The speed of the lowest point on the disk in the dashed position is.
 .
.
View SolutionA solid unifrom disk of mass m and radius R is pivoted about a horizontal axis through its centre and a small body of mass m is attached to the rim of the disk. If the disk is released from rest with the small body, initially at the same level as the centre, the angular velocity when the small body reaches the lowest point of the disk is.
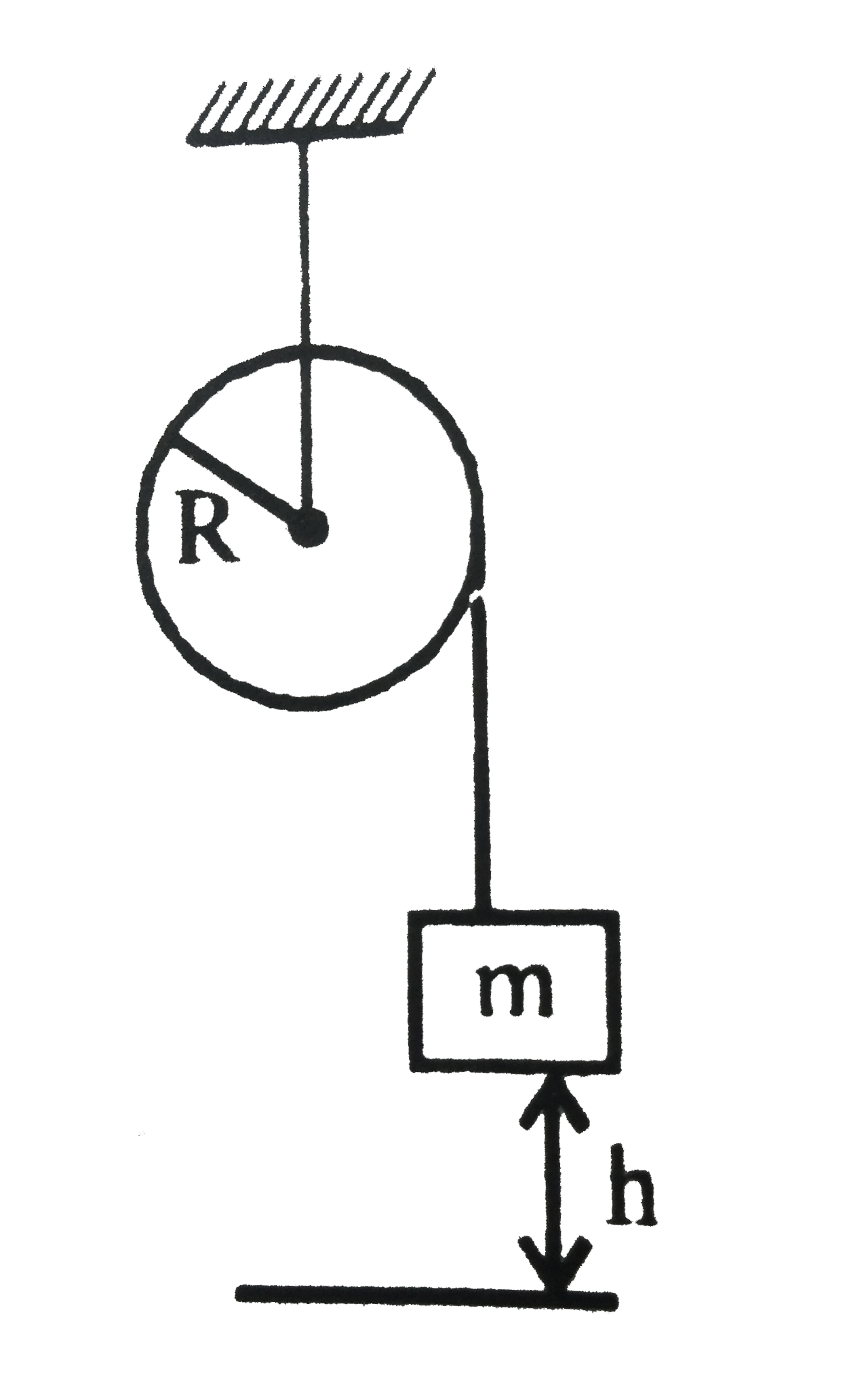
View SolutionA mass m is attached to a pulley through a cord as shown in figure. The pulley is a solid disk with radius R. The cord does not slip on the disk. The mass is released from rest at a height h from the ground and at the instant the mass reaches the ground, the disk is rotating with angular velocity ω. Find the mass of the disk.
 .
.
View SolutionA ball collides with a frictionless wall with velocity u as shown in the figure. Coefficient of restitution for the impact is e. (a) Find expression for the velocity of the ball immediately after the impact. (b) If impact is perfectly elastic what do you observe?
View SolutionA disk A of radious r moving on perfectly smooth surface at a speed v undergoes an elastic collision with an identical stationary disk B. Find the velocity of the disk B after collision if the impact parameter is r/2 as shown in the figure :-
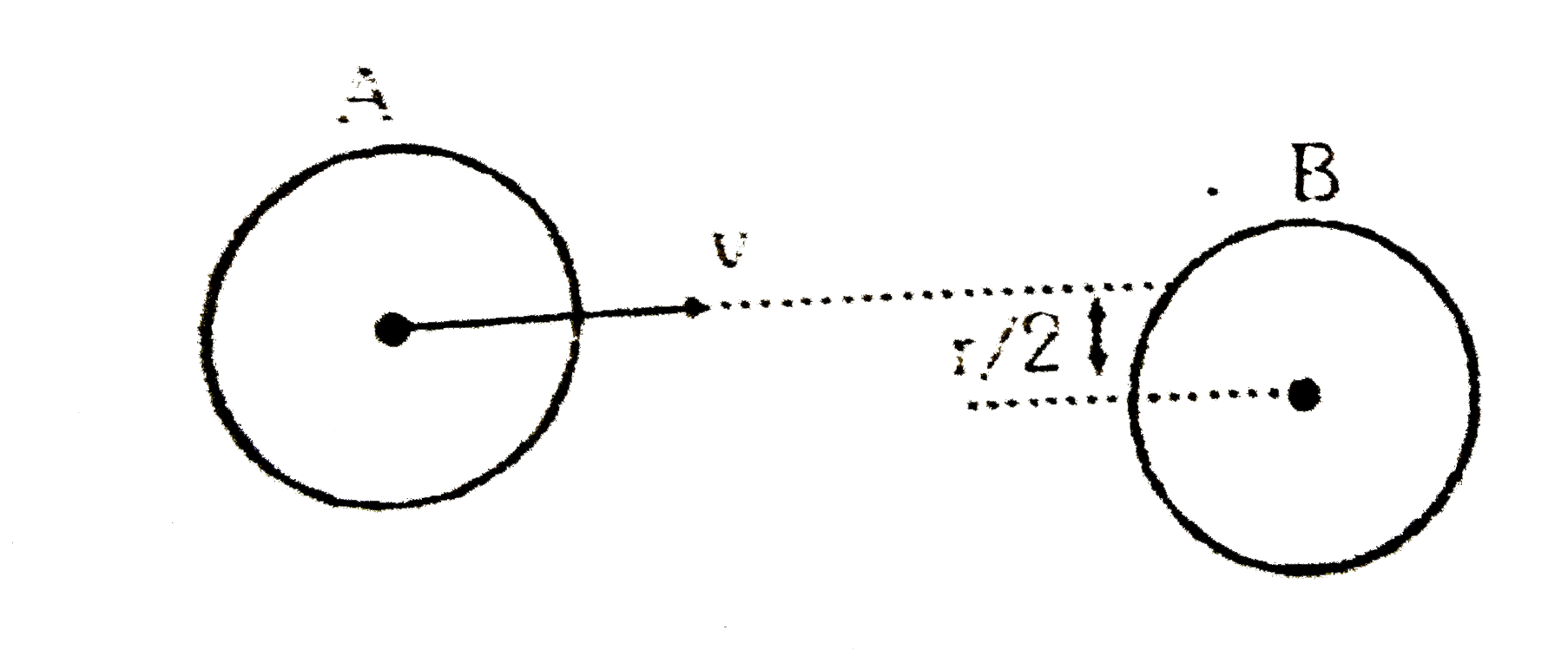
View SolutionA smooth ball A travels towards another identical ball B with a velocity u. Ball B is at rest and the impact parameter d is equal to sqrt(3) R where R is radius of each ball. Due to impact the direction of motion of ball A changes by 30^(@) . Find the velocity of B after the impact. It is given that collision is elastic
View SolutionA 4-kg disk slides over level ice towards the eact at a velocity of 1 meter per second, as shown. The disk strikes a post and rebounds towards the north at the Same speed. The change in the magnitude of the eastward component of the momentum of the disk is:
View SolutionA disk moving on a frictionless horizontal table collides elastically y with another identical disk as shown. The directions of motion of the two disks make angles 0 and phi with the initial line of motion as shown. Then
View SolutionIn an elastic collision between disks A and B of equal mass but unequal radii, A moves along the x-axis and B is stationary before impact. Which of the following is possible after impact?
View Solutionएक गोलीय चकती क्षैतिज सतह पर बिना फिसले लुढ़क रही है तथा चकती का केन्द्र एक समान वेग । से गति कर रहा है चकती के शिरों के किसी बिन्दु पर वेग का मान क्या हो सकता है
View Solution
