A thin sheet of metal of uniform thckness is cut into the shape bounded by the line x=a and y=±kx2, as shown. Find the coordinates of the centre of mass
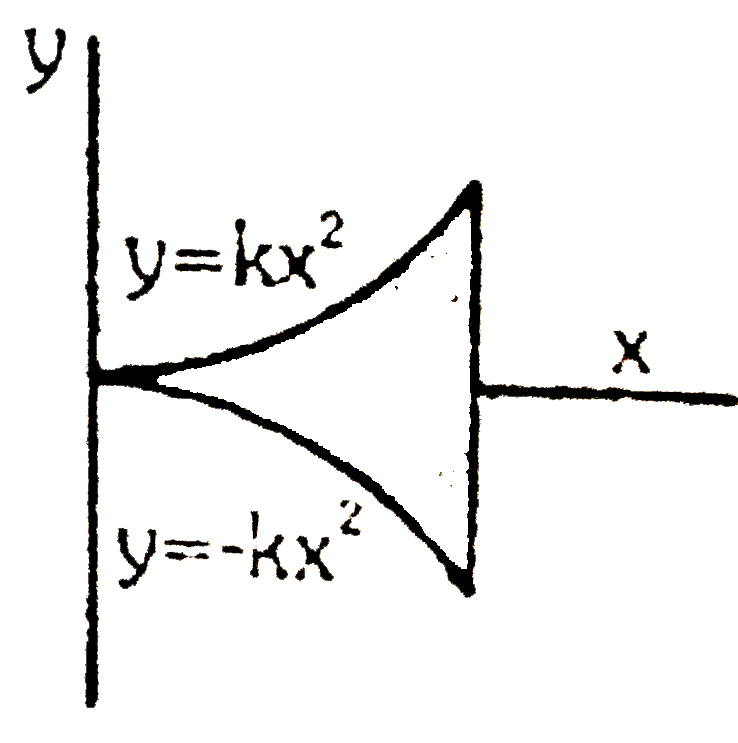 Solution in Gujrati
Solution in Gujrati
The correct Answer is:x=3a4
xcm=∫xdm∫dm=∫a0xρydx∫a0ρydx=34a
Topper's Solved these Questions
- CENTRE OF MASSBOOK - ALLEN CHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-IV B
14 Videos
- CENTRE OF MASSBOOK - ALLEN CHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-V A
20 Videos
- CENTRE OF MASSBOOK - ALLEN CHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-III
41 Videos
- BASIC MATHEMATICS USED IN PHYSICS &VECTORS BOOK - ALLEN CHAPTER - BASIC MATHEMATICS USED IN PHYSICS &VECTORS EXERCISE - EXERCISE-IV ASSERTION & REASON
11 Videos
- ELASTICITY, SURFACE TENSION AND FLUID MECHANICSBOOK - ALLEN CHAPTER - ELASTICITY, SURFACE TENSION AND FLUID MECHANICSEXERCISE - Exercise 5 B (Integer Type Questions)
3 Videos
Similar Questions
A bullet of mass M is fired with a velocity 50m/s at an angle with the horizontal. At the highest point of its trajectory, it collides head-on with a bob of mass 3M suspended by a massless string of length 10/3 metres and gets embeded in the bob. After the collision, the string moves through an angle of 120∘. Find
(i) the angle θ,
(ii) the vertical and horizontal coordinates of the initial position of the bob with respect to the point of firing of the bullet. Take g=10m/s2
View SolutionTwo identical particles move towards each other with velocity 2v and v respectively. The velocity of centre of mass is
View SolutionA particle of mass m, kinetic energy K and momentum p collision head on elastically with another particle of mass 2m at rest. After collision. :
Column IColumn II(A)Momentum of first particle(p)3/4p(B)Momentum of second particle(q)−K/9(C)Kinetic energy of first particle(r)−p/3(D)Kinetic energy of second particle(s)8K9None
View SolutionAssertion: If the initial and final positions coincide, the displacement is a null vector.
Reason: A physical quantity can not be called a vector, if its magnitude is zero.
View SolutionTwo soap bubbles A and B are kept in a closed chamber where the air is maintained at pressure 8N/m2.The radii of bubbles A and B are 2cm and 4cm, respectively. Surface tension of the soap-water used to make bubbles is 0.04N/m. Find tha ratio nB/nA, where nA and nB are the number of moles of air in bubbles A and B, respectively. [Neglect the effect of gravity.]
View SolutionFind the centre of mass of a uniform L shaped lamina (a thin flat plate) with dimension as shown in Fig. The mass of the lamina is 3kg.

View SolutionA uniform piece of metal sheet is cut in the form as shown in the figure. Locate the centre of mass of the piece.
View SolutionA uniform thin rod is bent in the form of closed loop ABCDEFA as shown in the figure. The y- coordinate of the centre of mass of the system is
View SolutionThe coordinates of the centre of mass of a uniform flag -shaped lamina (thin flat plate) of mass 4kg .( The coordinates of the same are shown in the figure) are :
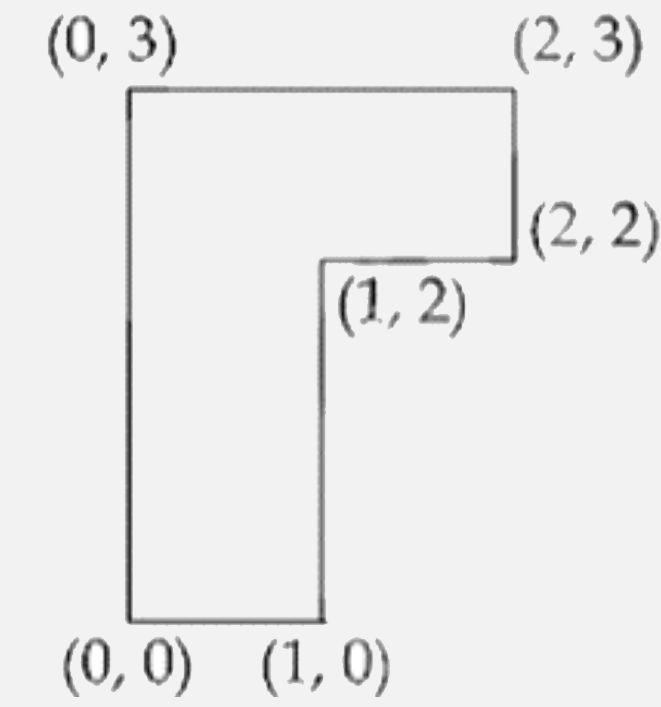
View SolutionFind the centre of mass of a uniform L-shaped lamina (a thin flat plate) with dimensions as shown. The mass of the lamina is 3 kg.
View SolutionFind the centre of mass of a uniform L-shaped lamina (a thin flat plate) with dimensions as shown. The mass of the lamina is 3 kg.
View SolutionFind the centre of mass of a uniform L-shaped lamina (a thin flat plate) with dimensions as shown. The mass of the lamina is 3 kg.
View SolutionFind the centre of mass of a uniform L-shaped lamina (a thin flat plate) with dimensions as shown. The mass of the lamina is 3 kg.
View SolutionFind the centre of mass of a uniform L shaped lamina (a thin flat plate) with dimension as shown in Fig. The mass of the lamina is 3kg.

View SolutionA uniform piece of metal sheet is cut in the form as shown in the fig. Locate the centre of mass of the piece.
View SolutionFind the centre of mass of uniform thin sheet as shown in figure.

View Solution
