A calorie is a unit of heat energy and its value is 4.18J, where 1J=1kg −m2/s2. Suppose we use a new system of units in which unit of mass equals of kg, the unit of length equals β m and the unit of the time is γ sec. Then the value of a calorie in the new system of units:-Solution in Gujrati
4.2α−1β−2γ2
4.2α1β2γ−2
α1β−2γ−2
α−1β2γ−2
The correct Answer is:A
∵1cal=4.2J∴1cal=4.2kgm2s−2
=(4.2α−1β−2γ2)(αkg)(βm)2(γs)−2
Topper's Solved these Questions
- MISCELLANEOUSBOOK - ALLEN CHAPTER - MISCELLANEOUSEXERCISE - Exercise-03
1 Videos
- MISCELLANEOUSBOOK - ALLEN CHAPTER - MISCELLANEOUSEXERCISE - Exercise-04
1 Videos
- MISCELLANEOUSBOOK - ALLEN CHAPTER - MISCELLANEOUSEXERCISE - Exersice -05(B)
20 Videos
- KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)BOOK - ALLEN CHAPTER - KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)EXERCISE - BEGINNER S BOX-7
8 Videos
- PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT BOOK - ALLEN CHAPTER - PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT EXERCISE - EXERCISE-IV
7 Videos
Similar Questions
Two parallel metallic plates have surface charge densities σ1 and σ2 as shown in figure.
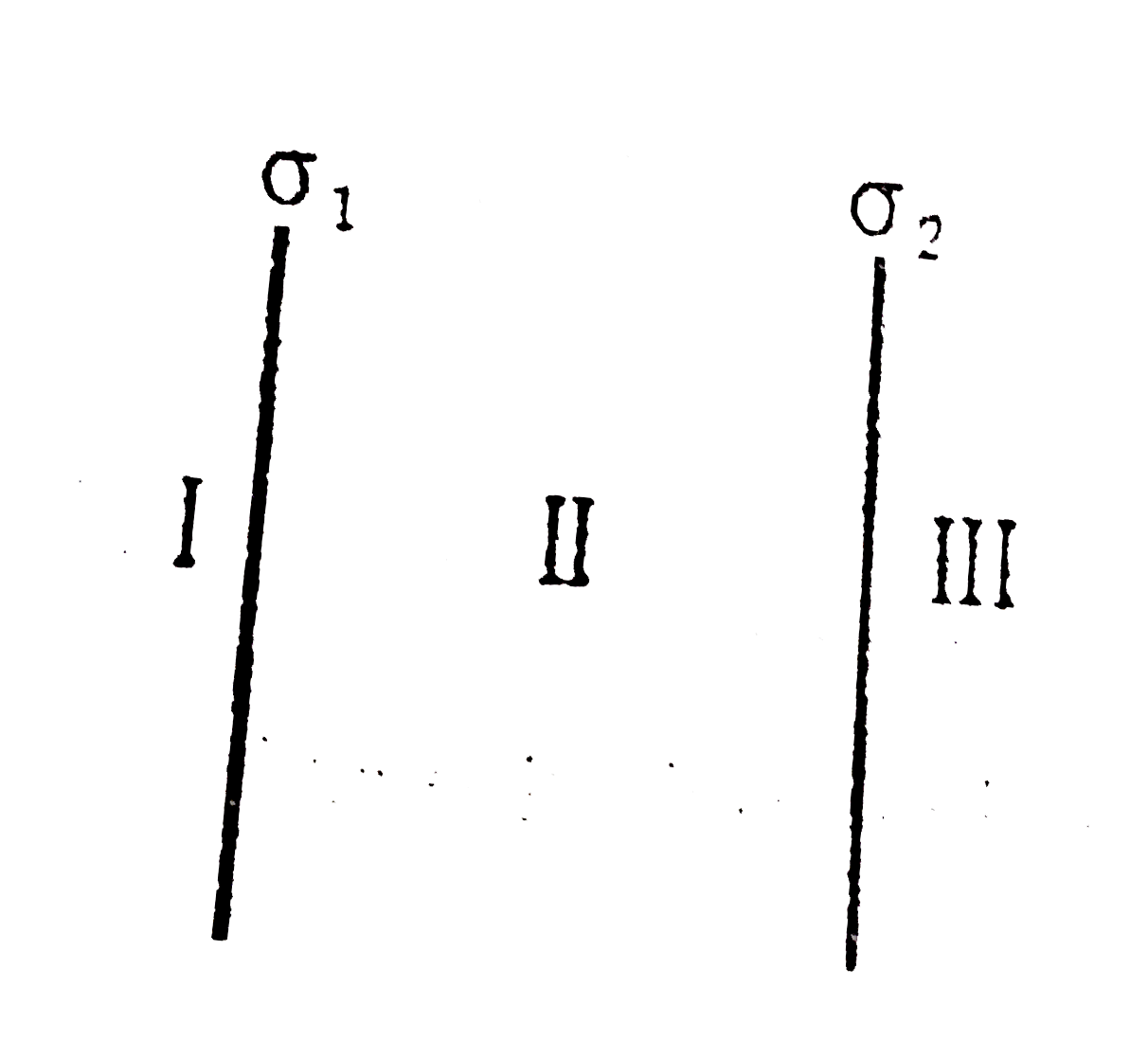
Column-IColumn-II(A)If σ1+σ2=0(p)Electric field in region III is towards right(B)Ifσ1+σ2>0(q)Electric field in region I is zero(C)If σ1+σ2<0(r)Electric field in region I is towards roght(s)Nothing can be said
View SolutionIn each situation of Column-I two elelctric dipoles having moments →p1 and →p1 of same magnitude (that is ,p1=p2) are placed on x-axis symmetrically about origin in different orientations as shown. In column-II certain inferences are drawn for these two dipoles. Then match the different orientations of dipole in column-I with the corresponding result in column-II.

View SolutionPlanck's constant has dimensions …………….
View SolutionA football player kicks a ball at an angle of 30∘ with an initial speed of 20 m/s. Assuming that the ball travels in a vertical plane, calculate (a) the time at which the ball reaches the highest point (b) the maximum height reached (c) the horizontal range of the ball (d) the time for which the ball is in the air, (g=10m/s2)
View SolutionAssertion : Gravitational forces do not depend on the medium between the masses.
Reason : Mediating particle responsible for gravitational force is graviton.
View SolutionA calorie is a unit of heat or energy and it equals about 4.2J,where1J=1kgm2s−2. Suppose we employ a system of units in which the unit of mass equals αkg, the unit of length equals is βm , the unit of time is γs. Show tthat a calorie has a magnitude 4.2α−1β−1γ2 in terms of the new units.
View Solutionऊष्मा (परागमन में ऊर्जा) का मात्रक कैलोरी है और यह लगभग 4.2 J के बराबर है, जहाँ 1J=1kgm2s−2 | मान लीजिये कि हम मात्रकों की कोई ऐसी प्रणाली उपयोग करते हैं जिससे द्रव्यमान का मात्रक αkg के बराबर है, लंबाई का मात्रक के बराबर है, समय का मात्रक γs के बराबर है । यह प्रदर्शित कीजिये कि नए मात्रकों के पदों में कैलोरी का परिणाम 4.2α−1β−2γ2 है ।
View Solutionऊष्मा या ऊर्जा का मात्रक कैलोरी है और यह लगभग 4.2 J के बराबर है, जहाँ 1 J = 1 kg m2s−2 । मान लीजिए कि हम मात्रको कि कोई ऐसी प्रणाली उपयोग करते हैं जिससे द्रव्यमान का मात्रक α kg के बराबर है, लम्बाई का मात्रक βm के बराबर है, समय का मात्रक γ s के बराबर है । यह प्रदर्शित कीजिए कि न्य मात्रको के पदों में कैलोरी का परिमाण 4.2α−1β−2γ2 है ।
View SolutionA calorie is a unit of heat or energy and it equals about 4.2J,where1J=1kgm2s−2. Suppose we employ a system of units in which the unit of mass equals αkg, the unit of length equals is βm , the unit of time is γs. Show tthat a calorie has a magnitude 4.2α−1β−1γ2 in terms of the new units.
View Solution1 calorie=4.2 J where IJ= 1 kg m^2s^-2 . Suppose we employ a system of units in which the unit of mass is alpha kg, the unit of length is beta m and the unit of time gamma s , show that a calorie has a magnitude 4.2alpha^-1beta^-2gamma^-2 in the new system.
View SolutionA calorie is a unit of heat or energy and it equals about 4.2 j where 1 J = 1 kg . m2.S−2 . Suppose we employ a system of units in which the unit of mass equals α kg the unit of length equals βm and the unit of time is λs. Show the a calorie has a magnitude 4.2α−1β−2γ2 in terms of the new units.
View SolutionA calorie is a unit of heat or energy and it equals 4.2 J where 1J = 1 kg m^(2)s^(-2) . Suppose we employ a system of units in which unit of mass is alpha kg. unit of length is beta m, unit of time is gamma . What will be magnitude of calorie in terms of this new system?
View SolutionA calorie is a unit of heat (energy in transit) and it equals about 4.2 J where 1J= 1kgm2s−2. Suppose we employ a system of units in which the unit of mass equals α kg, the unit of length equals βm, the unit of time is γs. Show that a calorie has a magnitude 4.2α−1β−2γ2 in terms of the new units.
View SolutionA calorie is a unit of heat or energy and it equals about 4.2J,where1J=1kgm2s−2. Suppose we employ a system of units in which the unit of mass equals αkg, the unit of length equals is βm , the unit of time is γs. Show tthat a calorie has a magnitude 4.2α−1β−1γ2 in terms of the new units.
View SolutionThe calorie is a unit of heat or energy and it equals about 4.2 J where 1J=1kgm2s−2. Suppose we employ a system of units in which the unit of mass equals α kg, the unit of length equals β m and the unit of time isγ s. Show that the calorie has a magnitude of 4.2α−1β−2γ2 in terms of the new units.
View SolutionA calorie is a unit of heat or energy and it equals about 4.2J,where1J=1kgm2s−2. Suppose we employ a system of units in which the unit of mass equals αkg, the unit of length equals is βm , the unit of time is γs. Show tthat a calorie has a magnitude 4.2α−1β−1γ2 in terms of the new units.
View Solution
