In the relation, P=αβeαZkθP is pressure, Z is distance, k is Boltzmann constant and θ is the temperature. The dimensional formula of β will be-Solution in Gujrati
[M0L2T0]
[ML2T]
[ML0T−1]
[M0L2T−1]
The correct Answer is:A
Dimension formula of Boltzman constant
k→[M1L2T−2θ−1]
α[L1][M1L2T−2θ−1][θ−1]=M0L0T0θ0
α=[M1L1T−2],β=[M1L1T−2][M1L−1T−2]=[L2]
Topper's Solved these Questions
- MISCELLANEOUSBOOK - ALLEN CHAPTER - MISCELLANEOUSEXERCISE - Exercise-02
77 Videos
- MISCELLANEOUSBOOK - ALLEN CHAPTER - MISCELLANEOUSEXERCISE - Exercise-03
1 Videos
- MISCELLANEOUSBOOK - ALLEN CHAPTER - MISCELLANEOUSEXERCISE - EXERCISE-5(A)
15 Videos
- KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)BOOK - ALLEN CHAPTER - KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)EXERCISE - BEGINNER S BOX-7
8 Videos
- PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT BOOK - ALLEN CHAPTER - PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT EXERCISE - EXERCISE-IV
7 Videos
Similar Questions
A ladder 5m long is leaning against a wall. The foot of the ladder is pulled out along the ground away from from the wall at a rate of 2m/s. How fast is the height of ladder on the decreasing at the instant when the foot of the ladder is 4m away from the wall?
View SolutionTwo parallel metallic plates have surface charge densities σ1 and σ2 as shown in figure.
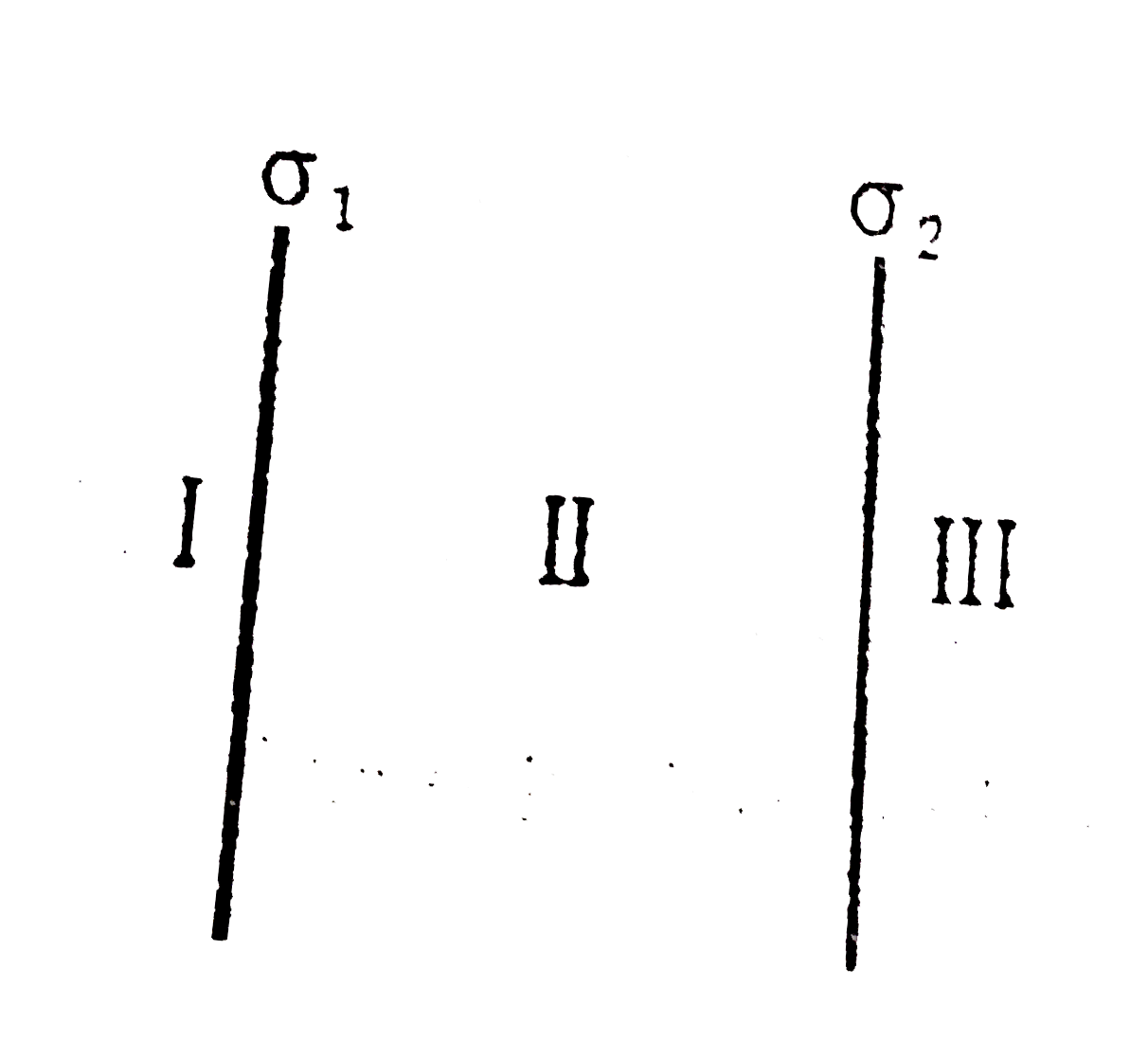
Column-IColumn-II(A)If σ1+σ2=0(p)Electric field in region III is towards right(B)Ifσ1+σ2>0(q)Electric field in region I is zero(C)If σ1+σ2<0(r)Electric field in region I is towards roght(s)Nothing can be said
View SolutionIdentify the pair whose dimensions are equal
View SolutionA football player kicks a ball at an angle of 30∘ with an initial speed of 20 m/s. Assuming that the ball travels in a vertical plane, calculate (a) the time at which the ball reaches the highest point (b) the maximum height reached (c) the horizontal range of the ball (d) the time for which the ball is in the air, (g=10m/s2)
View SolutionAssertion : Gravitational forces do not depend on the medium between the masses.
Reason : Mediating particle responsible for gravitational force is graviton.
View SolutionPressure depends on distance as, P=αβexp(−αzkθ), where α,β are constants, z is distance as , k is Boltzman's constant and θ is tempreature. The dimension of beta are
View SolutionIn the relaction p = (a)/(beta) e ^((aZ)/(k theta ) , p is pressure Z is distance .k is Boltamann constant and theta is the teperations . The dimensional formula of beta will be
View SolutionIn the relation P = (alpha)/(beta) e^(-alphaz//k theta),P is preesure, K is Botzmann's constant, Z is distance and theta is temperature. The dimensional formula of beta wll be
View SolutionIn the relation P = (alpha)/(beta) e^((alpha Z)/(k theta)) , P is pressure, Z is height, k is Boltzmann constant and theta is the temperature. Find the dimensions of alpha and beta
View SolutionIn the relation, P=alpha/beta e^((alphaZ)/(ktheta))P is pressure, Z is distance, k is Boltzmann constant and theta is the temperature. The dimensional formula of beta will be-
View SolutionIn the relation: P=(alpha)/(beta)e^(-(alphaZ)/(ktheta)),P is pressure Z is distance k is Boltzmann constant and theta ils the temperature. The dimensional formula of beta will bes
View SolutionIn the releation p=αβe−azkθ, where p is the pressure z is distance k is Boltzmann constant and θ is the temperature the dimensional formula β will be
View Solutionदूरी z के साथ दाब P का विचरण, P=αβe−az/kθ से व्यक्त किया जाता है, जहाँ α,β नियतांक हैं, k बोल्ट्समान नियतांक तथा θ ताप है । β का विमीय सूत्र होगा :
View SolutionIn the relation P=αβe−αz/kθ
where P=pressurez=distancek=Boltzman's constantθ=Temperature
The dimensional formula of β will be :
View SolutionPressure depends on distance as P=αβexp(−αzkθ) where αβ are constants z is distance k is Boltzmann is constant and θ is temperature. The dimension of β are
View SolutionIn the relation P=αβe−αzkθ is pressure, z is distance, k is Boltzmann constant and θ is the temperature. The dimensional formula of β will be
View Solution
