Some physical quanties are given in Column I and some possible SI units in which these quantities may be expressed are given in Column II. Match the physical quantities in Column I with the units in Column II.
Column IColumn II(A)GMeMs(p)(volt)(coulomb)(metre)G−universal gravitational constantMe−mass of the earth,Ms−mass of the sun(B)3RTM(q)(kilogram)(metre)3(second)−2R−universal gas constant,T−absolute temperature, M- molar mass(C)F2q2B2(r)(metre)2(second)−2F−force,q−charge,B−magnetic field(D)GMeRe(s)(farad)(volt)2(kg)−1G−universal gravitational constant,Me−mass of the earth,Re−radius of the earth.Solution in Gujrati
The correct Answer is:(A) PQ, (B) RS, (C) RS, (D) RS
Match the column
(A) F=GMeMsR2
GMeMs=F×L2=Work×Metre
=Coulomb×Volt×Metre
=ML2T−2×Metre=(kg)(Metre)3(S)−2
(B) 32RT= kinetic energy
3RTM=v2⇒(Metre)2(S)−2
12QV= Energy
⇒QVM=Energym=(farad)(volt)2kg
(C) F2q2B2=q2∈2q2B2⇒(∈B)2=v2⇒(r,s)
(D) GMeR=Work domeMass⇒(Velocity)2⇒(r,s)
Topper's Solved these Questions
- MISCELLANEOUSBOOK - ALLEN CHAPTER - MISCELLANEOUSEXERCISE - Exercise-02
77 Videos
- MISCELLANEOUSBOOK - ALLEN CHAPTER - MISCELLANEOUSEXERCISE - Exercise-03
1 Videos
- MISCELLANEOUSBOOK - ALLEN CHAPTER - MISCELLANEOUSEXERCISE - EXERCISE-5(A)
15 Videos
- KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)BOOK - ALLEN CHAPTER - KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)EXERCISE - BEGINNER S BOX-7
8 Videos
- PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT BOOK - ALLEN CHAPTER - PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT EXERCISE - EXERCISE-IV
7 Videos
Similar Questions
A ladder 5m long is leaning against a wall. The foot of the ladder is pulled out along the ground away from from the wall at a rate of 2m/s. How fast is the height of ladder on the decreasing at the instant when the foot of the ladder is 4m away from the wall?
View SolutionTwo parallel metallic plates have surface charge densities σ1 and σ2 as shown in figure.
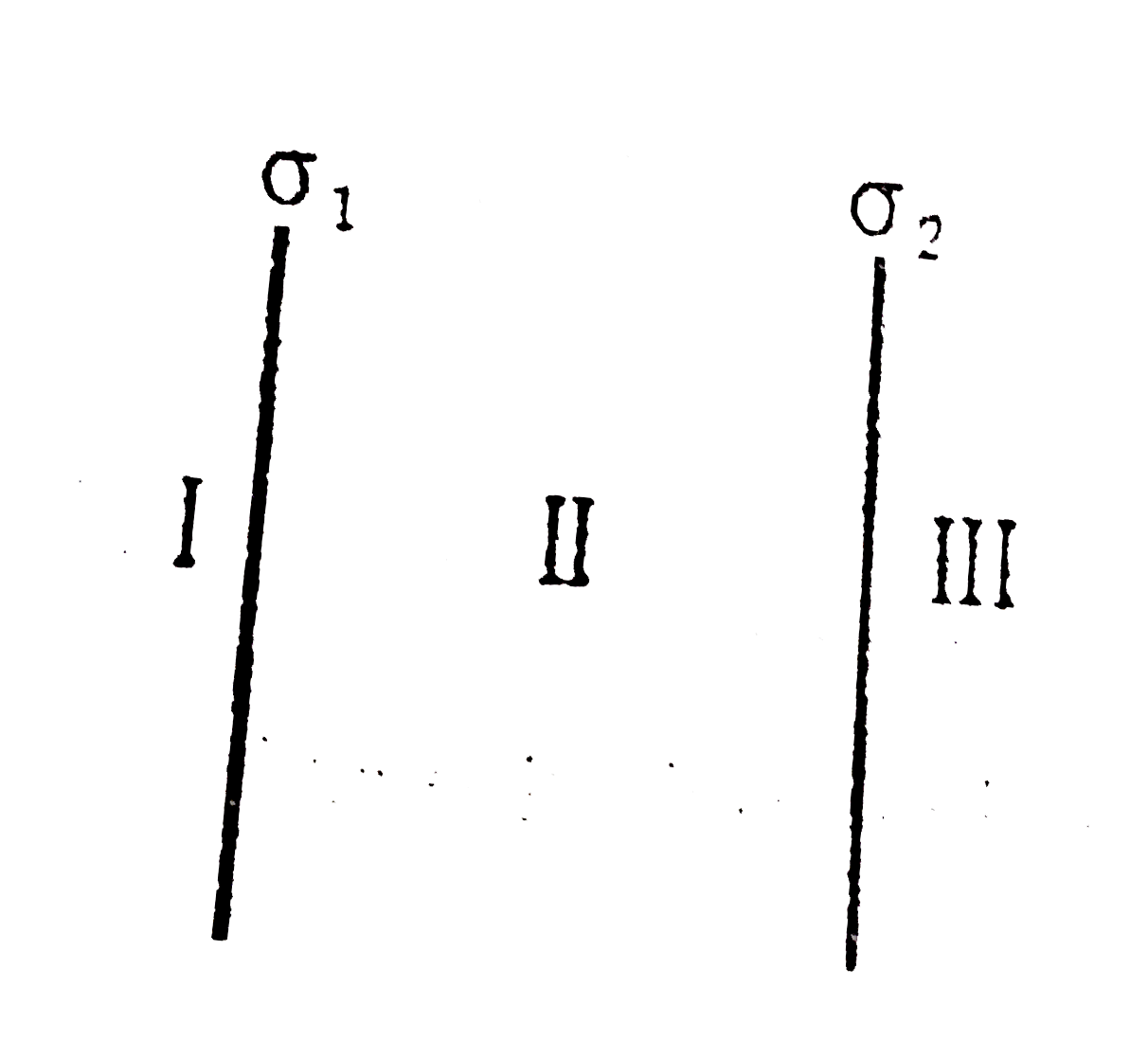
Column-IColumn-II(A)If σ1+σ2=0(p)Electric field in region III is towards right(B)Ifσ1+σ2>0(q)Electric field in region I is zero(C)If σ1+σ2<0(r)Electric field in region I is towards roght(s)Nothing can be said
View SolutionIdentify the pair whose dimensions are equal
View SolutionA football player kicks a ball at an angle of 30∘ with an initial speed of 20 m/s. Assuming that the ball travels in a vertical plane, calculate (a) the time at which the ball reaches the highest point (b) the maximum height reached (c) the horizontal range of the ball (d) the time for which the ball is in the air, (g=10m/s2)
View SolutionAssertion : Gravitational forces do not depend on the medium between the masses.
Reason : Mediating particle responsible for gravitational force is graviton.
View SolutionShow that angular momentum of a satellite of mass M_(s) revolving around earth of mass M_(e) in an orbit of radius r is sqrt(GM_(s)^(2)M_(e)r) .
View SolutionColumn IColumn II(A)Moment of inertia(p)newton/metre2(B)Surface tension(q)kg/(metre-sec)(C)Angular acceleration(r)kg-metre2(D)Coefficient of viscosity(s)newton/metre(E)Modulus of elasticity(t)radian/sec2
View SolutionSome physical quanties are given in Column I and some possible SI units in which these quantities may be expressed are given in Column II. Match the physical quantities in Column I with the units in Column II.
Column IColumn II(A)GMeMs(p)(volt)(coulomb)(metre)G−universal gravitational constantMe−mass of the earth,Ms−mass of the sun(B)3RTM(q)(kilogram)(metre)3(second)−2R−universal gas constant,T−absolute temperature, M- molar mass(C)F2q2B2(r)(metre)2(second)−2F−force,q−charge,B−magnetic field(D)GMeRe(s)(farad)(volt)2(kg)−1G−universal gravitational constant,Me−mass of the earth,Re−radius of the earth.
View SolutionQ is energy released in the decay m_(x) is atomic mass of parent nucleus m_(y) is atomic mass of daughter nucleus and m_(e) is mass of elctron then match the following:
Column-IColumn-II(A)k capture(P)Q=(mx−my)c2(B)β−decay(Q)Q=(mx−my−mc)c2(C)β+decay(R)Q=(mx−my−2me)c2(S)Q=(mx−my+2me)c2
View SolutionThe escape velocity of a sphere of mass m is given by (G= univesal gravitational constant, Me= mass of the earth and Re= radius of the earth)
View SolutionSome physical quantities are given in Column I and some possible SI units in which these quantities may be expressed are given in Column II. Match the physical quantities in Column I with the units in column II and indicate your answer by darkening appropriate bubbles in the 4×4 matrix given in the ORS.
Coloumn-IColumn-II(A)GMeMs(P)(volt)(coulomb)(meter)G-universal gravitational ContantMe−mass of the earthMs−mass of the Sun(B)3RT3(Q)(kilogram)(metre)3R−universal gas constantT−absolute temperatureM−molar mass(C)F2q2B2(R)(metre)2(second)−2F−forceq−chargeB−magnetic field(D)GMeRe(S)(farad)(volt)2(kg)−1G−universal gravitational constantMe−mass of the earthRe−radius of the earth
View SolutionMatch the units given in column-I with the physical quantities in column -II : [Here N-newton, kg -kilogram, s-second , m-metre]
View Solution{:(, "column"-I,, "column-II"),((a) ,"change on electrons (magnitude)", (p) ,1.6022xx10^(-19)C),((b),ed//m_(e),(q),1.758820xx10^(11)CKg^(1)),((c ) , "mass of prton ".m_(p),(r),1.00867u),((d),"Mass of nueutron"m_(n),(s),1.00727u),(,,(t),4.8xx10^(-10)"esu"):}
View SolutionMatch the Column I with Column II
For a satellite in circular orbit
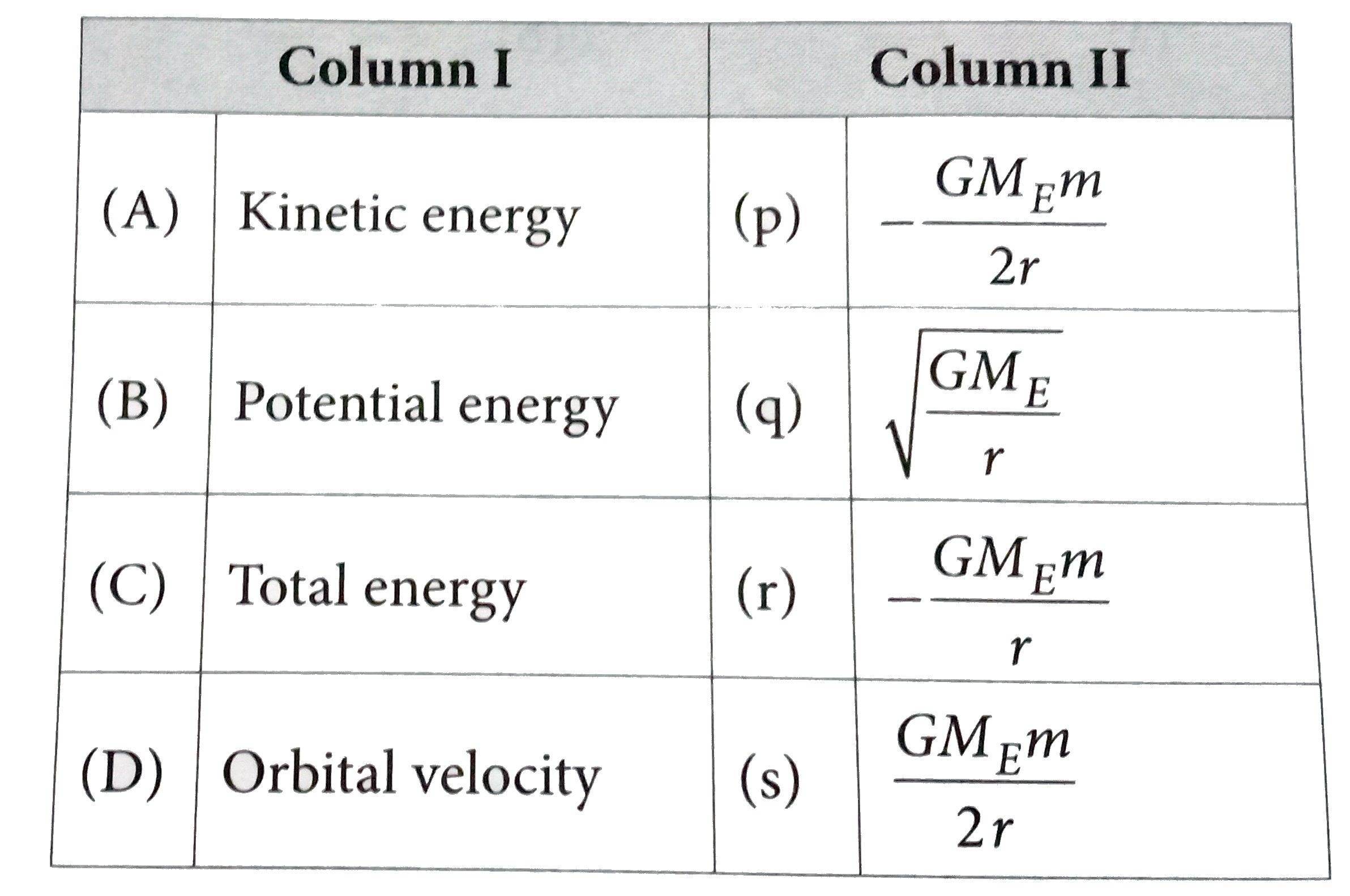
(where ME is the mass of the earth , m is the mass of the satellite and r is the radius of the orbit )
View SolutionColumn IColumn II(A)GMeMs(p)[M2L2T−3](B)3RTM(q)[ML3T−2](C)F2q2B2(r)[L2T−2](D)GMeRe(s)None
View Solutionयदि पृथ्वी का द्रव्यमान Me तथा त्रिज्या Re है, तो गुरुत्वीय त्वरण g तथा गुरुत्वाकर्षण स्थिरांक G में अनुपात है :
View Solution
