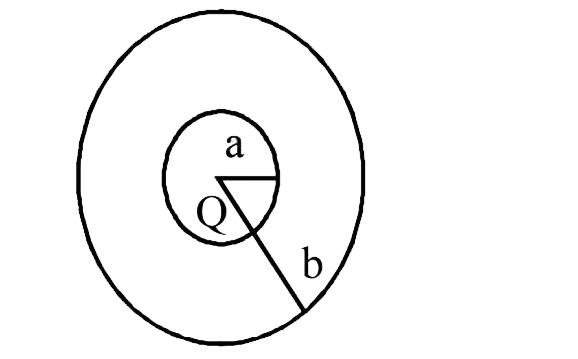
The region between two concentric spheres of radii 'a' and 'b', respectively (see figure), have volume charge density ρ=Ar, where A is a constant and r is the distance from the centre. At the centre of the spheres is a point charge Q. The value of A such that the electric field in the region between the spheres will be constant, is:
 Solution in Gujrati
Solution in Gujrati
2Qπa2
Q2πa2
Q2π(b2−a2)
2Qπ(a2−b2)
The correct Answer is:B
Gaussian surface at distance r from center
Q+r∫aAr4πr2dr∈0=E4πr2
E=Q+2πAr2−2πAa24πr2∈0
make E independent of r then
Q−2πa2A=0⇒A=Q2πa2

Topper's Solved these Questions
- BOOK - ALLEN CHAPTER - MISCELLANEOUSEXERCISE - Exercise-05(B)19videos
MISCELLANEOUS
- BOOK - ALLEN CHAPTER - MISCELLANEOUSEXERCISE - MCQ s WITH ONE OR MORE THAN ONE CORRECT ANSWER6videos
MISCELLANEOUS
- BOOK - ALLEN CHAPTER - MISCELLANEOUSEXERCISE - Exersice-04[B]16videos
MISCELLANEOUS
- BOOK - ALLEN CHAPTER - KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)EXERCISE - BEGINNER S BOX-78videos
KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)
- BOOK - ALLEN CHAPTER - PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT EXERCISE - EXERCISE-IV7videos
PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT
Similar Questions
A charge +q is fixed at each of the points x=x0, x=3x0, x=5x0,…………x=∞ on the x axis, and a charge −q is fixed at each of the points x=2x0, x=4x0, x=6x0, …………x=∞. Here x0 is a positive constant. Take the electric potential at a point due to a charge Q at a distance r from it to be Q/(4πε0r).Then, the potential at the origin due to the above system of
09:15View SolutionA positively charged thin metal ring of radius R is fixed in the xy plane with its centre at the origin O. A negatively charged particle P is released from rest at the point (0,0,z0) where z0>0. Then the motion of P is
05:25View SolutionTwo small balls having the same mass and charge and located on the same vertical at heights h1 and h2 are thrown in the same direction along the horizontal at the same velocity v. The first ball touches the ground at a horizontal distance R from the initial vertical position. At what height h2 will the second ball be at this instant? Neglect any frictional resistance of air and the effect of any induced charge on the ground.
View SolutionA football player kicks a ball at an angle of 30∘ with an initial speed of 20 m/s. Assuming that the ball travels in a vertical plane, calculate (a) the time at which the ball reaches the highest point (b) the maximum height reached (c) the horizontal range of the ball (d) the time for which the ball is in the air, (g=10m/s2)
05:38View SolutionAssertion : Gravitational forces do not depend on the medium between the masses.
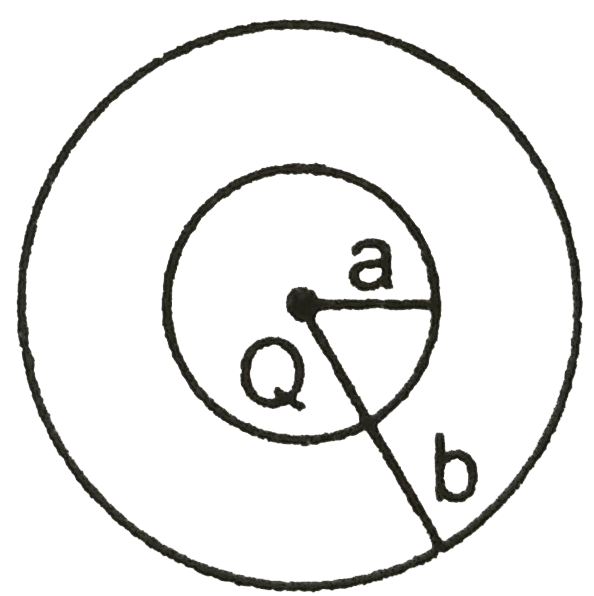
Reason : Mediating particle responsible for gravitational force is graviton.05:38View SolutionThe region between two concentric spheres of radii 'a' and 'b', respectively (see figure), have volume charge density rho=A/r , where A is a constant and r is the distance from the centre. At the centre of the spheres is a point charge Q. The value of A such that the electric field in the region between the spheres will be constant, is:
04:25View Solutionत्रिज्या a तथा b के दो संकेन्द्री गोले के बीच के स्थान में आयतन आवेश घनत्व ρ=A/r है जहाँ A स्थिरांक है तथा r केंद्र से दूरी है गोले के केंद्र पर एक बिंदु आवेश Q है A का वह मान बताये जिससे गोले के बीच के स्थान में एकसमान विधुत क्षेत्र हो
 03:27View Solution
03:27View SolutionA system consits of a uniformly charged sphere of radius R and a surrounding medium filled by a charge with the volume density rho=alpha/r , where alpha is a positive constant and r is the distance from the centre of the sphere. Find the charge of the sphere for which the electric field intensity E outside the sphere is independent of R.
06:40View SolutionAn insulating solid sphere of the radius R is charged in a non - uniform manner such that the volume charge density ρ=Ar, where A is a positive constant and r is the distance from the centre. The potential difference between the centre and surface of the sphere is
03:12View SolutionAn insulating solid sphere of the radius R is charged in a non - uniform manner such that the volume charge density ρ=Ar, where A is a positive constant and r is the distance from the centre. The potential difference between the centre and surface of the sphere is
02:19View SolutionCharge density of a sphere of radius R is rho = rho_0/r where r is distance from centre of sphere.Total charge of sphere will be
View SolutionThe region between two concentric spheres of radii 'a' and 'b', respectively (see figure), has volume charge density rho =A/r , where A is a constant and r is the distance from the centre. At the centre of the spheres is a point charge Q. The value of A such that the electric field in the region between the spheres will be constant is :
06:40View SolutionThe region between two concentric spheres of radii 'a' and 'b', respectively (see figure), have volume charge density ρ=Ar, where A is a constant and r is the distance from the centre. At the centre of the spheres is a point charge Q. The value of A such that the electric field in the region between the spheres will be constant, is:
 04:23View Solution
04:23View SolutionCharge density of a sphere of radius R is rho = rho_0/r where r is distance from centre of sphere.Total charge of sphere will be
04:43View SolutionA system consits of a uniformly charged sphere of radius R and a surrounding medium filled by a charge with the volume density ρ=αr, where α is a positive constant and r is the distance from the centre of the sphere. Find the charge of the sphere for which the electric field intensity E outside the sphere is independent of R.
05:19View Solution

