A system consits of a uniformly charged sphere of radius R and a surrounding medium filled by a charge with the volume density , where is a positive constant and r is the distance from the centre of the sphere. Find the charge of the sphere for which the electric field intensity E outside the sphere is independent of R.
None of these
The correct Answer is:C
Using Gauss theorem for spherical surface of radius r outside the sphere with a uniform charge density and a charge q
The intensity E does not depend on R if
Topper's Solved these Questions
- ELECTRIC CHARGES AND FIELDSBOOK - NCERT FINGERTIPSCHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - NCERT Exemplar
5 Videos
- ELECTRIC CHARGES AND FIELDSBOOK - NCERT FINGERTIPSCHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - EXEMPLAR PROBLEMS
1 Videos
- ELECTRIC CHARGES AND FIELDSBOOK - NCERT FINGERTIPSCHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - HOTS
1 Videos
- DUAL NATURE OF RADIATION AND MATTER BOOK - NCERT FINGERTIPSCHAPTER - DUAL NATURE OF RADIATION AND MATTER EXERCISE - Assertion And Reason
15 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - NCERT FINGERTIPSCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Assertion And Reason
15 Videos
Similar Questions
A system consists of a uniformly charged sphere of radius R and a surrounding by a medium with volume charge density ρ=ar, where α is a positive constant and r is the distance from the centre of the sphere. If NαR2 is the charge on the sphere when the electric field intensity outside the sphere is independent of r. What is the value of N ?
View SolutionA solid non conducting sphere of radius R has a non-uniform charge distribution of volume charge density, ρ=ρ0rR, where ρ0 is a constant and r is the distance from the centre of the sphere. Show that : (i) the total charge on the sphere is Q=πρ0R3 (ii) the electric field inside the sphere has a magnitude given by, E=KQr2R4
View Solution
Knowledge Check
An insulating solid sphere of the radius R is charged in a non - uniform manner such that the volume charge density ρ=Ar, where A is a positive constant and r is the distance from the centre. The potential difference between the centre and surface of the sphere is
AAR8ε0BAR4ε0CARε0DAR2ε0An insulating solid sphere of the radius R is charged in a non - uniform manner such that the volume charge density ρ=Ar, where A is a positive constant and r is the distance from the centre. The potential difference between the centre and surface of the sphere is
AAR8ε0BAR4ε0CARε0DAR2ε0The region between two concentric spheres of radii 'a' and 'b', respectively (see figure), have volume charge density ρ=Ar, where A is a constant and r is the distance from the centre. At the centre of the spheres is a point charge Q. The value of A such that the electric field in the region between the spheres will be constant, is:
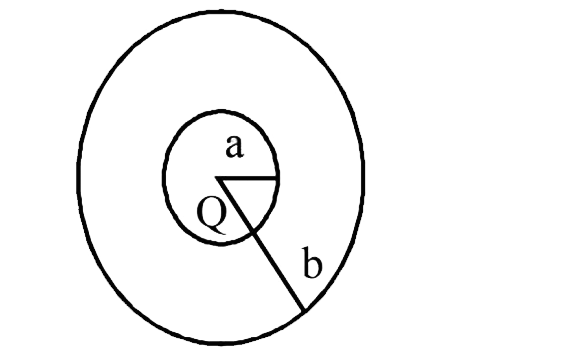 A(a) 2Qπ(a2−b2)B(b) 2Qπa2C(c) Q2πa2D(d) Q2π(b2−a2)
A(a) 2Qπ(a2−b2)B(b) 2Qπa2C(c) Q2πa2D(d) Q2π(b2−a2)
A solid non conducting sphere of radius R has a non-uniform charge distribution of volume charge density, ρ=ρ0rR, where ρ0 is a constant and r is the distance from the centre of the sphere. Show that : (i) the total charge on the sphere is Q=πρ0R3 (ii) the electric field inside the sphere has a magnitude given by, E=KQr2R4
View SolutionAn insulating solid sphere of the radius R is charged in a non - uniform manner such that the volume charge density ρ=Ar, where A is a positive constant and r is the distance from the centre. The potential difference between the centre and surface of the sphere is
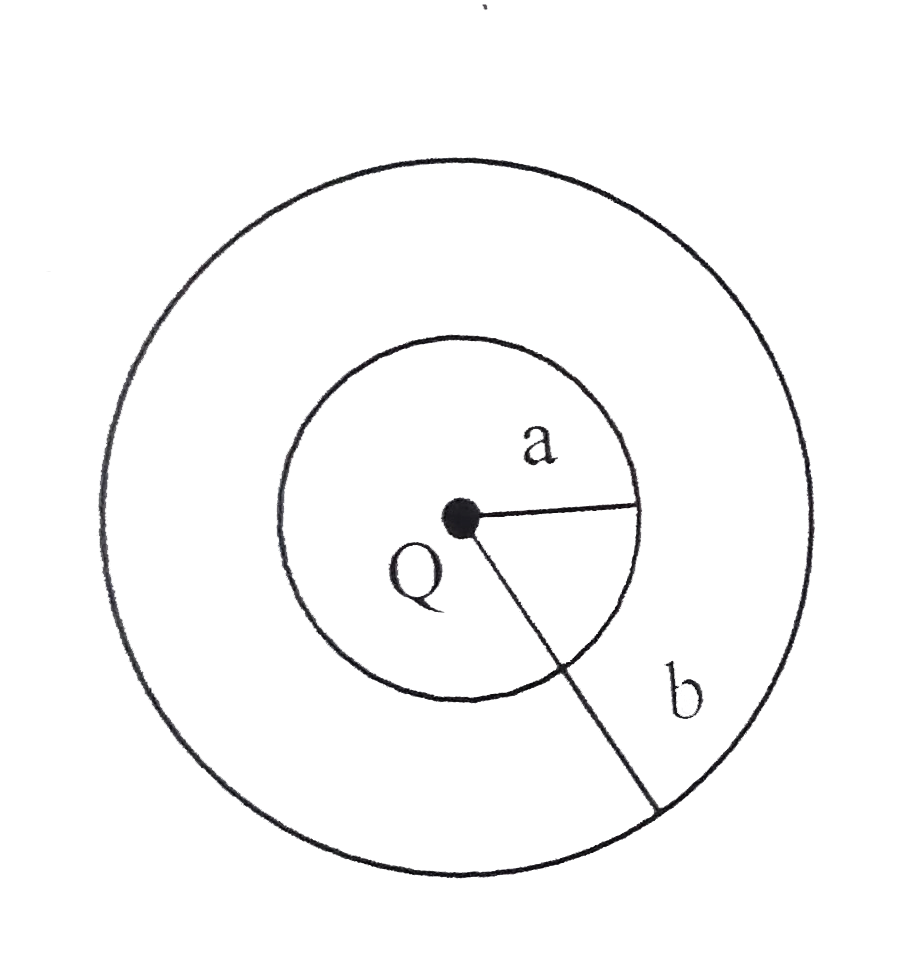
View SolutionThe region between two concentric spheres of radii 'a' and 'b', respectively (see figure), have volume charge density ρ=Ar, where A is a constant and r is the distance from the centre. At the centre of the spheres is a point charge Q. The value of A such that the electric field in the region between the spheres will be constant, is:

View SolutionThe region between two concentric spheres of radii ‘a’ and ‘b’, respectively (see figure), has volume charge density p=Ar, where A is a constant and r is the distance from the centre. At the centre of the spheres is a point charge Q. The value of A such that the electric field in the region between the spheres will be constant, is :
View SolutionA solid sphere of radius R has a charge Q distributed in its volume with a charge density ρ=kra, where k and a are constants and r is the distance from its centre. If the electric field at r=R2 is 18 times that r=R, find the value of a.
View Solution
