A rod has non uniform mass distribution. The mass increases uniformly from left end (A) to right end (B). It is most difficult to rotate the rod about as axis
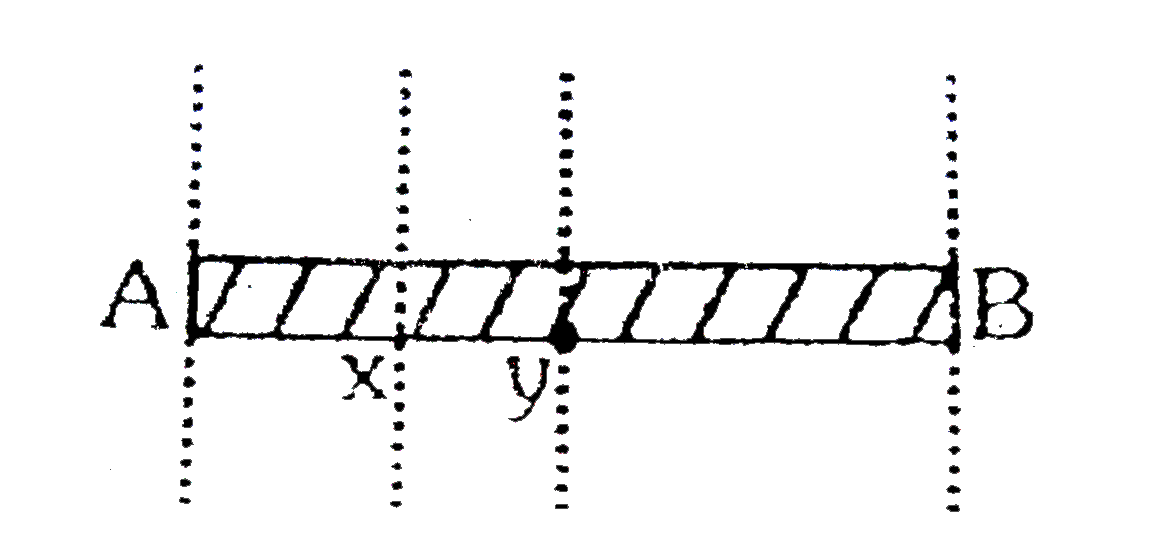 Solution in Gujrati
Solution in Gujrati
Passing through A
Passing through B
Passing x
Passing y
The correct Answer is:A
M.I. is greatest about axis through A.
Topper's Solved these Questions
- TEST PAPERBOOK - ALLEN CHAPTER - TEST PAPEREXERCISE - PHYSICS
4 Videos
- TEST PAPERBOOK - ALLEN CHAPTER - TEST PAPEREXERCISE - PHYSICS
4 Videos
- SIMPLE HARMONIC MOTIONBOOK - ALLEN CHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Example
1 Videos
- TEST PAPER 1BOOK - ALLEN CHAPTER - TEST PAPER 1EXERCISE - PHYSICS
11 Videos
Similar Questions
Choose the correct statement:
View SolutionChoose the correct statement:
View SolutionA rod with rectangular cross section oscillates about a horizontal axis passing through one of its ends and it behaves like a seconds pendulum, its length will be
View SolutionWhy are electric field lines perpendicular at a point on an equipotential surface of a conductor ?
View SolutionA uniform rod of mass 300 g and length 50 cm rotates at a uniform asngulr speed of 2 rad/s about an axis perpendicular to the rod through an end. Calculte a. the angular momentum of the rod about the axis of rotation b. the speed of thecentre of the rod and c. its kinetic energy.
View SolutionA rod of uniform cross-section of mass M and length L is hinged about an end to swing freely in a vertical plane. Howerver, its density is non uniform and varies linearly from hinged end to the free end doubling its value. The moment of inertia of the rod, about the rotation axis passing through the hinge point
View SolutionA conical pendulum, a thin uniform rod of length l and mass m , rotates uniformly about a vertical axis with angular velocity omega (the upper end of the rod is hinged). Find the angle theta between the rod and the vertical.
View SolutionA thin uniform copper rod of length l and mass m rotates uniformly with an angular velocity omega in a horizontal plane about a vertical axis passing through one of its ends. Determine the tension in the rod as a function of the distance r from the rotation axis. Find the elongation of the rod.
View SolutionTwo point masses A of mass M and B of mass of 4M are fixed at the ends of a rod of length l and of negligible mass. The rod is set rotation about an axis perpendicular to its length with a uniform angular speed. The work required for rotating the rod will be minimum when the distance of axis of rotation from the mass A is at
View SolutionA thin uniform rod is free to rotate about a fixed smooth horizontal axis as shown. A point mass hits horizontally with velocity v_(0) to the one end B of the rod. When it hits, it sticks to the rod, then :
View SolutionA uniform rod AB of mass m and length L rotates about a fixed vertical axis making a constant angle theta with it as shown in figure. The rod is rotated about this axis, so that point B the free end of the rod moves with a uniform speed V in the horizontal plane then the angular momentum of the rod about the axis is:
View SolutionA uniform rod of mass m and length L is fixed to an axis, making an angle θ with it as shown in the figure. The rod is rotated about this axis so that the free end of the rod moves with a uniform speed ‘v’. Find the angular momentum of the rod about the axis. Is the angular momentum of the rod about point A constant?
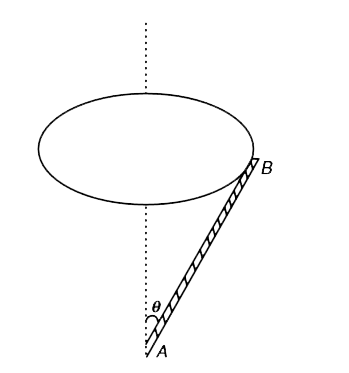
View SolutionA thin uniform copper rod of length l and cross-section area A and mass m rotates uniformly with an angular velocity omega in a horizontal plane about a vertical axis passing through one of its ends. The elongation of the rod will be
View SolutionThe mass per unit length of a non-uniform rod of length L is given by mu= lamdaxx2 , where lamda is a constant and x is distance from one end of the rod. The distance of the center of mass of rod from this end is :-
View SolutionThe mass per unit length of a non-uniform rod of length L is given by μ=λx2, where λ is constant and x is distance from one end of the rod. The distance of the center of mass of rod from this end is
View SolutionFigure shows a thin, uniform rod of mass M and length L, on an x axis with the origin at the rod's center. (a) What is the rotational inertia of the rod about the perpendicular rotation axis through the center? (b) What is the rod's rotational inertia I about a new rotation axis that is perpendicular to the rod and through the left end?
View Solution
