A solid hemisphere and a hemisphereical shell are joined as shown. Both of them has mass m/2 individually. Find out moment of inertia about axis I1,I2.
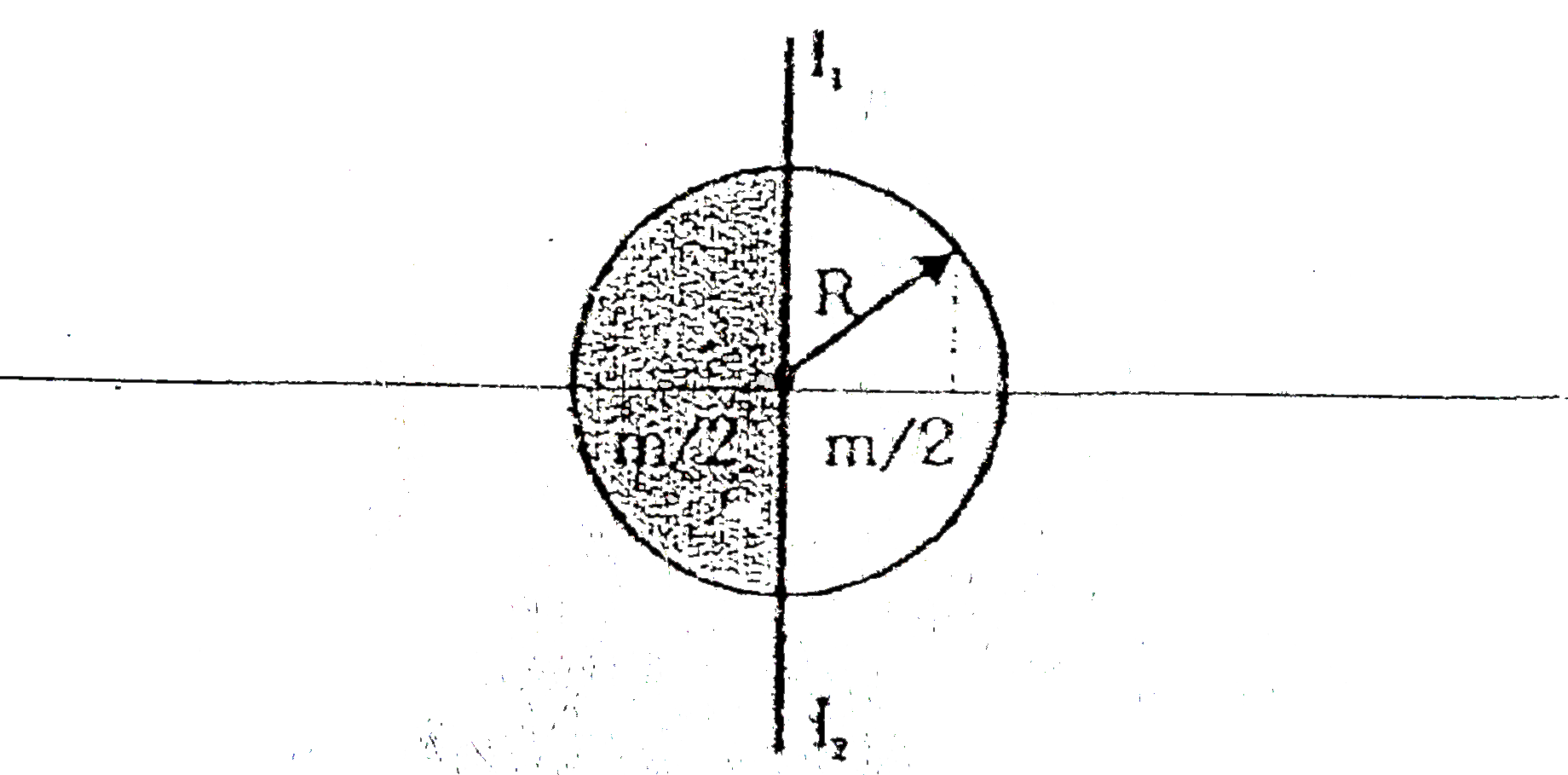 Solution in Gujrati
Solution in Gujrati
8mR215
27mR2
25mR2
23mR2
The correct Answer is:A
25(m2)R2+23(m2)R2=8mR215
Topper's Solved these Questions
- TEST PAPERBOOK - ALLEN CHAPTER - TEST PAPEREXERCISE - PHYSICS
4 Videos
- TEST PAPERBOOK - ALLEN CHAPTER - TEST PAPEREXERCISE - PHYSICS
4 Videos
- SIMPLE HARMONIC MOTIONBOOK - ALLEN CHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Example
1 Videos
- TEST PAPER 1BOOK - ALLEN CHAPTER - TEST PAPER 1EXERCISE - PHYSICS
11 Videos
Similar Questions
Choose the correct statement:
View SolutionChoose the correct statement:
View SolutionA rod with rectangular cross section oscillates about a horizontal axis passing through one of its ends and it behaves like a seconds pendulum, its length will be
View SolutionWhy are electric field lines perpendicular at a point on an equipotential surface of a conductor ?
View SolutionA solid sphere of mass m& rdius R is divided in two parts of m mass 7m8&m8, and converted to a disc of radius 2R& solid sphere of radius 'r' respectively. Find I1I2 , If I1&I2 are moment of inertia of disc & solid sphere respectively
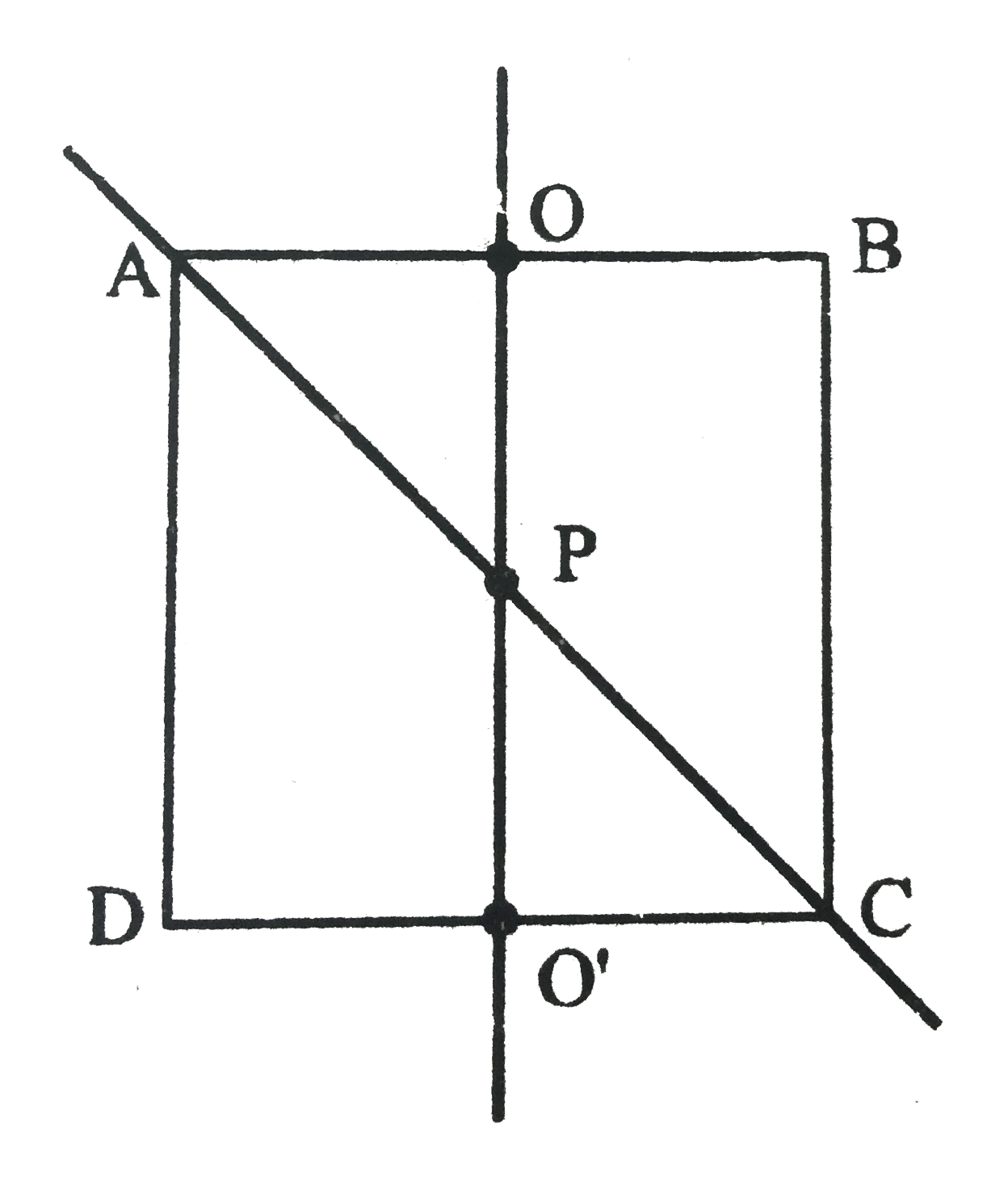
View SolutionLet I_(1) and I_(2) be the moment of inertia of a uniform square plate about axes shown in the figure. Then the ratio I_(1):I_(2) is
View SolutionLet I1 and I2 be the moment of inertia of a uniform square plate about axes APC and OPO respectively as shown in the figure.P is centre of square. The ratio I1I2 moment of inertia is -
 .
.
View SolutionThe moment of inertia of a uniform rod about a perpendicular axis passing through one end is I_(1) . The same rod is bent into a ring and its moment of inertia about a diameter is I_(2) . Then I_(1)//I_(2) is
View SolutionFind the moment of inertia of a hemisphere of mass M and radius R shown in the figure, about an axis A A' tangential to the hemisphere.
View SolutionA semi-circular ring has mass m and radius R as shown in figure. Let I_(1),I_(2) ,I_(3) " and "I_(4) be the moments of inertia about the four axes as shown . Axis 1 passes through centre and is perpendicular to plane of ring. Then , match the following.
View SolutionIf I_(1),I_(2) and I_(3) are the moments of inertia about the natural axies of solid sphere, hollow sphere and a spherical shell of same mass and radii, the correct result of the following is
View SolutionIf I1 is the moment of inertia of a thin rod about an axis perpendicular to its length and passing through its centre of mass, and I2 is the moment of inertia (about central axis) of the ring formed by bending the rod, then
View SolutionA solid sphere of mass M and radius R is divided into two unequal parts. The first parts has a mass of 7M8 and is converted into a uniform disc of radius 2R. The second part is converted into a uniform solid sphere. Let I1 be the moment of inertia of the uniform disc about its axis and I2 be the moment of inertia of the sphere made from remaining part about its axis. The ratio I1/I2 is 140x. Find the value of x.
View SolutionA solid sphere of mass m& rdius R is divided in two parts of m mass 7m8&m8, and converted to a disc of radius 2R& solid sphere of radius 'r' respectively. Find I1I2 , If I1&I2 are moment of inertia of disc & solid sphere respectively
View SolutionA solid sphere of mass m& rdius R is divided in two parts of m mass 7m8&m8, and converted to a disc of radius 2R& solid sphere of radius 'r' respectively. Find I1I2 , If I1&I2 are moment of inertia of disc & solid sphere respectively
View SolutionA solid sphere of mass m& rdius R is divided in two parts of m mass 7m8&m8, and converted to a disc of radius 2R& solid sphere of radius 'r' respectively. Find I1I2 , If I1&I2 are moment of inertia of disc & solid sphere respectively
View Solution
