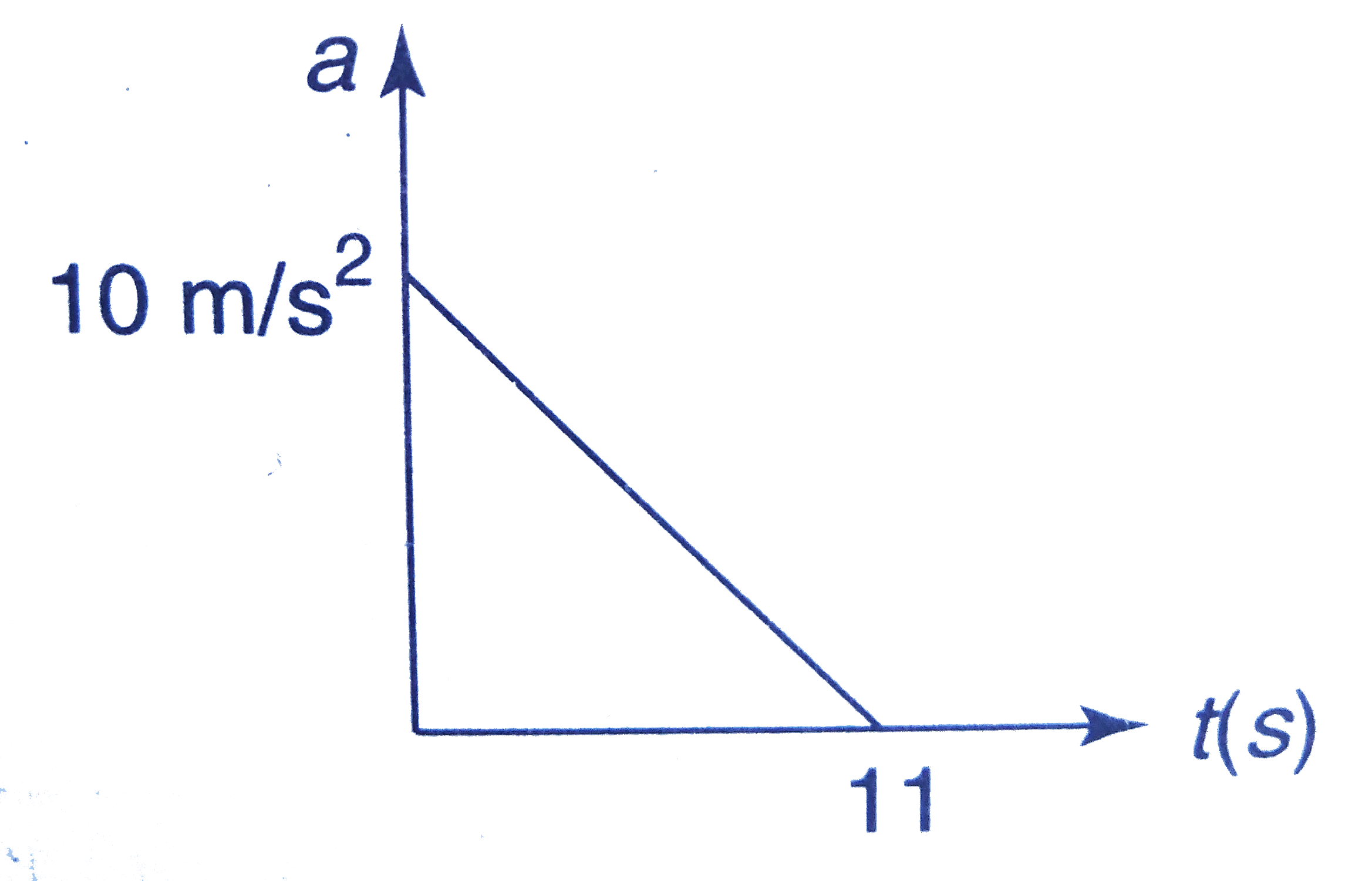
A particle starting from rest. Its acceleration (a) versus time (t) is as shown in the figure.
The maximum speed of the particle will be.
 Solution in Gujrati
Solution in Gujrati
110m/s
55m/s
550m/s
660m/s
The correct Answer is:B
a=−1011t+10 at maximum speed a=0
1011t+10
⇒t=11 sec
Area under the curve=12×11×10=55
Topper's Solved these Questions
- KINEMATICSBOOK - ALLEN CHAPTER - KINEMATICSEXERCISE - MCQ with one or more than one correct Question
1 Videos
- KINEMATICSBOOK - ALLEN CHAPTER - KINEMATICSEXERCISE - SUBJECTIVE QUESTION
3 Videos
- KINEMATICSBOOK - ALLEN CHAPTER - KINEMATICSEXERCISE - Exercise-05 [A]
11 Videos
- ERROR AND MEASUREMENTBOOK - ALLEN CHAPTER - ERROR AND MEASUREMENTEXERCISE - Part-2(Exercise-2)(B)
22 Videos
- KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)BOOK - ALLEN CHAPTER - KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)EXERCISE - BEGINNER S BOX-7
8 Videos
Similar Questions
The coordinate of a particle moving in a plane are given by x(t)=acos(pt)andy(t)=bsin(pt) where a,b(<a) and P are positive constants of appropriate dimensions . Then
View SolutionA large heavy box is sliding without friction down a smooth plane of inclination θ. From a point P on the bottom of the box, a particle is projected inside the box. The initial speed of the particle with respect to box is u and the direction of projection makes an angle α with the bottom as shown in figure.

(i) Find the distance along the bottom of the box between the point of projection P and the point Q where the particle lands. (Assume that the particle does not hit any other surface of the box. Neglect air resistance).
(ii) If the horizontal displacement of the particle as seen by an observer on the ground is zero, find the speed of the box with respect to the ground at the instant when the particle was projected.
View SolutionA ball whose kinetic energy is E , is projected at an angle of 45∘ to the horizontal . The kinetic energy of the ball at the highest point of its flight will be
View SolutionA cube has a side of length 1.2×10−2m. Calculate its volume.
View SolutionA football player kicks a ball at an angle of 30∘ with an initial speed of 20 m/s. Assuming that the ball travels in a vertical plane, calculate (a) the time at which the ball reaches the highest point (b) the maximum height reached (c) the horizontal range of the ball (d) the time for which the ball is in the air, (g=10m/s2)
View SolutionA particle starting from rest. Its acceleration (a) versus time (t) is as shown in the figure.
The maximum speed of the particle will be.

View SolutionFigure shows the graph of acceleration of particle as a function of time. The maximum speed of the particle is (particle starts from rest).
View SolutionThe acceleration versus time graph for a particle moving along a straight line is shown in the figure. If the particle starts from rest at t = 0, then its speed at t = 30 sec will be :
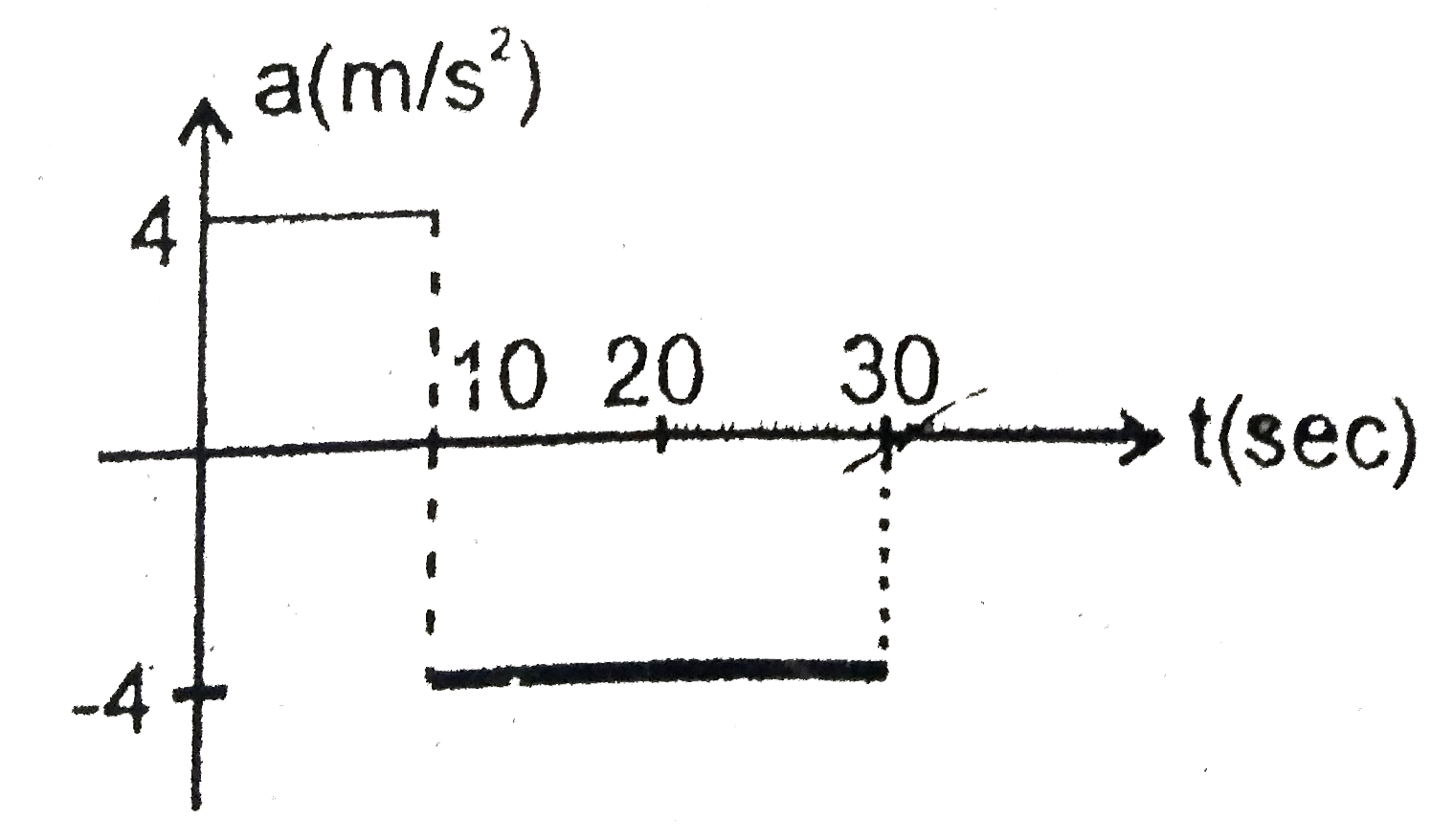
View SolutionA particle starts moving from rest in a from rest in a straight line. Its acceleration vs time (a - t) graph is shown in figure. The speed of particle is maximum at.
View SolutionA particle starts moving from rest on a straight line. Its acceleration a verses time t is shown in the figure. The speed of the particle is maximum at the instant
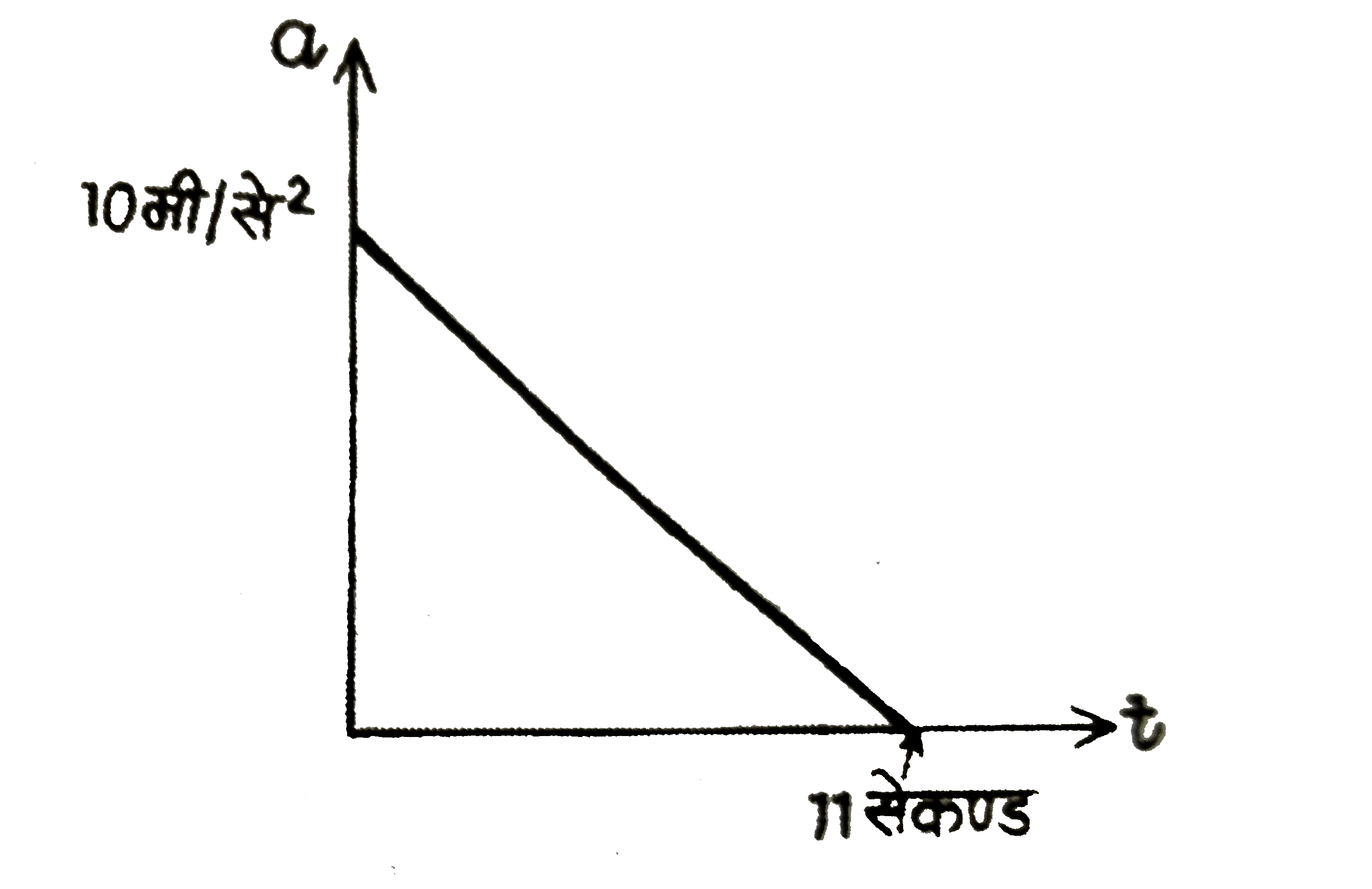
View Solutionएक कण विरामावस्था से चलना प्रारम्भ करता है । इसका त्वरण (a) , समय (t) ग्राफ संलग्न चित्र में दिखाया गया है । कण द्वारा अर्जित अधिकतम चाल है :
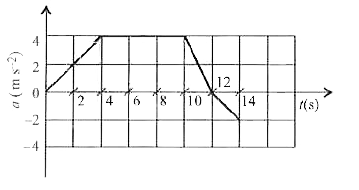
View SolutionA graph of acceleration versus time of a particle starting from rest at t=0 is as shown in figure. The speed of the particle at t = 14s is
View SolutionA particle stars from rest. Its acceleration (a) versus time (t) is as shown in the figure . The maximum speed of the particle will be:
View SolutionA graph of acceleration versus time of a particle starting from rest at t =0 is shown. The speed of the particle at t=14 second is
View SolutionA particle starts from rest. Its acceleration (a) versus time (t) is as shown in the figure. The maximum speed of the particle will be
View SolutionA particle starts from rest .its acceleration a versus time t is as shown in the figure . Find the maximum speed of the particle during its motion
(a is in ms−2and t is in seconds)
View Solution
