Assuming the length of a chain to be L and coefficient of static friction μ. Compute the maximum length of the chain which can be held outside a table without sliding. Solution in Gujrati
Let y be the maximum length of the chain can be hold out side the table without sliding.
Length of chain on the table =(L−y)
Weight of part of the chain on table W'=ML(L−y)g
Weight of hanging part of the chain W=MLyg
For equilibrium: limiting force of friction=weight of hanging part of the chain
μR=W⇒μW=W⇒μML(L−y)g=MLyg⇒μL−μy=y⇒y=μL1+μ

Topper's Solved these Questions
- NEWTONS LAWS OF MOTIONBOOK - ALLEN CHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - EXERCISE-I
52 Videos
- NEWTONS LAWS OF MOTIONBOOK - ALLEN CHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - EXERCISE-II
112 Videos
- NEWTONS LAWS OF MOTIONBOOK - ALLEN CHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - EXERCISE-III
28 Videos
- NEWTON'S LAWS OF MOTION & FRICTIONBOOK - ALLEN CHAPTER - NEWTON'S LAWS OF MOTION & FRICTIONEXERCISE - EXERCISE (JA)
4 Videos
- RACEBOOK - ALLEN CHAPTER - RACEEXERCISE - Basic Maths (Wave Motion & Dopplers Effect) (Stationary waves & doppler effect, beats)
25 Videos
Similar Questions
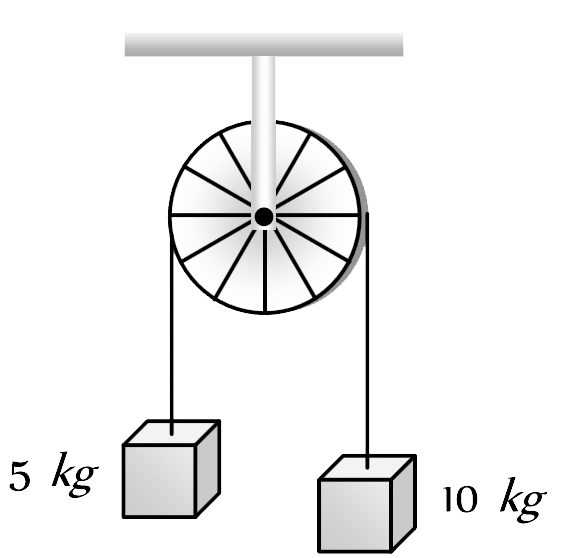
USS 150) Two masses of 5 kg and 10 kg are connected to a pulley as shown. What will be the acceleration of the system (g= acceleration due to gravity)
View SolutionA particle is in straight line motion with uniform velocity A force is not required
View SolutionAssertion: The driver in a vechicle moving with a constant speed on a straight road is in a non-inertial frame of referance.
Reason: A reference frame in which Newton's laws of motion are applicable is non-inertial.
View SolutionA piece of wire is bent in the shape of a parabola y=kx2 (y-axis vertical) with a bead of mass m on it. The bead can slide on the wire without friction. It stays at the lowest point of the parabola when the wire is at rest. The wire is now accelerated parallel to the x-axis with a constant acceleration a. The distance of the new equilibrium position of the bead, where the bead can stay at rest with respect to the wire, from the y-axis is:
View SolutionThe frequency of a radar is 780 MHz. After getting reflected from an approaching aeroplane, the apparent frequency is more than the actual frequency by 2.6 kHz. The aeroplane has a speed of
View SolutionChain of mass M length L kept on rough sphere. mu is coefficient if friction between sphere and chain F is minimum force required to slide chain
View SolutionA homogeneous chain of length L lie on a table. If the coefficent of friction is mu , find the maximum length L_(1) of the chain which can hang from the edge of the table without the chain sliding down. (b) Consider the situation as shown in the figure. Find teh minimum value of m so that the blocks do not move.
View SolutionA homogoneous chain of length L lies on a table. The coefficient of friction between the chain and the table is μ. The maximum length which can hang over the table in equilibrium is
View SolutionA uniform rope of length l lies on a table. If the coefficient of friction is μ, then the maximum length L of the part of this rope which can overhang from the edge of the table without sliding down is
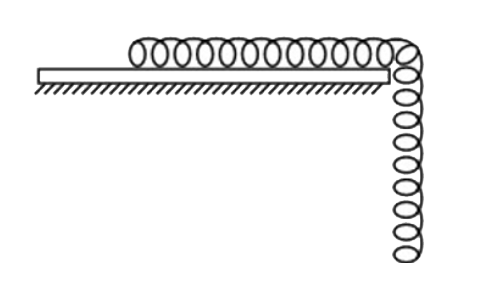
View SolutionA chain is placed on a rough table, partially hanging, as shown in the figure. The coefficient of static friction between the chain and the table is μ = 0.4. If the maximum possible length of the hanging part is x and the length of the chain is L, then what is the value of Lx?
View SolutionA uniform chain of length L hangs partially from table and held in equilibrium by friction. If greatest length of chain that hangs without slipping is l then the coefficient of friction between chain and table is
View SolutionA uniform chain of length L is lying on the horizontal table.If the coefficient of friction between the chain and table top is m, what is the maximum length of the chain that can hang over the edge of the table without disturbing the rest of the chain on the table?
View SolutionA chain is placed on a rough table, partially hanging, as shown in the figure. The coefficient of static friction between the chain and the table is μ = 0.4. If the maximum possible length of the hanging part is x and the length of the chain is L, then what is the value of Lx?

View SolutionL लम्बाई की एक समान रस्सी मेज पर रखी है। यदि घर्षण गुणांक μ है तो रस्सी की अधिकतम लम्बाई जो बिना नीचे फिसले मेज के एक किनारे से लटक सकती है
View SolutionL लम्बाई तथा M द्रव्यमान की समान चेन को क्षैतिज टेबल पर लटकाया गया है जिसका 23 भाग टेबल पर है। यदि टेबल व चेन के मध्य घर्षण गुणांक μ है तो चेन द्वारा टेबल से फिसलने के समय घर्षण द्वारा किया गया कार्य होगा
View SolutionPart of a uniform chain of length L is hanging out of a table. If the coefficient of friction between the chain and the table is , mu estimate the maximum length of the chain that can hang without slipping.
View Solution
