If the coefficient of friction between an insect and bowl is μ and the radius of the bowl is r, find the maximum height to which the insect can crawl in the bowl.Solution in Gujrati
The insect will crawl up the bowl till the component of its weight along the bowl is balanced by limiting fricitional force, So, resolving weight perpendiuclar to the bowl and along the bowl,
N=mgcosθ,tL=mgsinθ⇒tanθ=fN⇒tanθ=μ[∵fL=μN]
⇒√(r2−y2y)=μ⇒y=r√1+u2 So h=r−y=r[1−1√1+μ2]

Topper's Solved these Questions
- NEWTONS LAWS OF MOTIONBOOK - ALLEN CHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - EXERCISE-I
52 Videos
- NEWTONS LAWS OF MOTIONBOOK - ALLEN CHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - EXERCISE-II
112 Videos
- NEWTONS LAWS OF MOTIONBOOK - ALLEN CHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - EXERCISE-III
28 Videos
- NEWTON'S LAWS OF MOTION & FRICTIONBOOK - ALLEN CHAPTER - NEWTON'S LAWS OF MOTION & FRICTIONEXERCISE - EXERCISE (JA)
4 Videos
- RACEBOOK - ALLEN CHAPTER - RACEEXERCISE - Basic Maths (Wave Motion & Dopplers Effect) (Stationary waves & doppler effect, beats)
25 Videos
Similar Questions
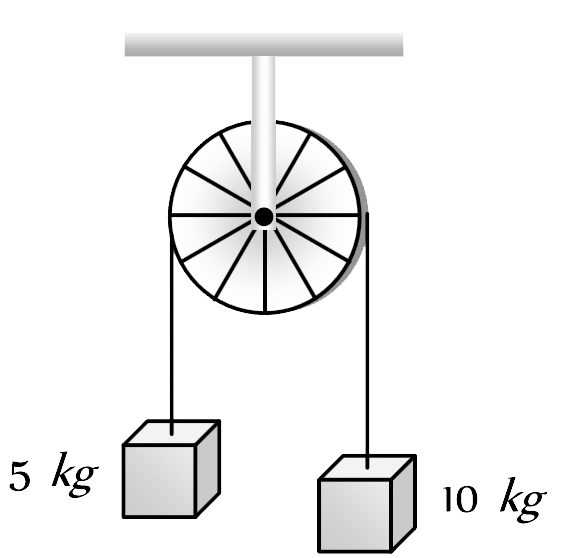
USS 150) Two masses of 5 kg and 10 kg are connected to a pulley as shown. What will be the acceleration of the system (g= acceleration due to gravity)
View SolutionA particle is in straight line motion with uniform velocity A force is not required
View SolutionAssertion: The driver in a vechicle moving with a constant speed on a straight road is in a non-inertial frame of referance.
Reason: A reference frame in which Newton's laws of motion are applicable is non-inertial.
View SolutionA piece of wire is bent in the shape of a parabola y=kx2 (y-axis vertical) with a bead of mass m on it. The bead can slide on the wire without friction. It stays at the lowest point of the parabola when the wire is at rest. The wire is now accelerated parallel to the x-axis with a constant acceleration a. The distance of the new equilibrium position of the bead, where the bead can stay at rest with respect to the wire, from the y-axis is:
View SolutionThe frequency of a radar is 780 MHz. After getting reflected from an approaching aeroplane, the apparent frequency is more than the actual frequency by 2.6 kHz. The aeroplane has a speed of
View SolutionA hemispherical bowl is made of steel, 0.25 cm thick. The inner radius of the bowl is5 cm. Find the outer curved surface area of the bowl.
View SolutionA hemispherical bowl of radius R is set rotating about its axis of symmetry which is kept vertical. A small block kept in the bowl rotates with the bowl without slipping on its surface. If the surfaces of the bowl is smooth, and the angle made by the radius through the block with the vertical is θ, find the angular speed at which the bowl is rotating.
View SolutionCalculate the height upto which an insect can crawl up a fixed bowl in the from of a hemisphere of radius r Given coefficient of friction = 1 sqrt(3) .
View SolutionA hemispherical bowl of uniform mass distribution of mass ‘M’ is at rest on frictionless horizontal ground sur- face. There is a small insect of mass 'm' on bowl at point ‘A’ of the bowl at rest. Now the insect moves with constant speed ‘v’ relative to bowl in vertical plane. Assume that insect does not slip on the bowl. When the insect reaches point ‘P’ of the hemisphere the displacement of hemisphere w.r.t. ground is :
View SolutionA hemispherical bowl of uniform mass distribution of mass ‘M’ is at rest on frictionless horizontal ground sur- face. There is a small insect of mass 'm' on bowl at point ‘A’ of the bowl at rest. Now the insect moves with constant speed ‘v’ relative to bowl in vertical plane. Assume that insect does not slip on the bowl.

When the insect is at point ‘P’ of the hemispherical bowl the acceleration of bowl is :
View SolutionA hemispherical bowl of uniform mass distribution of mass ‘M’ is at rest on frictionless horizontal ground sur- face. There is a small insect of mass 'm' on bowl at point ‘A’ of the bowl at rest. Now the insect moves with constant speed ‘v’ relative to bowl in vertical plane. Assume that insect does not slip on the bowl.
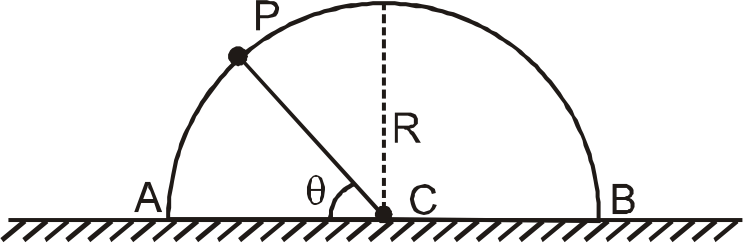
When insect at point ‘P’ on the bowl the displacement of centre of mass of the system (bowl + insect) is :
View SolutionThe coefficient of friction between a hemispherical bowl and an insect is sqrt(0.44) and the radius of the bowl is 0.6m . The maximum height to which an insect can crawl in the bowl will be .
View SolutionA small insect is climbing slowly along the inner wall of a hemispherical bowl of radius R. The insect is unable to climb beyond theta = 45^(@) . Whenever it tries to climb beyond theta = 45^(@) , it slips. (a) Find the minimum angular speed omega with which the bowl shall be rotated about its vertical radius so that the insect can climb upto theta = 60^(@) . (b) Find minimum omega for which the insect can move out of the bowl.
View SolutionCalculate the height upto which an insect can crawl up a fixed bowl in the form of a hemisphere of radius r. Given coefficient of friction is 1/√3.
View SolutionThe coefficient of friction between an insect and a hemispherical bowl of radius r is mu . The maximum height to which the insect can crawl in the bowl is
View SolutionThe coefficient of friction between a hemispherical bowl and an insect is √0.44 and the radius of the bowl is 0.6m. The maximum height to which an insect can crawl in the bowl will be
View Solution
