Question

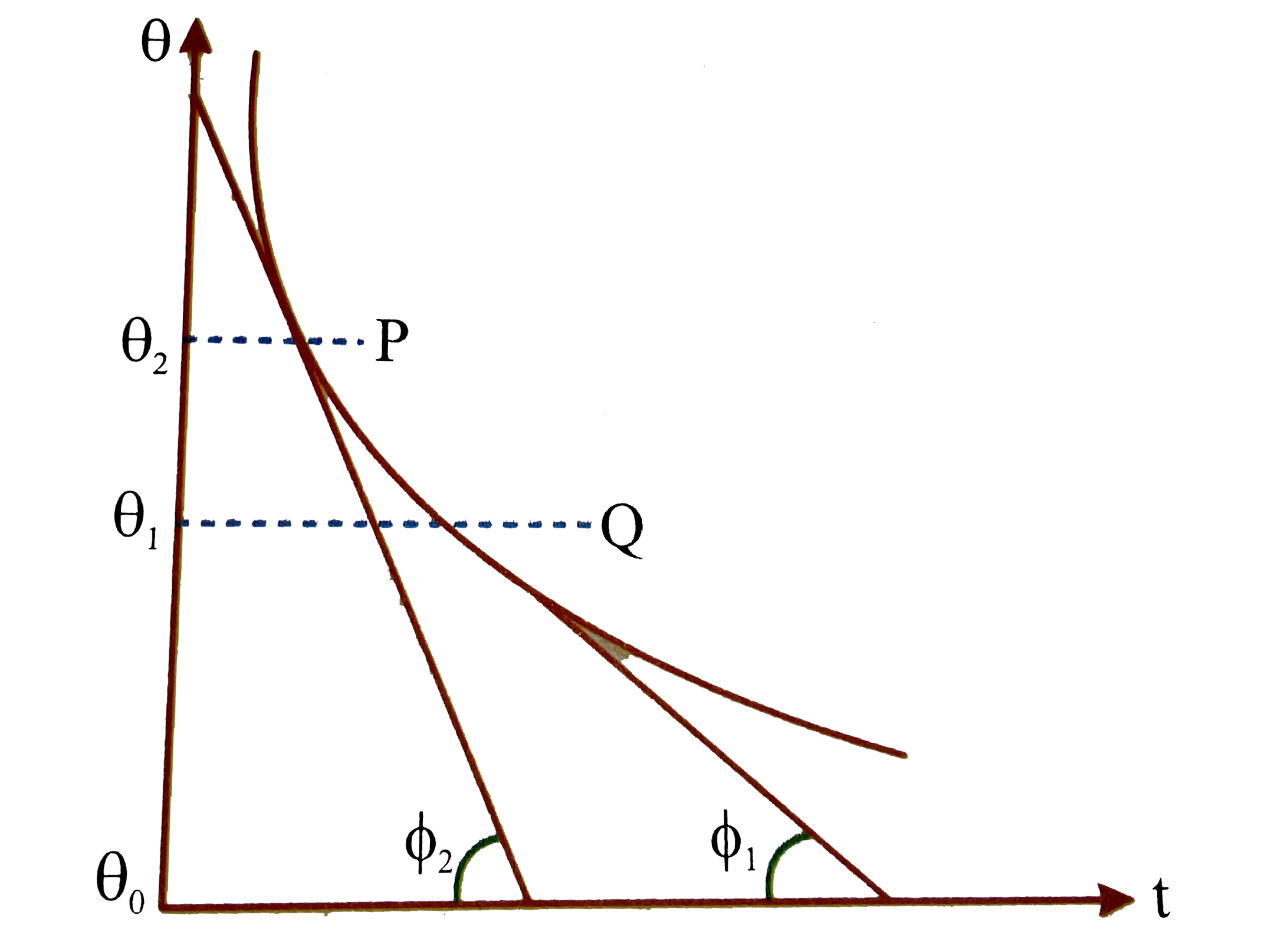
A body cools in a surrounding which is at constant temperature of ${\theta }_0$. Assume that it obeys Newton's law of colling. Its temperature $\theta$ is plotted against time $t$. Tangents are drawn to the curve at the points $P(\theta ={\theta }_t)$ and $Q(\theta ={\theta }_2)$. These tangents meet the time axis at angles of ${\varphi }_2$ and ${\varphi }_1$, as shown

Options

A. `(tanphi_(2))/(tanphi_(1)) = (theta_(1)-theta_(0))/(theta_(2)-theta_(0))`
B. `(tanphi_(2))/(tanphi_(1)) = (theta_(2)-theta_(0))/(theta_(1)-theta_(0))`
C. `(tanphi_(1))/(tanphi_(2)) = (theta_(1))/(theta_(2))`
D. `(tanphi_(1))/(tanphi_(2)) = (theta_(2))/(theta_(1))`

Answer

B

Explanation

Newton's law of cooling implies that rate of cooling is proportional to temperature difference if the temperature difference between body and surrounding is small.
Then , `(-(d theta)/(dt))_(2) = tanphi_(2)alpha(theta_(2)-theta_(0))` and
`((d theta)/(dt))_(1) = tanphi_(1)alpha(theta_(1) -theta_(0)) implies (tanphi_(2))/(tanphi_(1)) = ((theta_(2)-theta_(0))/(theta_(1) - theta_(0)))`