One end of a rod of length L and cross - sectioal area A is kept in a furance of temperature T1 . The other end of the rod is kept at a tempearute T2 . The thermal conducitivity of the material of the rod is K and emissivity of rod is K and emissivity of rod is e. It is given that T2=Ts+ΔT, where ΔT<<Ts,Ts being the temperature of surroudings. If ΔT∝(T1−Ts) , find the proportionality constant. Consider that heat is lost only by radiation at the end where the temperature of the rod is T2..
Rate of Heat gained by rod through conduction , Q=KA(T1−T2)L

Rate of Heat lost by rod through radiation , Q2=eAσ(T42−T4s)
In steady state Q1=Q2
∴KA(T1−T2)L=eAσ(T42−T4s)..........(1)
Given T2=Ts+ΔT ∴T42=(Ts+ΔT)4=T4S+(1+ΔTTs)4
As ΔT<<Ts , so using bionmial theorem .
T42=T4s(1+4ΔTTs)⇒T42−T4s=4T3sΔT
substituting this value in (1) , we get KA(T1−T2)L=eAσ.(4T3sΔT) Also T2=Ts+ΔT
∴KA(T1−Ts−ΔT)L=eAσ(4T3sΔT)⇒K(T1−Ts)L−KLΔT=4eσT3sΔT
(or) K(T1−Ts)L=(4eσT3s+KL)ΔT,ΔT=K(T1−TS)(4eσLT3s+K) But given ΔT=C(T1−Ts)
∴ Constant of proportioanlity C is KK+4eσLT3s
Topper's Solved these Questions
- TRANSMISSION OF HEAT BOOK - AAKASH SERIESCHAPTER - TRANSMISSION OF HEAT EXERCISE - TEST YOUR SELF
6 Videos
- TRANSMISSION OF HEAT BOOK - AAKASH SERIESCHAPTER - TRANSMISSION OF HEAT EXERCISE - VERY SHORT ANSWER TYPE QUESTIONS
28 Videos
- THERMOMETRY BOOK - AAKASH SERIESCHAPTER - THERMOMETRY EXERCISE - Numerical Exercise (LEVEL- 1)
11 Videos
- TRANSMISSION OF HEATBOOK - AAKASH SERIESCHAPTER - TRANSMISSION OF HEATEXERCISE - ADDITIONAL PRACTICE EXERCISE (PRACTICE SHEET (ADVANCED)) (Integer/Subjective Type Questions)
3 Videos
Similar Questions
One end of rod of length L and cross-sectional area A is kept in a furance of temperature T1. The other end of the rod is kept at at temperature T2. The thermal conductivity of the material of the rod is K and emissivity of the rod is e. It is given that T2=TS+ΔT where ΔT<<TS, TS being the temperature of the surroundings. If ΔT∝(T1−TS), find the proportionality constant. Consider that heat is lost only by radiation at the end where the temperature of the rod is T2.
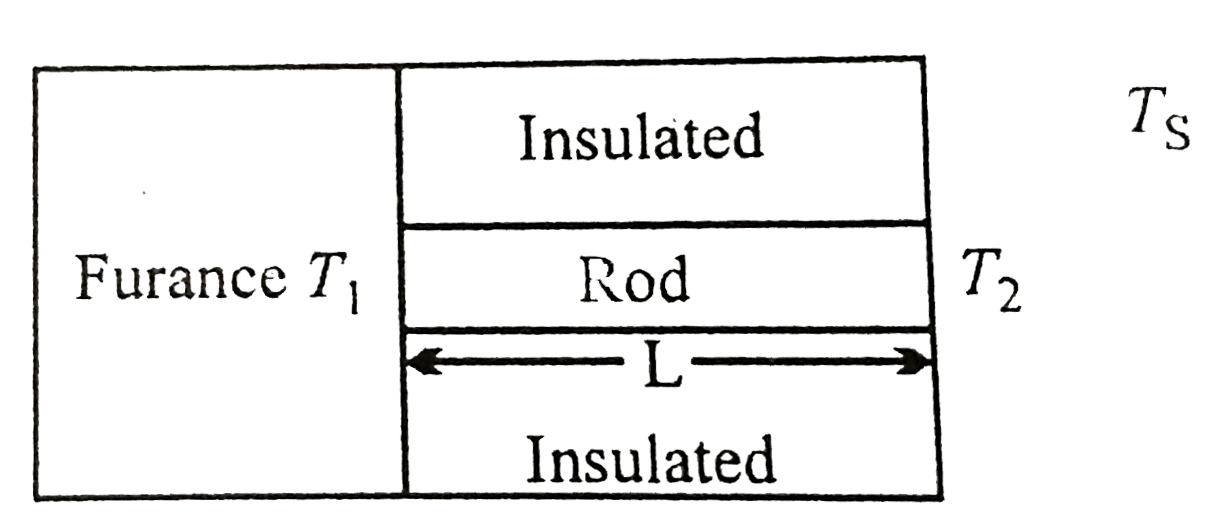
View SolutionOne end of rod of length L and cross-sectional area A is kept in a furance of temperature T1. The other end of the rod is kept at at temperature T2. The thermal conductivity of the material of the rod is K and emissivity of the rod is e. It is given that T2=TS+ΔT where ΔT<<TS, TS being the temperature of the surroundings. If ΔT∝(T1−TS), find the proportionality constant. Consider that heat is lost only by radiation at the end where the temperature of the rod is T2.

View Solution
Knowledge Check
One end of a metal rod is kept in a furnce. In steady state, the temperature of the rod
AincreasesBdecreasesCremains constantDis non uniform.The two ends of a rod of length L and a uniform cross-sectional area A are kept at two temperature T1 and T2 (T1>T2). The rate of heat transfer. dQdt, through the rod in a steady state is given by
AdQdt=KL(T1−T2)ABdQdt=KL(T1−T2)LACdQdt=KLA(T1−T2)DdQdt=KA(T1−T2)LA metal rod of area of cross section A has length L and coefficient of thermal conductivity K the thermal resistance of the rod is .
ALKABKLLCKALDAKL
One end of a rod of length L and crosssectional area A is kept in a furnace at temperature T1. The other end of the rod is kept at a temperature T2. The thermal conductivity of the matrieal of the rod is K and emissivity of the rod is e. It is gives that T!=Ts+ΔT, where ΔT<<Ts,Ts is the temperature of the surroundings. If ΔT∝(T1−T2) find the proportional constant, consider that heat is lost only by rediation at the end where the temperature of the rod is T1.

View SolutionOne end of a metal rod is kept in a furnace. In steady state, the temperature of the rod
View SolutionOne end of a metal rod is kept in a furnace. In steady state, the temperature of the rod
View SolutionThe two ends of a rod of length L and a uniform cross-sectional area A are kept at two temperature T1 and T2 (T1>T2). The rate of heat transfer. dQdt, through the rod in a steady state is given by
View Solution" A metal rod of area of cross section A has length L and coefficient of thermal conductivity K The thermal resistance of the rod is "
View Solution
