An ant travels along a long rod with a constant velocity ii relative to the rod starting from the origin. The rod is kept initially along the positive x-axis. At t = 0, the rod also starts rotating with an angular velocity w (anticlockwise) in x-y plane about origin. Then Solution in Gujrati
the position of the ant at any time t is ¯r=ut(cosωtˆi+sinωˆtj)
the speed ofthe ant at any time t is u√1+ω2t2
the magnitude of the tangential acceleration of the ant at uny time t is ω2tu√1+ω2t2
the speed of the ant at any time t is √1+2ω2t2u
The correct Answer is:A, B, C
Step by step video & image solution for An ant travels along a long rod with a constant velocity ii relative to the rod starting from the origin. The rod is kept initially along the positive x-axis. At t = 0, the rod also starts rotating with an angular velocity w (anticlockwise) in x-y plane about origin. Then by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- CIRCULAR MOTIONBOOK - ALLEN CHAPTER - CIRCULAR MOTIONEXERCISE - Martrix match
1 Videos
- CIRCULAR MOTIONBOOK - ALLEN CHAPTER - CIRCULAR MOTIONEXERCISE - EXERCISE(O-2)
7 Videos
- CIRCULAR MOTIONBOOK - ALLEN CHAPTER - CIRCULAR MOTIONEXERCISE - EXERCISE(O-1)
22 Videos
- BASIC MATHSBOOK - ALLEN CHAPTER - BASIC MATHSEXERCISE - Question
1 Videos
- CURRENT ELECTRICITYBOOK - ALLEN CHAPTER - CURRENT ELECTRICITYEXERCISE - EX.II
66 Videos
Similar Questions
A block is placed on a horizontal table which can rotate about its axis.The block is placed at certain distance from centre as shown in figure. Table rotates such that particle does not slide. See possible direction of net acceleration of block at the instant shown in figure
Column-IColumn-II(A)When rotation is clockwise with constant ω(P)1(B)When rotation is clock wise with decreasing ω(Q)2(C)When rotation is clockwise with increasing ω(R)3(D)Just after clockwise rotation beings from rest(S)4
View SolutionA ring of radius 'r' and mass per unit length 'm' rotates with an angular velocity 'ω' in free space then the tension is :
View SolutionThe area of the parallelogram represented by the vectors →A=2ˆi+3ˆj and →B=ˆi+4ˆj is
View SolutionFind dydx for the following :
(i) y=x7/2 (ii) y=x−3
(iii)y=x (iv) y=x5+x3+4x1/2+7
(v) y=5x4+6x3/2+9x (vi) y=ax2+bx+C
(Vii)y=3x^(5)-3x-1/x
View SolutionIn the Bohr's model of hy drogen atom, the electron moves around the nucleus in a circular orbit of radius 5×10−11m. Its time period is 1.5×10−16s. The current associated with the electron motion is:-
View SolutionA uniform rod of mass m and length l rotates in a horizontal plane with an angular velocity ω about a vertical axis passing through one end. The tension in the rod at a distance x from the axis is
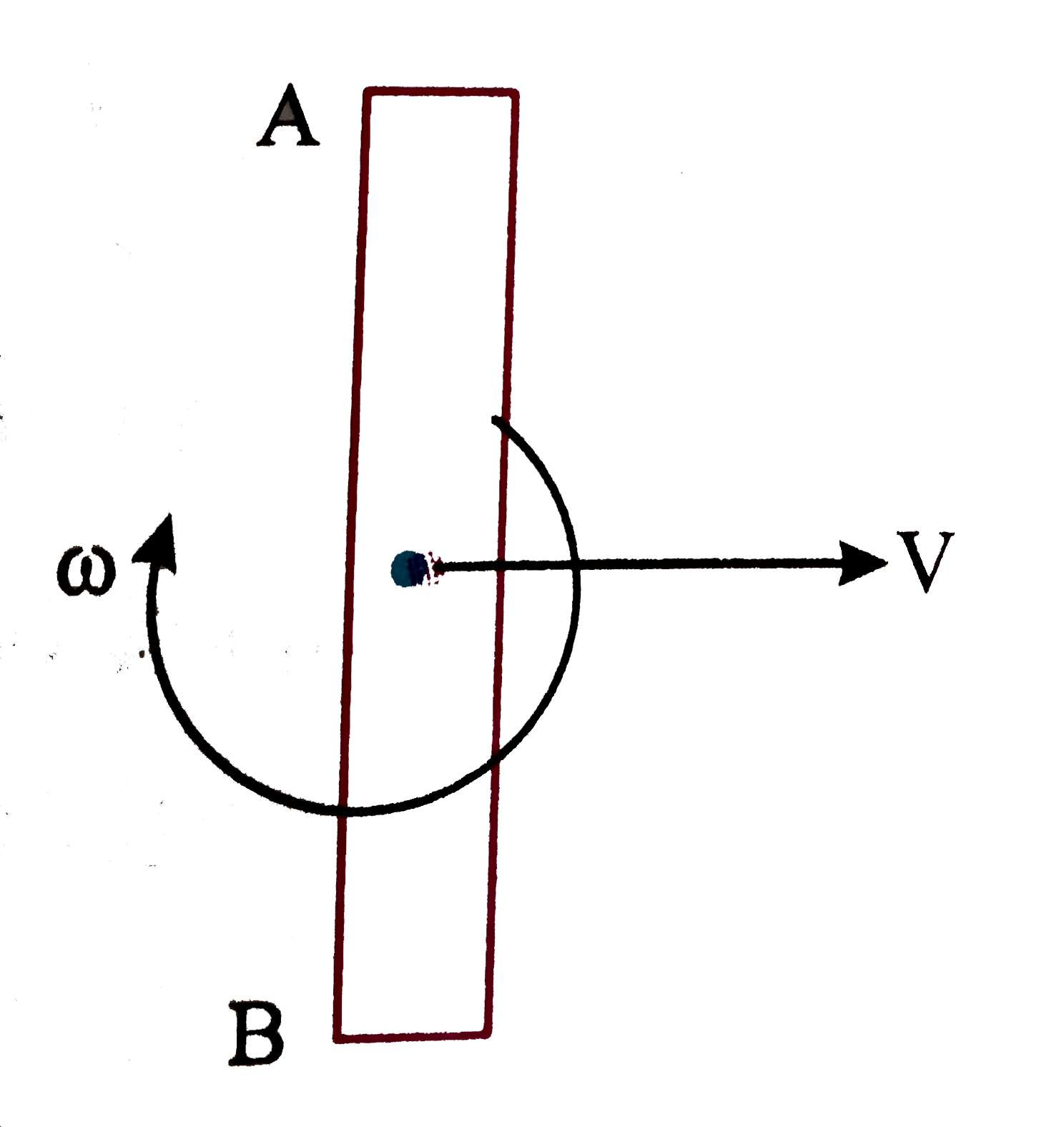
View SolutionA rod of length l is travelling with velocity v and rotating with angular velocity ω such that ωl2=v. The distance travelled by end B of the rod when rod rotates by an angle π2 is
View SolutionA rod PQ of length L revolves in a horizontal plane about the axis YY´. The angular velocity of the rod is w. If A is the area of cross-section of the rod and r be its density, its rotational kinetic energy is
View SolutionA charged rod having charge as shown is rotating with angular velocity omega about on hinge at its centre. At the instant shown rod is along x- axis Consider effect of field at the instant shown.
View SolutionA non–uniform thin rod of length L is placed along x-axis as such its one of ends at the origin. The linear mass density of rod is lambda=lambda_(0)x . The distance of centre of mass of rod from the origin is :
View SolutionA conducting rod of length L lies in X - Y plane and makes an angle 30∘ with the X - axis . One end of the rod lies at origin initially. A magnetic field also exists in the region pointing along positive Z - direction. The magnitude of the magnetic field varies with Y as B0(yL)3 where B0 is a constant. At some instant the rod starts moving with a velocity v0 along X - axis. The emf induced in the rod is
View SolutionA conducting rod of length L lies in XY-plane and makes an angle 30∘ with X-axis. One end of the rod lies at origin initially. A magnetic field also exists in the region pointing along positive Z-direction. The magnitude of the magnetic field varies with y as B0(yL)3, where,B0 is a constant. At some instant the rod stars moving with a velocity v0 along X-axis
The emf induced in the rod is
View SolutionA rod is rotating with angular velocity omega about axis AB. Find costheta .
View SolutionA smooth rod of length l rotates freely in a horizontal plane with the angular velocity about a stationary vertical axis O as shown in Fig. The moment of inertia of the rod is equal to I relative to the axis. A small ring of mass m is located on the rod close to the rotation axis and is tied to it by a thread. When the thread is burned, the ring starts sliding radially outwards along the rod. Find the velocity v of the ring relative to the rod as a function of its distance r from the rotation axis.
View SolutionA rod is rotating with angular velocity omega about axis AB. Find costheta .
View SolutionA small bead of mass M is launched from the end of a horizontal rod at a speed u along rod having same mass M. The rod is free to rotate in a vertical plane about a end. Simultaneously the rod is given a angular velocity omega as shown in the figure. Find the angular acceleration of the rod. [The rod is hinged at an end]
View Solution
