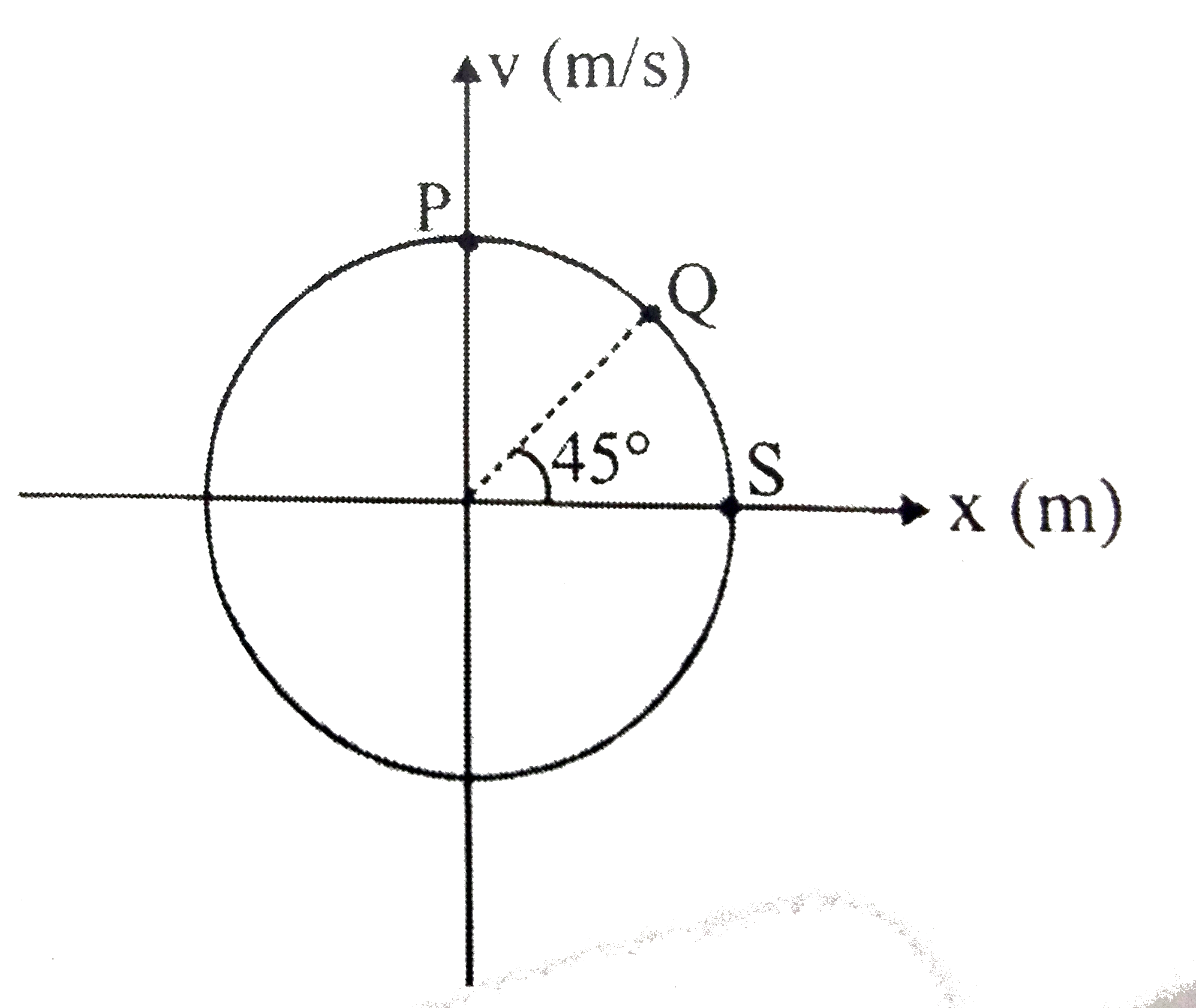
A particle is in motion on the x-axis. The variation ofits velocity with position is as shown. The graph is circle and its equation is x2+v2=1, where x is in m and v in m/s. The correct statement(s) is/are:-
 Solution in Gujrati
Solution in Gujrati
When x is positive, acceleration is negative.
When x is negative, acceleration is positive
At Q, acceleration has magnitude 1√2m/s2
At S, acceleration is infinite
The correct Answer is:A, B, C
Step by step video & image solution for A particle is in motion on the x-axis. The variation ofits velocity with position is as shown. The graph is circle and its equation is x^(2)+v^(2)=1, where x is in m and v in m/s. The correct statement(s) is/are:- by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- CIRCULAR MOTIONBOOK - ALLEN CHAPTER - CIRCULAR MOTIONEXERCISE - Martrix match
1 Videos
- CIRCULAR MOTIONBOOK - ALLEN CHAPTER - CIRCULAR MOTIONEXERCISE - EXERCISE(O-2)
7 Videos
- CIRCULAR MOTIONBOOK - ALLEN CHAPTER - CIRCULAR MOTIONEXERCISE - EXERCISE(O-1)
22 Videos
- BASIC MATHSBOOK - ALLEN CHAPTER - BASIC MATHSEXERCISE - Question
1 Videos
- CURRENT ELECTRICITYBOOK - ALLEN CHAPTER - CURRENT ELECTRICITYEXERCISE - EX.II
66 Videos
Similar Questions
A block is placed on a horizontal table which can rotate about its axis.The block is placed at certain distance from centre as shown in figure. Table rotates such that particle does not slide. See possible direction of net acceleration of block at the instant shown in figure
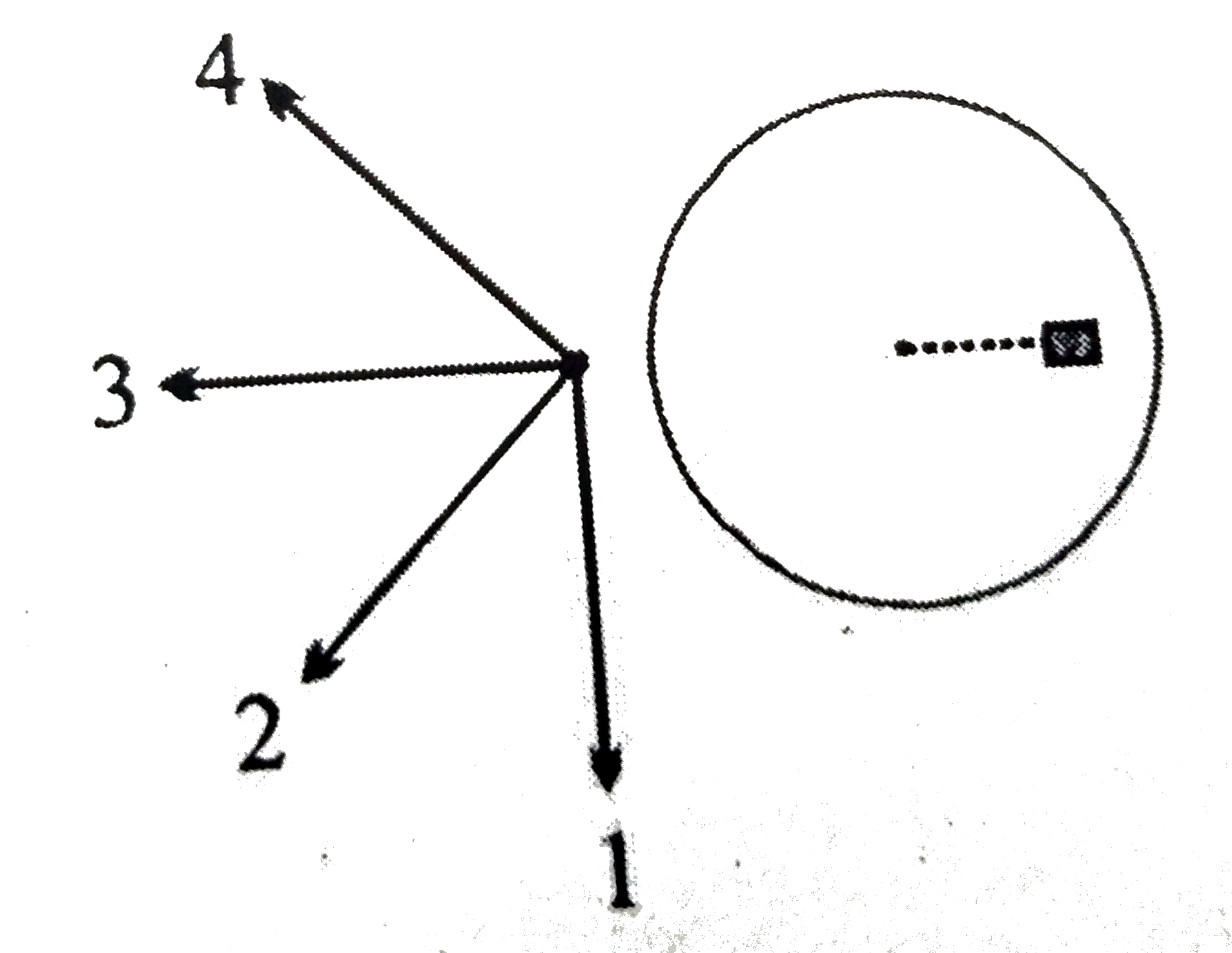
Column-IColumn-II(A)When rotation is clockwise with constant ω(P)1(B)When rotation is clock wise with decreasing ω(Q)2(C)When rotation is clockwise with increasing ω(R)3(D)Just after clockwise rotation beings from rest(S)4
View SolutionA ring of radius 'r' and mass per unit length 'm' rotates with an angular velocity 'ω' in free space then the tension is :
View SolutionThe area of the parallelogram represented by the vectors →A=2ˆi+3ˆj and →B=ˆi+4ˆj is
View SolutionFind dydx for the following :
(i) y=x7/2 (ii) y=x−3
(iii)y=x (iv) y=x5+x3+4x1/2+7
(v) y=5x4+6x3/2+9x (vi) y=ax2+bx+C
(Vii)y=3x^(5)-3x-1/x
View SolutionIn the Bohr's model of hy drogen atom, the electron moves around the nucleus in a circular orbit of radius 5×10−11m. Its time period is 1.5×10−16s. The current associated with the electron motion is:-
View SolutionA particle starts moving with constant, velocity v=ms, from position x=5m The position time graph will be
View SolutionSTATEMENT-1 : A particle is performing simple harmonic motion along X axis with amplitude A. If a graph is plotted between velocity of particle and its X coordinate then graph will be elliptical.
STATEMENT-2 : Velocity of particle in SHM as a fuction of position is given by
v=ω√A2−X2.
View SolutionThe velocity of a particle moving in the positive direction of the X-axis varies as V=K√S where K is a positive constant. Draw V−t graph.
View SolutionThe velocity of a particle moving on the x- axis is gienv by v=x^(2)+x( for xgt0) where v is in m//s and x is in m . Find its acceleration in m//s^(2) when passing through the point x=2m
View SolutionVelocity v/s Position graph of a particle performing curvilinear motion is as shown. Then select the CORRECT statement:
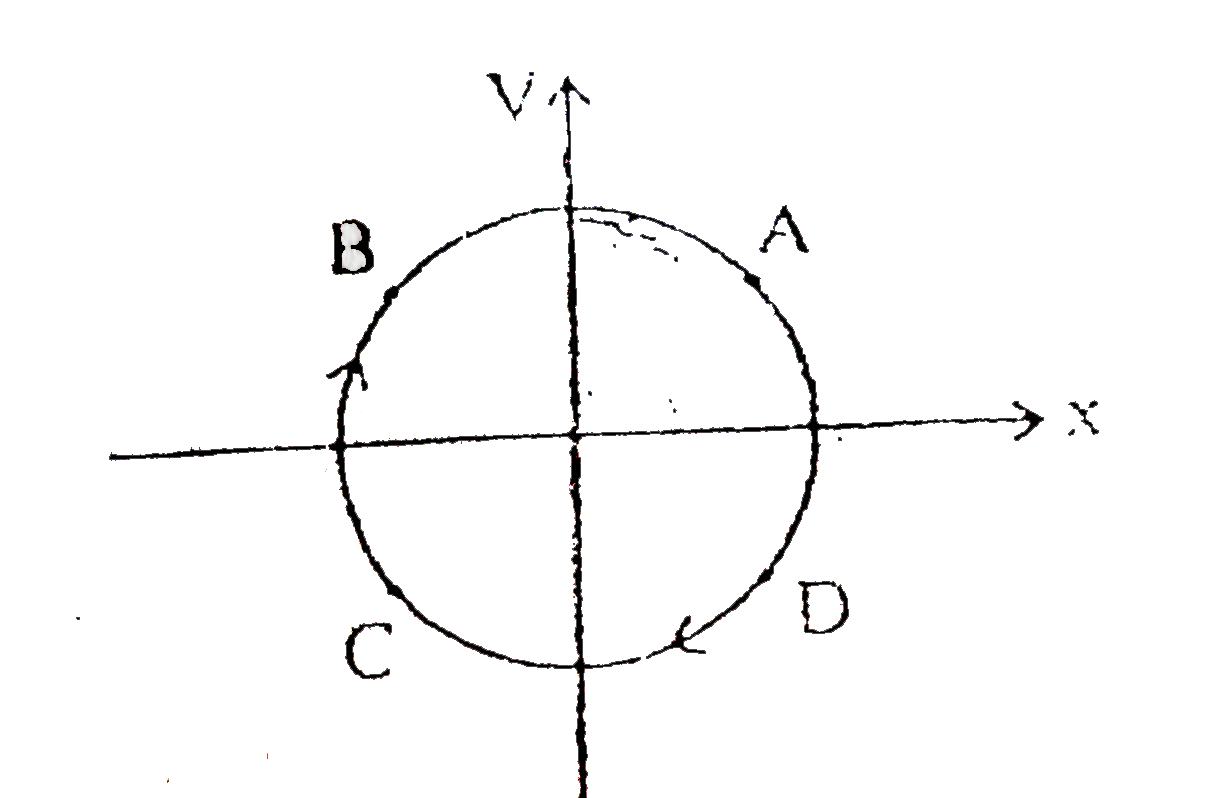
View SolutionThe velocity of a particle moving on the x-axis is given by v=x2+x, where x is in m and v in m/s. What is its position (in m) when its acceleration is 30m/s2.
View SolutionAcceleration of a particle is given by
a=1/V
Where V is the velocity . Find
(i) Velocity of particle at time t, given that v = 10 m/s at t = 0.
(ii) Velocity of particle when its position is x, given that speed is 3 m/s at x = 0.
View SolutionThe velocity of a particle moving in the positive direction of the X-axis varies as v=K√S
Where K is a positive constant.Draw V-t graph .
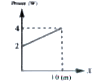
View SolutionA particle A of mass 10/7 kg is moving in the positive directio of x-axis. At initial position x=0, its velocity is 1ms−1, then its velocity (in m/s) at x=10 m is (use the graph given)
View SolutionThe velocity of a particle moving in the positive direction of the X-axis varies as V=Ksqrt(S) where K is a positive constant. Draw V-t graph.
View SolutionThe velocity of a particle moving in the positive direction of the X-axis varies as V=K√S where K is a positive constant. Draw V−t graph.
View Solution
