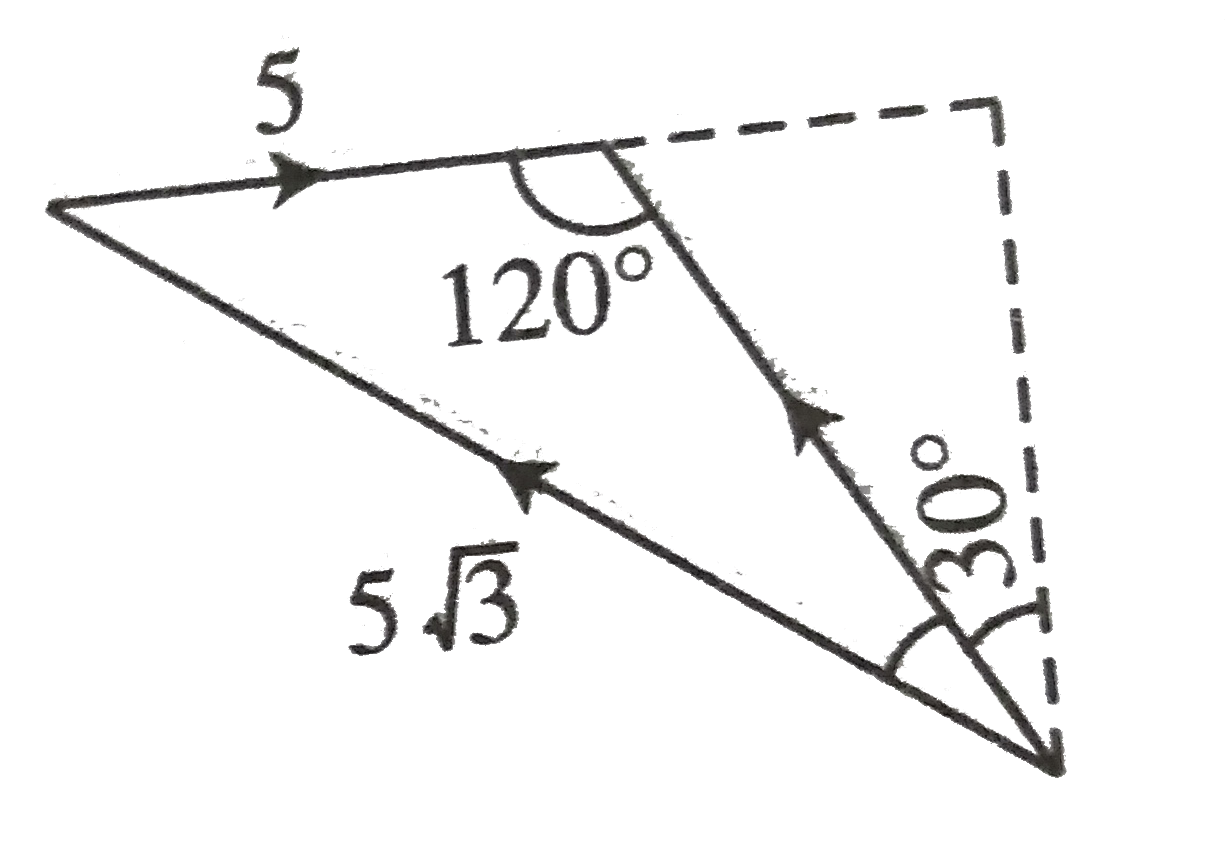
A motor boat is to reach at a point 30∘ upstream on the outer side of a river flowing with velocity 5ms−1. The velocity of motor boat with respect to water is 5(√3)ms−1. The driver should steer the boat at an angle.
 Solution in Gujrati
Solution in Gujrati
120∘ with respect to stream direction
30∘ with respect to the perpendicular to the bank
30∘ with respect to the line of destination from starting point
none of these
The correct Answer is:C
Step by step video & image solution for A motor boat is to reach at a point 30^@ upstream on the outer side of a river flowing with velocity 5 ms^(-1). The velocity of motor boat with respect to water is 5(sqrt3) ms^(-1). The driver should steer the boat at an angle. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- KINEMATICS-2DBOOK - ALLEN CHAPTER - KINEMATICS-2DEXERCISE - Exercise (O-2)
47 Videos
- KINEMATICS-2DBOOK - ALLEN CHAPTER - KINEMATICS-2DEXERCISE - Exercise (S-2)
14 Videos
- GRAVITATIONBOOK - ALLEN CHAPTER - GRAVITATIONEXERCISE - EXERCISE 4
9 Videos
- MOTION IN A PALNEBOOK - ALLEN CHAPTER - MOTION IN A PALNEEXERCISE - SOLVED EXAMPLE
28 Videos
Similar Questions
A particle is moving in xy-plane .At certain instant the components of its velocity and acceleration are as follows ux=3m/s,uy=4m/s,ax=2m/s2anday=1m/s2. The rate of change of speed at this moment is
View SolutionA particle travels so that its acceleration is given by →a=5costˆi−3sintˆj. If the particle is located at (−3,2) at time t=0 and is moving with a velocity given by (−3ˆi+2ˆj). Find
(i) The velocity [→v=∫→a.dt] at time t and
(ii) The position vector [→r=∫→v.dt] of the particle at time t(t>0).
View SolutionAssertion : The difference in the value of acceleration due to gravity at pole and equator is proportional to square of angular velocity of earth.
Reason : the value of acceleration due to gravity is minimum at the equator and maximum at the pole.
View SolutionA particle thrown over a triangle from one end of a horizontal base falls on the other end of the base after grazing the vertex. If αandβ are the base angles of triangle and angle of projection is θ, then prove that (tanθ=tanα+tanβ)
View SolutionA river is flowing towards with a velocity of 5 m s^-1 . The boat velocity is 10 ms^-1 . The boat crosses the river by shortest path. Hence,
View SolutionA motor boat is to reach at a point 30^@ upstream on the outer side of a river flowing with velocity 5 ms^(-1) . The velocity of motor boat with respect to water is 5(sqrt3) ms^(-1) . The driver should steer the boat at an angle.
View SolutionA person rows a boat in a water with a speed of 4ms−1. Water in the river is flowing with a speed of 2ms−1 . If the person rows the boat perpendiculat to thedirection of flow, find resultant velcity of the boat and time taken by boat to cross the river if widthe of the river is 400m.
View SolutionA motor boat is to reach at point 30^(@) upsteam (w.rt. Normal) on other side of a river flowing with velocity 5m//s . Velocity of motorboat w.r.t. water is 5sqrt(3) m//s . The driver should steer the baot at an angular
View SolutionA man can row a boat in still water with a velocity of 8 kmph .Water is flowing in a river with a velocity of 4 kmph . At what angle should he row the boat so as to reach the exact opposite point
View SolutionA motor boat is to reach at a point 30∘ upstream on the outer side of a river flowing with velocity 5ms−1. The velocity of motor boat with respect to water is 5(√3)ms−1. The driver should steer the boat at an angle.

View SolutionA boat crossing a river moves with a velocity v relative to still water. The river is flowing with a velocity v/2 with respect to the bank. The angle with respect to the flow direction with which the boat should move to minimize the drift is–
View SolutionVelocity of the boat with respect to river is 10m/s. From point A it is steered in the direction shown. Where will it reach on the opposite bank ?

View Solutionsqrt(3) times the velocity of a boat on still water is twice the velocity of current of a river. At what angle , with respect to the current, should the boat be steered so as to cross the river in least distance ?
View SolutionThe resistance offered by the stream of water on motor boat moving with uniform velocity of 30msec−1 is 5000 N. The power of motor boat is:
View SolutionThe velocity of a motor boat with respect to still water is 7ms^(-1) and velocity of water in a river is 3ms^(-1) . When the boat starts moving upstream a float was dropped from it . The boat travels 4.2 km and returns and reaches the float. The time taken by the goat to cath the float is
View Solutionएक नाव को धारा को प्रतिकूल दिशा में 30∘ (अभिलम्ब से) दूसरी ओर स्थित बिन्दु पर पहुचना है। नदी 5m/s के वेग से बह रही है। नाव का जल के सापेक्ष वेग 5√3m/s है। नाविक को किसी कोण पर नाव चलानी होगा।
View Solution
