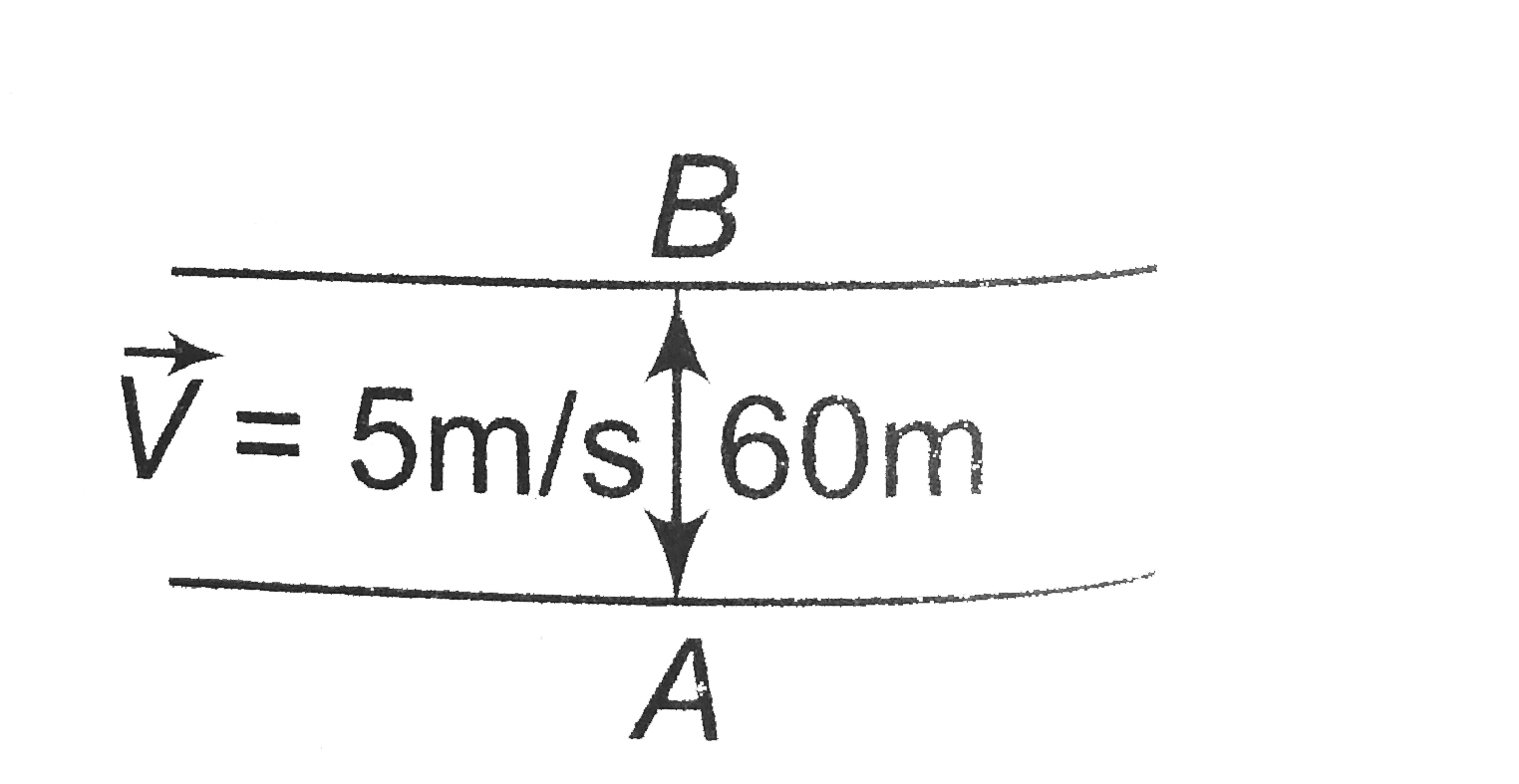
A man is crossing a river flowing with velocity of 5m/s. He reaches a point directly across at a distance of 60m in 5 sec. His velocity in still water should be
 Solution in Gujrati
Solution in Gujrati
12 m/s
13 m/s
5 m/s
10 m/s
The correct Answer is:B
Step by step video & image solution for A man is crossing a river flowing with velocity of 5m//s. He reaches a point directly across at a distance of 60m in 5 sec. His velocity in still water should be by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- KINEMATICS-2DBOOK - ALLEN CHAPTER - KINEMATICS-2DEXERCISE - Exercise (O-2)
47 Videos
- KINEMATICS-2DBOOK - ALLEN CHAPTER - KINEMATICS-2DEXERCISE - Exercise (S-2)
14 Videos
- GRAVITATIONBOOK - ALLEN CHAPTER - GRAVITATIONEXERCISE - EXERCISE 4
9 Videos
- MOTION IN A PALNEBOOK - ALLEN CHAPTER - MOTION IN A PALNEEXERCISE - SOLVED EXAMPLE
28 Videos
Similar Questions
A particle is moving in xy-plane .At certain instant the components of its velocity and acceleration are as follows ux=3m/s,uy=4m/s,ax=2m/s2anday=1m/s2. The rate of change of speed at this moment is
View SolutionA particle travels so that its acceleration is given by →a=5costˆi−3sintˆj. If the particle is located at (−3,2) at time t=0 and is moving with a velocity given by (−3ˆi+2ˆj). Find
(i) The velocity [→v=∫→a.dt] at time t and
(ii) The position vector [→r=∫→v.dt] of the particle at time t(t>0).
View SolutionAssertion : The difference in the value of acceleration due to gravity at pole and equator is proportional to square of angular velocity of earth.
Reason : the value of acceleration due to gravity is minimum at the equator and maximum at the pole.
View SolutionA particle thrown over a triangle from one end of a horizontal base falls on the other end of the base after grazing the vertex. If αandβ are the base angles of triangle and angle of projection is θ, then prove that (tanθ=tanα+tanβ)
View SolutionA man wishes to cross a river of width 120 m by a motorboat. His rowing speed in still water is 3m/s and his maximum walking speed is 1m/s. The river flows with velocity of 4m/s.
(a) Find the path which he should take to get to the point directly opposite to his starting point in the shortest time.
(b) Also, find the time which he takes to reach his destination.
View SolutionA river is flowing from east to west at a speed of 5m/min. A man on south bank of river, capable of swimming 10m/min in still water, wants to swim across the river in shortest time. He should swim
View SolutionA man can row a boat in still water with a velocity of 8 kmph .Water is flowing in a river with a velocity of 4 kmph . At what angle should he row the boat so as to reach the exact opposite point
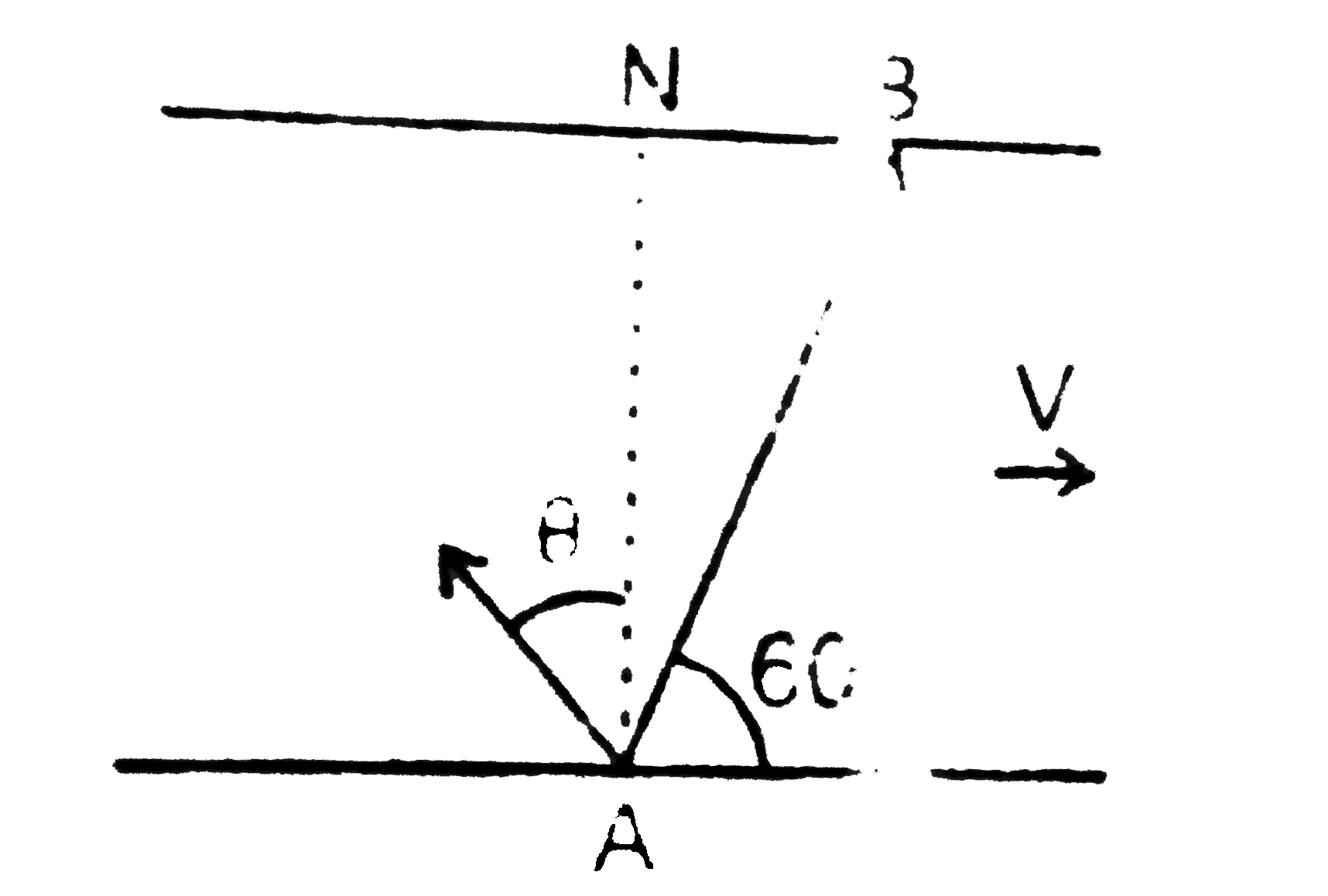
View SolutionA swimmer wands to cross a river and reach point B directly from A. The speed of the wimmer in still river and that of river flow are same. The dotted line AN is normal to flow direction of river. For swimmer to reach point B, the angle his velocity relative to river will make with line AN is given by θ. then the value of θ is :
View SolutionA swimmer starts to swim from point a to cross a river. He wants to reach point B on the opposite side of the river. The line AB makes an angle 60∘ with the river flow as hown. The velocity of the swimmer in still water is same as that of the water

(i) In what direction should he try to direct his velocity ? Calculate angle between his velocity anf river velocity.
(ii) Find the ratio of the time taken to cross the river in this situation to the minimum time in which he can cross this river.
View SolutionA man wishes to swim across a river 0.5km. wide if he can swim at the rate of 2 km/h. in still water and the river flows at the rate of 1km/h. The angle (w.r.t. the flow of the river) along which he should swin so as to reach a point exactly oppposite his starting point, should be:-
View SolutionA man can swim with a certain speed, in still water to cross a river to a point directly opposite to the starting point in time t0. When the river flows, he crosses the river directly along the same path in a time t1, If 'd' be the river width, Then the velocity of water current is:
View SolutionA river of width 80m is flowing at 6 m/s. A motorboat crosses the river in 10s and reaches a point directly across on the other river bank. The velocity of motorboat in still water is :
View SolutionA river is flowing with a velocity of 2m/s. If the width of river in 100 m and swimmer wants to cross river is shortest time, what time (in sec) would he take if velocity of swimmer in still water is 4 m/s ?
View SolutionA man can reach the point directly opposite on the other bank of a river by swimming across the river in time t_1 and crosses the same distance in time t_2 while swimming along the current. If the velocity of the man in still water is v and velocity of the water current is u , find the ratio between t_1 and t_2 .
View SolutionA man can swim with a certain spee, in still water to cross a river to a point directly opposite to the starting point in time t0. When the river flows. He crosses the river directly along the same path in a time t1. If 'd' be the river width, then the velocity of water current is
View SolutionA man wishes to cross a river of width 120 m by a motorboat. His rowing speed in still water is 3m/s and his maximum walking speed is 1m/s. The river flows with velocity of 4m/s.
(a) Find the path which he should take to get to the point directly opposite to his starting point in the shortest time.
(b) Also, find the time which he takes to reach his destination.
View Solution
