The height (in meters) at any time t (in seconds) of a ball thrown vertically varies according to equation h(t)=−16t2+256t. How long after in seconds the ball reaches the hightest point Solution in Gujrati
The correct Answer is:8sec
Step by step video & image solution for The height (in meters) at any time t (in seconds) of a ball thrown vertically varies according to equation h(t)=-16t^(2)+256t. How long after in seconds the ball reaches the hightest point by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- RACEBOOK - ALLEN CHAPTER - RACEEXERCISE - Basic Maths (Integration)
12 Videos
- RACEBOOK - ALLEN CHAPTER - RACEEXERCISE - Basic Maths (Graphs))
28 Videos
- RACEBOOK - ALLEN CHAPTER - RACEEXERCISE - Basic Maths (Trigonometry)
22 Videos
- NEWTONS LAWS OF MOTIONBOOK - ALLEN CHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - EXERCISE-III
28 Videos
- SIMPLE HARMONIC MOTIONBOOK - ALLEN CHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Example
1 Videos
Similar Questions
Find the value of x1, so that ∫x10ydx=5
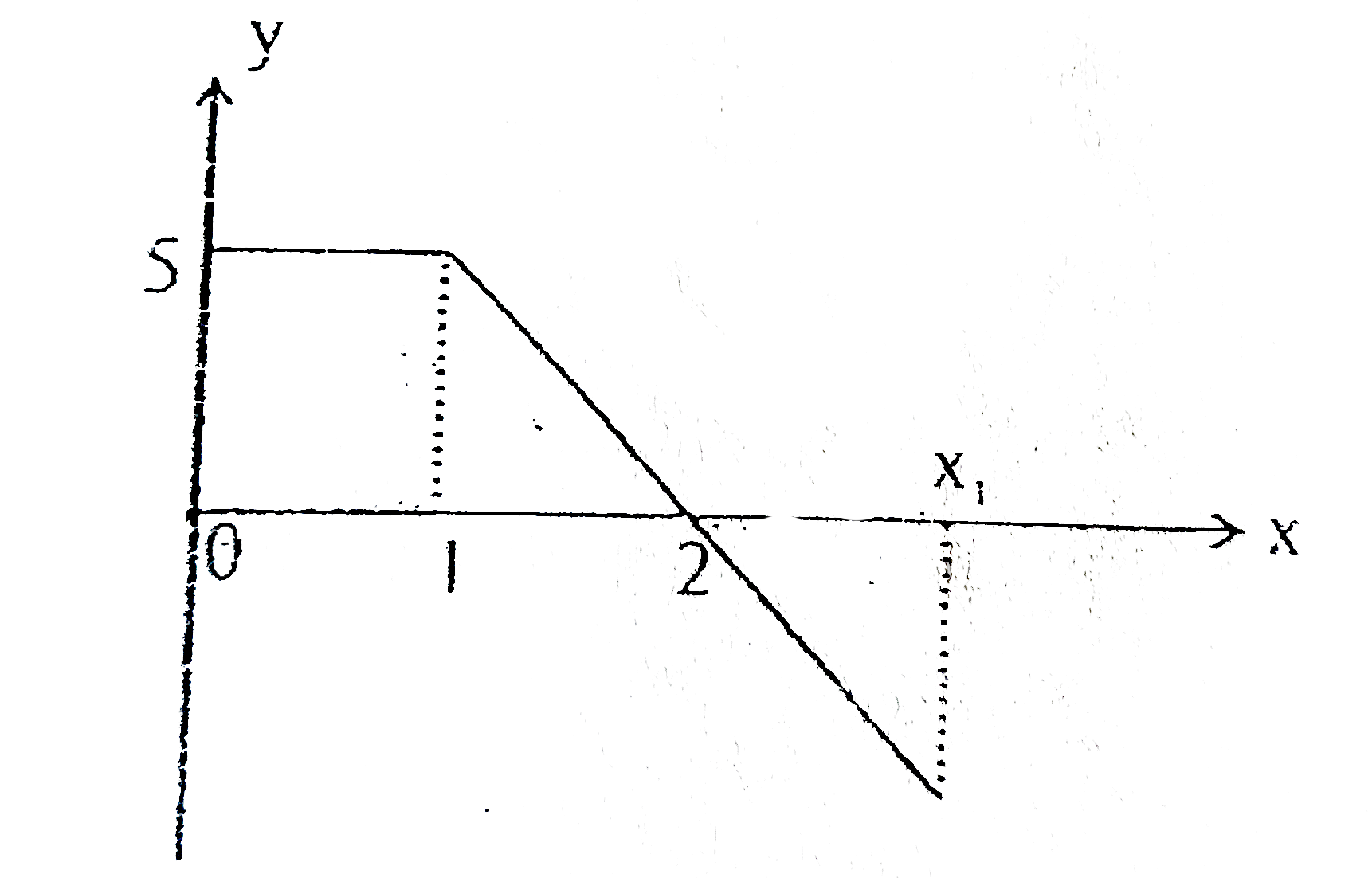
View SolutionWhich of the following equation is best representation of following graph's?
View SolutionConvert the angle from degree to radian :
(a) 30∘(b) 45∘(c) 60∘(d) 90∘(e) 120∘(f) 135∘(g) 210∘(h) 270∘(i) 315∘
View SolutionAssertion: The driver in a vechicle moving with a constant speed on a straight road is in a non-inertial frame of referance.
Reason: A reference frame in which Newton's laws of motion are applicable is non-inertial.
View SolutionA rod with rectangular cross section oscillates about a horizontal axis passing through one of its ends and it behaves like a seconds pendulum, its length will be
View SolutionThe height of a ball thrown into the air with an initial vertical velocity of 24 fts from a height of 6 feet above the ground is given by the equation: h=16t^(2)+24t+6, where t is the time in seconds,for the ball has been in air. After how many seconds is the ball at a height of 14 feets
View SolutionThe height (in meters) at any time t (in seconds) of a ball thrown vertically varies according to equation h(t)=−16t2+256t. How long after in seconds the ball reaches the hightest point
View SolutionA stone thrown vertically upward satisfies the equation s=64t−16t2 where is in meter and t is second .What is the time required to reach the maximum height ?
View Solutionएक गेंद h मीटर ऊंची मीनार की चोटी से विरामावस्था से छोड़ दी जाती है । यह T सेकण्ड बाद पृथ्वी पर पहुंचती है। T/3 सेकण्ड पर गेंद की स्थिति क्या है?
View Solutionh(t)=144t−16t2
The function above represents the height, in feet, a ball reaches t seconds after it is tossed in the air from groud level.
a. What is the maximum height of the ball?
b. After how many seconds will the ball hit the ground before rebounding?
View SolutionWhen a ball is thrown straight up at an initial velocity of 54 feet per second. The height of the ball t seconds after it is thrown is given by the function h(t)=54t−12t2. How many seconds after the ball is thrown will it return to the ground?
View Solutionएक गेंद ऊर्ध्वाधर ऊपर फेंकी जाने पर t समय में अधिकतम ऊँचाई h पर पहुँचती है t/2 समय उपरान्त उसकी ऊँचाई होगी :
View SolutionA stone is thrown up vertically. The height it reaches at time t seconds is given by x=80t−16t2. The stone reaches the maximum height in time t seconds is given by
View Solutionh=−4.9t2+25t
The equation above expresses the approximate height h, in meters, of a ball t seconds after it is launched vertically upward from the ground with an initial velocity of 25 meters per second. After approximately how many seconds will the ball hit the ground?
View SolutionThe height h , in feet , of a ball shot upward from a ground level spring gun is described by the formula h=−16t2+48t. Where t is the time in seconds. What is the maximum height , in feet , reached by the ball ?
View SolutionJoe throws a ball upwards from a height of 12 feet from ground level. The height of the ball above the ground after time t second from when the ball was thrown is given by the expression h(t)= −t2+at+b . The ball comes back to the ground after 8 second. What is the value of (a+b)?
View Solution
