Position of particle moving along x-axis is given as x=2+5t+7t2 then calculate :Solution in Gujrati
Velocity (i.edxdt) of particle
Initial velocity(i.edxdt att=0)
Velocity at t=2sec
Accleration(i.ed2xdt2) of particle
The correct Answer is:A, B, C, D
Step by step video & image solution for Position of particle moving along x-axis is given as x=2+5t+7t^(2) then calculate : by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- RACEBOOK - ALLEN CHAPTER - RACEEXERCISE - Basic Maths (Integration)
12 Videos
- RACEBOOK - ALLEN CHAPTER - RACEEXERCISE - Basic Maths (Graphs))
28 Videos
- RACEBOOK - ALLEN CHAPTER - RACEEXERCISE - Basic Maths (Trigonometry)
22 Videos
- NEWTONS LAWS OF MOTIONBOOK - ALLEN CHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - EXERCISE-III
28 Videos
- SIMPLE HARMONIC MOTIONBOOK - ALLEN CHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Example
1 Videos
Similar Questions
Find the value of x1, so that ∫x10ydx=5
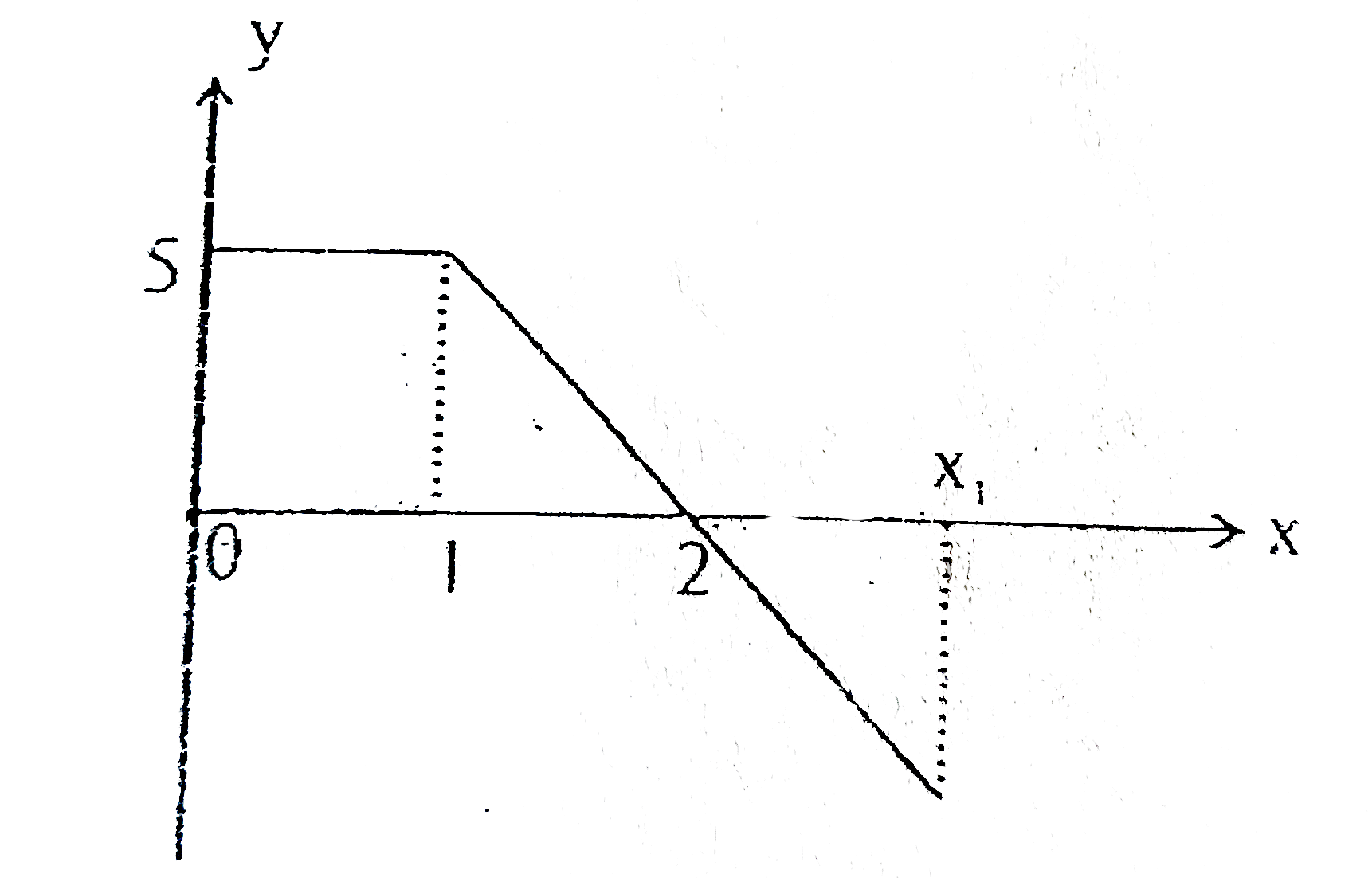
View SolutionWhich of the following equation is best representation of following graph's?
View SolutionConvert the angle from degree to radian :
(a) 30∘(b) 45∘(c) 60∘(d) 90∘(e) 120∘(f) 135∘(g) 210∘(h) 270∘(i) 315∘
View SolutionAssertion: The driver in a vechicle moving with a constant speed on a straight road is in a non-inertial frame of referance.
Reason: A reference frame in which Newton's laws of motion are applicable is non-inertial.
View SolutionA rod with rectangular cross section oscillates about a horizontal axis passing through one of its ends and it behaves like a seconds pendulum, its length will be
View SolutionA particle moves along x-axis such that its position veries with time as x=50t-5t^2 . Select the correct alternative (s).
View SolutionPosition of a particle moving along x-axis is given by x=2+8t-4t^(2) . The distance travelled by the particle from t=0 to t=2 is:-
View SolutionIf the velocity of a particle moving along x-axis is given as v=(3t2−2t) and t=0, x=0 then calculate position of the particle at t=2sec.
View SolutionThe position of a particle moving along x- axis is given by x=x_0 cos^2(omegat) . Its when it is at mean position is
View SolutionThe displacement (in metre) of a particle moving along x-axis is given by x=18t+5t^2.Calculate (i) the instantaneous velocity at t=2s.
View SolutionThe position of a particle moving along a straight line is given by x =2 - 5t + t ^(3). Find the acceleration of the particle at t =2 s. (x is metere).
View SolutionThe position of a particle moving along a. straight line is given by x=2−5t+t3 The acceleration of the particle at t = 2 sec. is ...... Here x is in meter.
View SolutionThe displacement (in metre) of a particle moving along x-axis is given by x=18t +5t^(2) Calculate (i) instantaneous acceleration.
View SolutionA particle moves along x-axis such that its position veries with time as x=50t−5t2. Select the correct alternative (s).
View SolutionThe displacement (in meter)of a particle, moving along x-axis is given by x=18t + 5t^2 . Calculate instantaneous velocity at t = 2s
View SolutionThe displacement (in meter)of a particle, moving along x-axis is given by x=18t+5t2 . Calculate
instantaneous acceleration.
View Solution
