If the velocity of a particle moving along x-axis is given as v=(3t2−2t) and t=0, x=0 then calculate position of the particle at t=2sec. Solution in Gujrati
The correct Answer is:x=4
(Hint :- change in position Δx=∫vdt)
Topper's Solved these Questions
- RACEBOOK - ALLEN CHAPTER - RACEEXERCISE - Basic Maths (Graphs))
28 Videos
- RACEBOOK - ALLEN CHAPTER - RACEEXERCISE - Basic Maths (Co-ordinate & Algebra)
40 Videos
- RACEBOOK - ALLEN CHAPTER - RACEEXERCISE - Basic Maths (Differentiation)
40 Videos
- NEWTONS LAWS OF MOTIONBOOK - ALLEN CHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - EXERCISE-III
28 Videos
- SIMPLE HARMONIC MOTIONBOOK - ALLEN CHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Example
1 Videos
Similar Questions
Which of the following equation is best representation of following graph's?
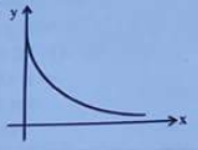
View SolutionFind the value of :-
(i)√4
(ii)√9
(iii)√16
(iv)sqrt(36)
View SolutionFor a straight line y=43x−4. Choose correct alternate(s)
View SolutionAssertion: The driver in a vechicle moving with a constant speed on a straight road is in a non-inertial frame of referance.
Reason: A reference frame in which Newton's laws of motion are applicable is non-inertial.
View SolutionA rod with rectangular cross section oscillates about a horizontal axis passing through one of its ends and it behaves like a seconds pendulum, its length will be
View SolutionThe velocity of a particle moving in the positive direction of x-axis veries as v=10√x. Assuming that at t=0, particle was at x=0
View SolutionThe velocity of a particle moving in the positive direction of X-axis varies as v=5sqrt(x) . Assuming that at t = 0, particle was at x = 0. What is the acceleration of the particle ?
View SolutionPosition of a particle moving along x-axis is given by x=2+8t-4t^(2) . The distance travelled by the particle from t=0 to t=2 is:-
View SolutionThe position (x) of a particle of mass 2 kg moving along x-axis at time t is given by x=(2t3) metre. Find the work done by force acting on it in time interval t=0 to t=2 is :-
View SolutionPosition of a particle moving along a straight line is given by x=2t^(2)+t . Find the velocity at t = 2 sec.
View SolutionThe displacement of particle moving along x-axis is given by x=6t+12t^(2) , calculate the instantaneous velocity at t=0 and t=2s.
View SolutionThe position of the particle moving along x-axis is given by x=2t-3t^(2)+t^(3) where x is in mt and t is in second.The velocity of the particle at t=2sec is
View SolutionThe acceleration of a particle is given by a = 3t and at t = 0, v = 0, x = 0. The velocity and displacement at t = 2 sec will be-
View Solutionएक कण चाल v=b√x से धनात्मक X-अक्ष की दिशा में चल रहा है। समय t=τ पर कण की चाल होगी (माना कि t=0 पर कण मूलबिंदु पर है)
View Solutionकिसी कण कि किसी क्षण t पर x - अक्ष के अनुदिश स्थिति निम्न सम्बन्ध से दी जाती है x=2+t−3t2,t=0 से t = 1 तक के समयान्तराल में कण द्वारा तय किया गया विस्थापन व दूरी होगी
View Solutionकिसी कण का त्वरण a=3t2+2t+2m/s2 द्वारा दिया जाता है, यहाँ t समय है। यदि कण t=0 पर v= 2 मी/सै से चलना प्रारम्भ करता है, तब 2 सैकण्ड पश्चात् कण का वेग होगा
View Solution
