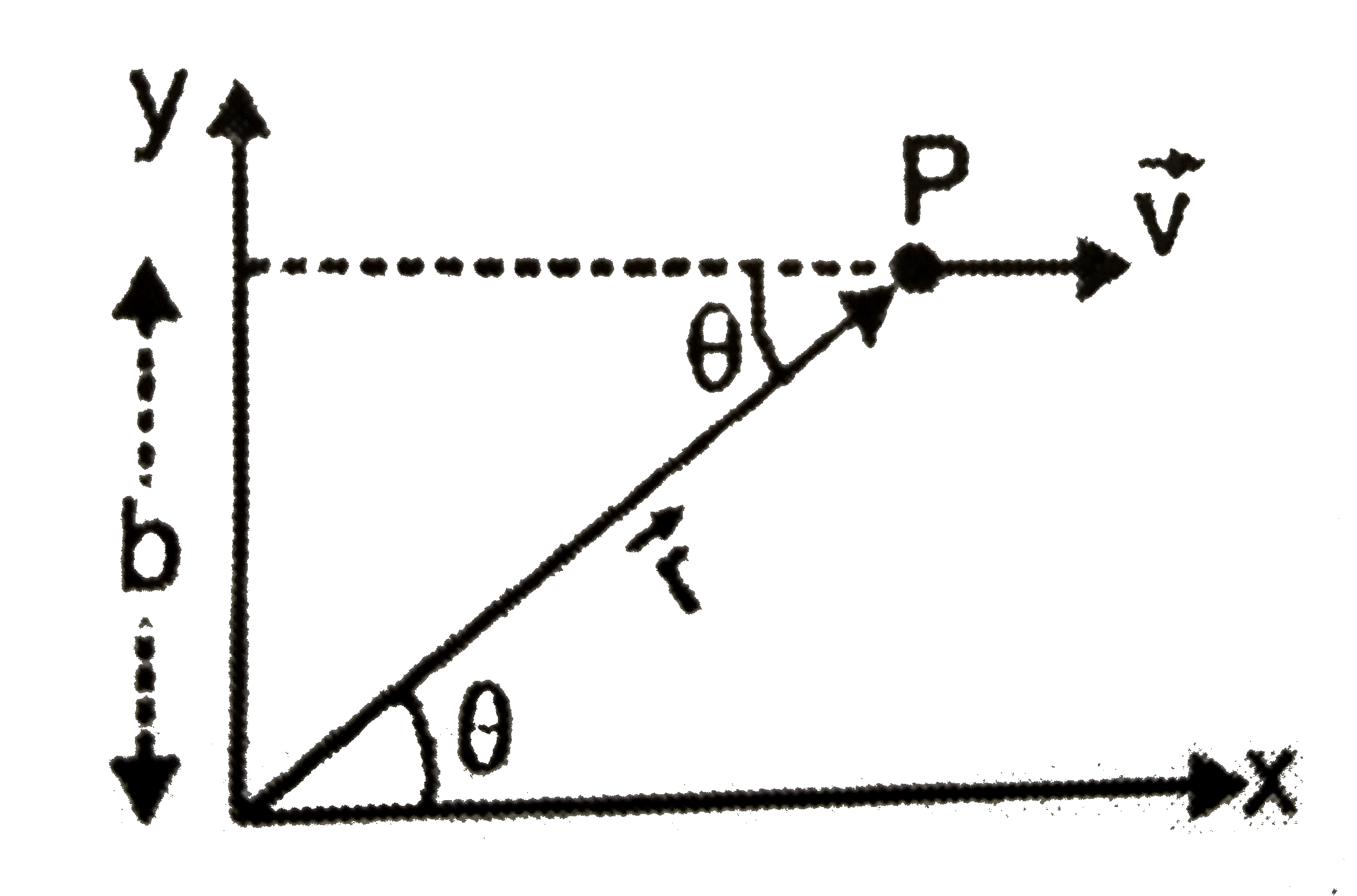
A particle is moving with constant speed v along the line y = a in positive x -direction. Find magnitude of its angular velocity about orgine when its position makes an angle θ with x-axis.Solution in Gujrati
vsin2θa
vcos2θa
vsinθ
None
The correct Answer is:A
Step by step video & image solution for A particle is moving with constant speed v along the line y = a in positive x -direction. Find magnitude of its angular velocity about orgine when its position makes an angle theta with x-axis. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- RACEBOOK - ALLEN CHAPTER - RACEEXERCISE - Basic Maths (GRAVITATION)
25 Videos
- RACEBOOK - ALLEN CHAPTER - RACEEXERCISE - Basic Maths (Properties of Matter & Fluid Mechanics)(Elasticity)
20 Videos
- RACEBOOK - ALLEN CHAPTER - RACEEXERCISE - Basic Maths (COLLISION AND CENTRE OF MASS )
12 Videos
- NEWTONS LAWS OF MOTIONBOOK - ALLEN CHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - EXERCISE-III
28 Videos
- SIMPLE HARMONIC MOTIONBOOK - ALLEN CHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Example
1 Videos
Similar Questions
Two paricles of equal mass m go round a circle of radius R under the action of their mutual gravitional attraction. The speed of each particle is
View SolutionA cable that can support a load W is cut into two equal parts .T he maximum load that can be supported by either part is
View SolutionA disc of radius r is cut from a larger disc of radius 4r in such a way that the edge of the hole touches the edge of the disc. The centre of mass of the residual disc will be a distance from centre of larger disc :-
View SolutionAssertion: The driver in a vechicle moving with a constant speed on a straight road is in a non-inertial frame of referance.
Reason: A reference frame in which Newton's laws of motion are applicable is non-inertial.
View SolutionA rod with rectangular cross section oscillates about a horizontal axis passing through one of its ends and it behaves like a seconds pendulum, its length will be
View SolutionA particle moving parallel to x-axis as shown in fig. such that at all instant the y-axis component of its position vector is constant and is equal to 'b'. Find the angular velocity of the particle about the origin when its radius vector makes angle theta from the axis.
View SolutionA particle is moving with constant speed v along the line y = a in positive x -direction. Find magnitude of its angular velocity about orgine when its position makes an angle theta with x-axis.
View SolutionA particle of mass m is moving with constant speed v on the line y=b in positive x-direction. Find its angular momentum about origin, when position coordinates of the particle are (a, b).
View SolutionA particle is moving with a contant velocity along a line parallel to positive X-axis. The magnitude of its angular momentum with respect of the origin is
View SolutionA particle is moving with constant speed v along x - axis in positive direction. Find the angular velocity of the particle about the point (0, b), when position of the particle is (a, 0).
View SolutionA particle is moving with a contant velocity along a line parallel to positive X-axis. The magnitude of its angular momentum with respect of the origin is
View SolutionA particle is moving with a contant velocity along a line parallel to positive X-axis. The magnitude of its angular momentum with respect of the origin is
View SolutionA particle is moving with a contant velocity along a line parallel to positive X-axis. The magnitude of its angular momentum with respect of the origin is
View SolutionA positively charged particle moving along x-axis with a certain velocity enters a uniform electric field directed along positive y-axis. Its
View SolutionA particle is moving along a straight line parallel to x-axis with constant velocity. Its angular momentum about the origin
View SolutionA particle moving parallel to x-axis as shown in fig. such that at all instant the y-axis component of its position vector is constant and is equal to 'b'. Find the angular velocity of the particle about the origin when its radius vector makes angle θ from the axis.
View Solution
