The number of nonzero integral values of a for which the function f(x)=x4+ax3+3x22+1 is concave upward along the entire real line is___________Solution in Bengali
Step by step video & image solution for The number of nonzero integral values of a for which the function f(x)=x^4+a x^3+(3x^2)/2+1 is concave upward along the entire real line is___________ by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Given two points A and B. If area of triangle ABC is constant then locus of point C in space is
View SolutionFind the area of the figure enclosed by the curve 5x2+6xy+2y2+7x+6y+6=0.
View SolutionThe number of nonzero integral values of a for which the function f(x)=x4+ax3+3x22+1 is concave upward along the entire real line is___________
View SolutionThe interval in which the function y=f(x)=(x-1)/(x^(2)-3x+3) transforms the real line is
View SolutionConcavity and convexity :
if f''(x)>0∀x∈(a,b) then the curve y=f(x) is concave up ( or convex down) in (a,b) and iff''(x)<0∀x∈(a,b) then the curve y=f(x) is concave down (or convex up ) in (a,b)
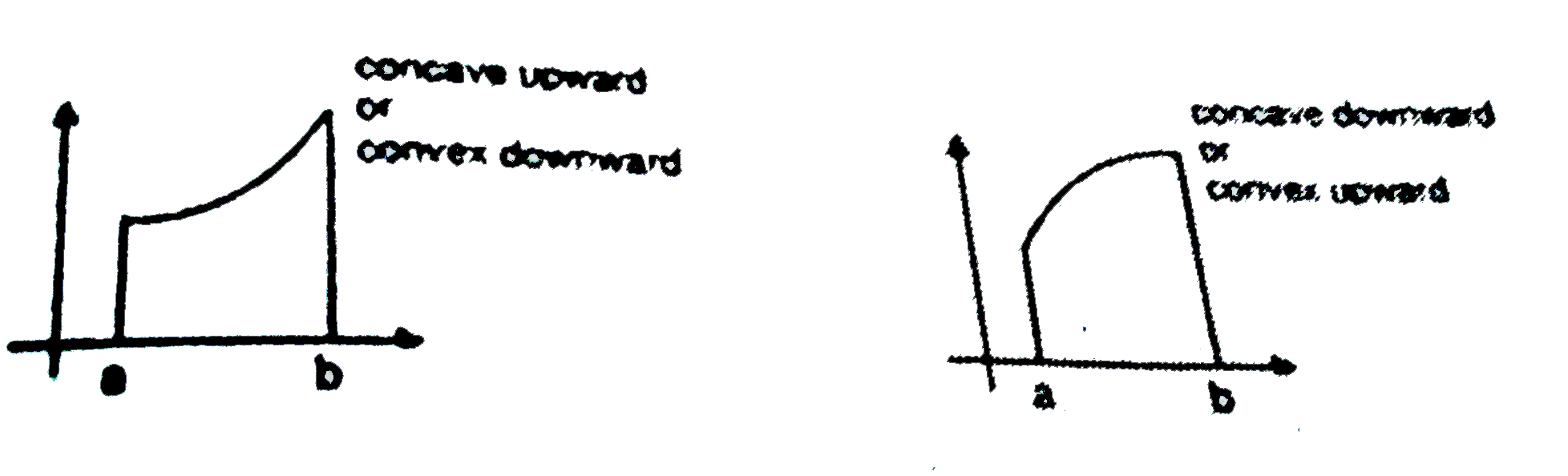
Inflection point :
The point where concavity of the curve changes is known as point of inflection (at inflection point f''(x) is equal to 0 or undefined)

Exhaustive set of values of 'a' for which the function f(x)=x4+ax3+3x22+1 will be concave upward along the entire real line is :
View SolutionIf graph of the function f(x) =3x4+2x3+ax2−x+2 is concave upward for all real x, then find values of a,
View SolutionStatement I :If f(x) is increasing function with upward concavity, then concavity of f−1(x) is also upwards.
Statement II : If f(x) is decreasing function with upwards concavity, then concavity of f−1(x) is alo upwards.
View SolutionThe function f(x)=2ax3+3x2+6(a−1)x+1 is decreasing for all real values of x .Then the greatest integral value of a is
View SolutionThe function f(x)=2ax3+3x2+6(a−1)x+1 is decreasing for all real values of x .Then the greatest integral value of a is
View SolutionThe number of nonzero integral values of a for which the function f(x)=x4+ax3+3x22+1 is concave upward along the entire real line is___________
View SolutionIf graph of the function f(x) =3x4+2x3+ax2−x+2 is concave upward for all real x, then find values of a,
View SolutionThe number of nonzero integral values of a for which the function f(x)=x4+ax3+3x22+1 is concave upward along the entire real line is___________
View SolutionStatement I :If f(x) is increasing function with upward concavity, then concavity of f−1(x) is also upwards.
Statement II : If f(x) is decreasing function with upwards concavity, then concavity of f−1(x) is alo upwards.
View SolutionConcavity and convexity :
if f''(x)>0∀x∈(a,b) then the curve y=f(x) is concave up ( or convex down) in (a,b) and iff''(x)<0∀x∈(a,b) then the curve y=f(x) is concave down (or convex up ) in (a,b)
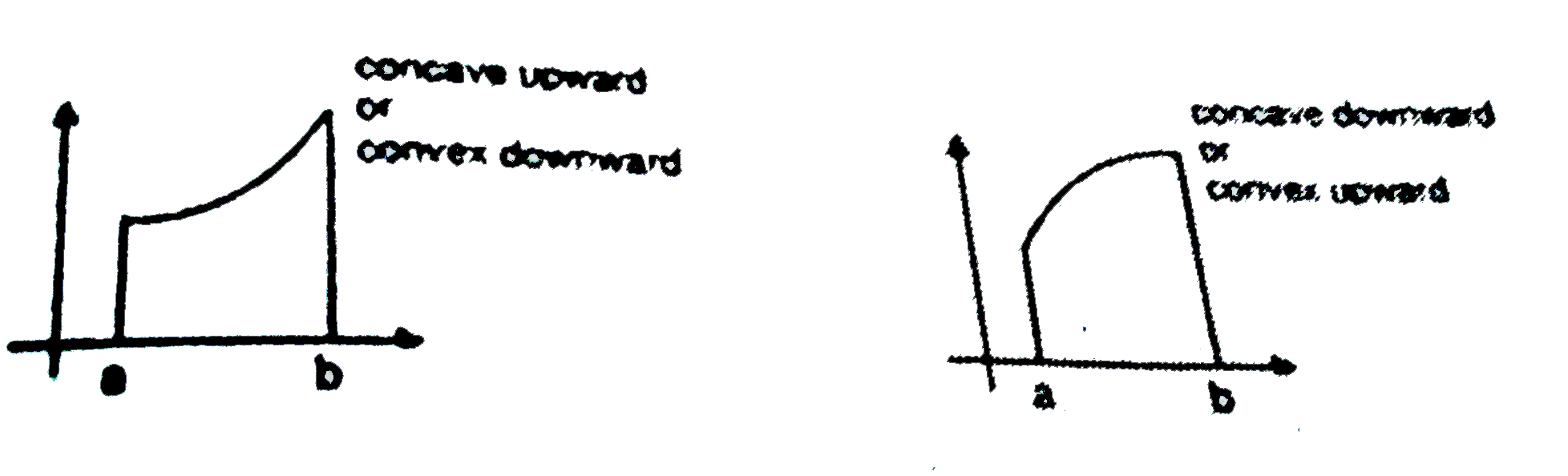
Inflection point :
The point where concavity of the curve changes is known as point of inflection (at inflection point f''(x) is equal to 0 or undefined)

Exhaustive set of values of 'a' for which the function f(x)=x4+ax3+3x22+1 will be concave upward along the entire real line is : (A) [−1,1] (B) [−2,2] (C) [0,2] (D) [0,4]
View SolutionThe interval in which the function y=f(x)=x−1x2−3x+3 transforms the real line is
View SolutionThe interval in which the function y=f(x)=x−1x2−3x+3 transforms the real line is
View Solution
