An ellipse is inscribed in a circle and a point within the circle is chosen at random. If the probability that this point lies outside the ellipse is then the eccentricity of the ellipse is: (A) (B) (C) (D) Solution in Punjabi
The correct Answer is:A
Step by step video & image solution for An ellipse is inscribed in a circle and a point within the circle is chosen at random. If the probability that this point lies outside the ellipse is 2/3 then the eccentricity of the ellipse is: (A) (2sqrt2)/3 (B) sqrt5/3 (C) 8/9 (D) 2/3 by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - ARIHANT MATHSCHAPTER - ELLIPSEEXERCISE - Exercise (More Than One Correct Option Type Questions)15videos
ELLIPSE
- BOOK - ARIHANT MATHSCHAPTER - ELLIPSEEXERCISE - Exercise (Passage Based Questions)15videos
ELLIPSE
- BOOK - ARIHANT MATHSCHAPTER - ELLIPSEEXERCISE - Exercise For Session 314videos
ELLIPSE
- BOOK - ARIHANT MATHSCHAPTER - DY / DX AS A RATE MEASURER AND TANGENTS, NORMALS EXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)7videos
DY / DX AS A RATE MEASURER AND TANGENTS, NORMALS
- BOOK - ARIHANT MATHSCHAPTER - ESSENTIAL MATHEMATICAL TOOLS EXERCISE - Exercise (Single Integer Answer Type Questions)3videos
ESSENTIAL MATHEMATICAL TOOLS
Similar Questions
The locus of extremities of the latus rectum of the family of ellipse b2x2+a2y2=a2b2 is
05:28View SolutionA conic is represented by C≡9x2+4xy+6y2−22x−16y+9=0 Q. The centre of conic C is
05:12View SolutionFind the angle between the pair of tangents from the point (1,2) to the ellipse 3x2+2y2=5.
View SolutionThe slope of the tangent to the curve (y−x5)2=x(1+x2)2 at the point (1,3) is.
05:30View SolutionThe number of solutions of the equation |x−1|−|2x−5|=2x
View SolutionThe ratio of the area of triangle inscribed in ellipse x2a2+y2b2=1 to that of triangle formed by the corresponding points on the auxiliary circle is 0.5. Then, find the eccentricity of the ellipse. (A) 12 (B) √32 (C) 1√2 (D) 1√3
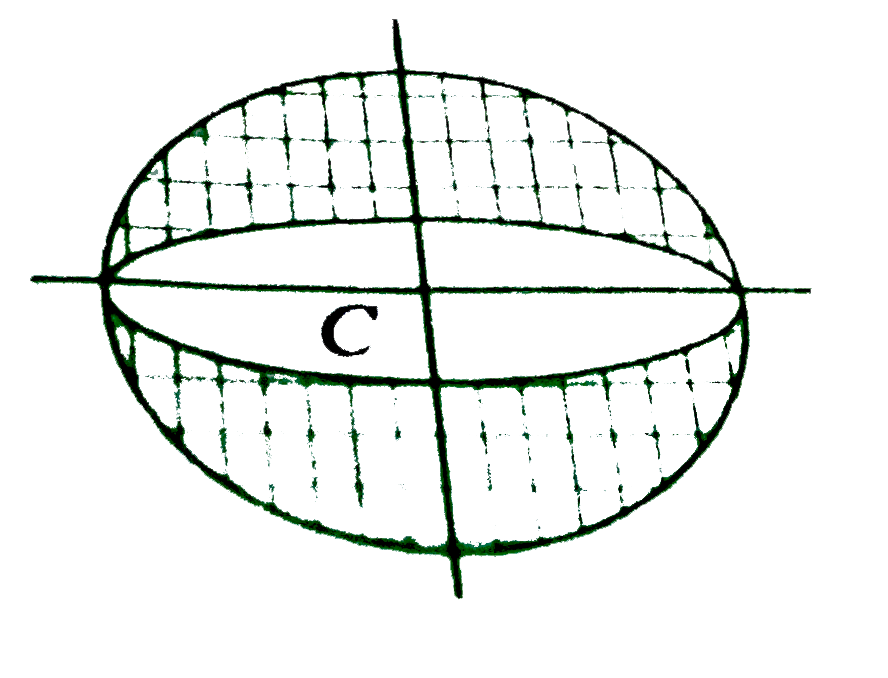
02:28View SolutionThere are some experiment in which the outcomes cannot be identified discretely. For example, an ellipse of eccentricity 2√2/3 is inscribed in a circle and a point within the circle is chosen at random. Now, we want to find the probability that this point lies outside the ellipse. Then, the point must lie in the shaded region shown in Figure. Let the radius of the circle be a and length of minor axis of the ellipse be 2b. Given that
1−b2a2=89orb2a2=19
Then, the area of circle serves as sample space and area of the shaded region represents the area for favorable cases. Then, required probability is
p=Area of shaded regionArea of circle
=πa2−πabπa2=1−ba=1−13=23
Now, answer the following questions.
A point is selected at random inside a circle. The probability that the point is closer to the center of the circle than to its circumference is02:50View SolutionAn ellipse of eccentricity 2√23 is inscribed in a circle . A point is chosen inside the cirlce at random. The probaboility that the point lies outside the ellipse is
03:47View SolutionA circle of maximum area is inscribed in an ellipse. If p is the probability that a point within the ellipse chosen at random lies outside the circle, then the eccentricity of the ellipse is
03:08View SolutionAn ellipse of eccentricity 2√23 is inscribed in a circle and a point within the circle is chosen at random. Let the probability that this point lies outside the ellipse be p. Then the value of 105 p is
05:12View SolutionThe ratio of ordinates of a point on ellipse and its corresponding point on auxiliary circle is 2√23 then its eccentricity is
01:50View SolutionIf the ratio of the ordinate of a point on ellipse and its corresponding point on auxiliary circle is 2√23 then its eccentricity is
03:26View SolutionAn ellipse is inscribed in its auxiliary circle and a point within the circle is chosen at random. If p is the probability that this point lies outside the ellipse and inside the auxiliary circle. Then 8p is equal to (where eccentricity of the ellipse is √32)
(A) 3 (B) 4 (C) 6 (D) 106:53View SolutionAn ellipse is inscribed in its auxiliary circle and a point within the circle is chosen at random. If p is the probability that this point lies outside the ellipse and inside the auxiliary circle. Then 8p is equal to (where eccentricity of the ellipse is √32)
(A) 3 (B) 4 (C) 6 (D) 105:55View SolutionAn eppipse of eccentricity 2√23 is inscribed in a circle and a point within the circle is chosen at random. The probability that this point lies outside the ellipse is
04:44View SolutionAn ellipse of eccentricity 2√23 is inscribed in a circle and a point within the circle is chosen at random. The probability that this point lies outside the ellipse is
03:11View Solution

