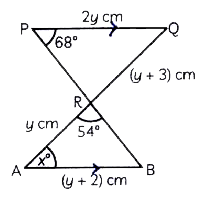
ABC is a triangle in which ∠ABC=90∘,BD is perpendicular to AC. Which of the following is TRUE?
I. Triangle BAD is similar to triangle CBD.
II. Triangle BAD is similar to triangle CAB.
III. Triangle BAD is similar to triangle CAB.
Only I
Only II and III
Only I and III
All I, II and III
To solve the problem, we need to analyze the triangles formed in triangle ABC, where angle ABC = 90 degrees and BD is perpendicular to AC. We will check the similarity of the triangles BAD, CBD, and CAB.
1. Identify the Angles in Triangle ABC:
- Given that angle ABC = 90°, we denote angle A as α and angle C as θ.
- Therefore, the angles in triangle ABC are:
- Angle A = α
- Angle B = 90°
- Angle C = θ
- Since the sum of angles in a triangle is 180°, we have:
α+90°+θ=180°
This implies:
α+θ=90°
2. Identify the Angles in Triangle ABD:
- Triangle ABD has:
- Angle A = α (common)
- Angle B = 90° (given)
- Angle D = θ (since angle D is the remaining angle in triangle ABD)
- Thus, the angles in triangle ABD are:
- Angle A = α
- Angle B = 90°
- Angle D = θ
3. Identify the Angles in Triangle CBD:
- Triangle CBD has:
- Angle C = θ (common)
- Angle B = 90° (given)
- Angle D = α (since angle D is the remaining angle in triangle CBD)
- Thus, the angles in triangle CBD are:
- Angle C = θ
- Angle B = 90°
- Angle D = α
4. Check Similarity of Triangles:
- Triangle BAD and Triangle CBD:
- Angle B (BAD) = Angle C (CBD) = 90°
- Angle A (BAD) = Angle D (CBD) = α
- Angle D (BAD) = Angle B (CBD) = θ
- Since two angles of triangle BAD are equal to two angles of triangle CBD, by AA (Angle-Angle) similarity criterion, triangle BAD is similar to triangle CBD.
- Triangle BAD and Triangle CAB:
- Angle B (BAD) = Angle C (CAB) = 90°
- Angle A (BAD) = Angle A (CAB) = α
- Angle D (BAD) = Angle B (CAB) = θ
- Again, by AA similarity criterion, triangle BAD is similar to triangle CAB.
- Triangle BAD and Triangle CAB (Repeated):
- This is the same comparison as above, confirming that triangle BAD is similar to triangle CAB.
5. Conclusion:
- All three statements are true:
- I. Triangle BAD is similar to triangle CBD.
- II. Triangle BAD is similar to triangle CAB.
- III. Triangle BAD is similar to triangle CAB (repeated).
- Therefore, the correct answer is that all statements are true.
Final Answer:
All statements I, II, and III are true.
---
- Given that angle ABC = 90°, we denote angle A as α and angle C as θ.
- Therefore, the angles in triangle ABC are:
- Angle A = α
- Angle B = 90°
- Angle C = θ
- Since the sum of angles in a triangle is 180°, we have:
α+90°+θ=180°
This implies:
α+θ=90°
- Triangle ABD has:
- Angle A = α (common)
- Angle B = 90° (given)
- Angle D = θ (since angle D is the remaining angle in triangle ABD)
- Thus, the angles in triangle ABD are:
- Angle A = α
- Angle B = 90°
- Angle D = θ
- Triangle CBD has:
- Angle C = θ (common)
- Angle B = 90° (given)
- Angle D = α (since angle D is the remaining angle in triangle CBD)
- Thus, the angles in triangle CBD are:
- Angle C = θ
- Angle B = 90°
- Angle D = α
- Triangle BAD and Triangle CBD:
- Angle B (BAD) = Angle C (CBD) = 90°
- Angle A (BAD) = Angle D (CBD) = α
- Angle D (BAD) = Angle B (CBD) = θ
- Since two angles of triangle BAD are equal to two angles of triangle CBD, by AA (Angle-Angle) similarity criterion, triangle BAD is similar to triangle CBD.
- Triangle BAD and Triangle CAB:
- Angle B (BAD) = Angle C (CAB) = 90°
- Angle A (BAD) = Angle A (CAB) = α
- Angle D (BAD) = Angle B (CAB) = θ
- Again, by AA similarity criterion, triangle BAD is similar to triangle CAB.
- This is the same comparison as above, confirming that triangle BAD is similar to triangle CAB.
- All three statements are true:
- I. Triangle BAD is similar to triangle CBD.
- II. Triangle BAD is similar to triangle CAB.
- III. Triangle BAD is similar to triangle CAB (repeated).
- Therefore, the correct answer is that all statements are true.
All statements I, II, and III are true.
Topper's Solved these Questions
Similar Questions
Knowledge Check
ABC is a triangle in which ∠ABC=90∘,BD is perpendicular to AC. Which of the following is TRUE?
I. Triangle BAD is similar to triangle CBD.
II. Triangle BAD is similar to triangle CAB.
III. Triangle BAD is similar to triangle CAB.AOnly IBOnly II and IIICOnly I and IIIDAll I, II and IIIWhich of the following is true in a triangle ABC
A(b+c)sinB−C2=2acosA2B(b+c)cosA2=2asinB−C2C(b−c)cosA2=asinB−C2D(b−c)sinB−C2=2acosA2In ΔABC, which of the following is not true ?
 A−−→AB+−−→BC+−−→CA=→0B−−→AB+−−→BC−−−→AC=→0C−−→AB+−−→BC−−−→CA=→0D−−→AB−−−→CB+−−→CA=→0
A−−→AB+−−→BC+−−→CA=→0B−−→AB+−−→BC−−−→AC=→0C−−→AB+−−→BC−−−→CA=→0D−−→AB−−−→CB+−−→CA=→0
Which of the following is the property of similar triangle?
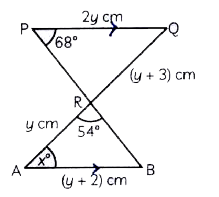
View SolutionGiven that △PQR is similar to △BAR, find the value of x:
View SolutionIn triangle ABC, which of the following is not true :

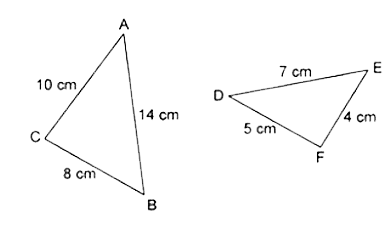
View SolutionWhich of [he following condition is TRUE about the similarity of triangle ABC and DEF given below?
View SolutionWhich of the following option is CORRECT for SAS similarity criterion for the triangle ABC and DEF?
View Solution