In given figure, a rectangle ABCD is inside a circle. Side AB is greater than BC. The ratio of area of circle to rectangle aBCD is π:√3 Line segment AE intersect CD at E where ∠OAB=∠EAD . Find the ratio of AE to AD .
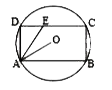
1:√2
1:√3
1:2
1:2√2
Step by step video & image solution for In given figure, a rectangle ABCD is inside a circle. Side AB is greater than BC. The ratio of area of circle to rectangle aBCD is pi:sqrt(3) Line segment AE intersect CD at E where angleOAB=angleEAD . Find the ratio of AE to AD . by Maths experts to help you in doubts & scoring excellent marks in Class 14 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
In the figure ABCD is a rectangle with AE = EF = FB, the ratio of the areas of triangle CEF and that of rectangle ABCD is

View SolutionThe figure shows the rectangle ABCD with a semicircle inscribed inside it as shown. What is the ratio of the area of the circle to that of the semicircle?

View Solution
Knowledge Check
The figure shows a rectangle ABCD with a semi-circle and a circle inscribed inside it as shown. What is the ratio of the area of the circle to that of the semi-circle ?
 A(√2−1)2B2(√2−1)2C(√2−1)2D2(√2−1)4
A(√2−1)2B2(√2−1)2C(√2−1)2D2(√2−1)4Pipe K fills a tank in 30 minutes. Pipe L can fill the same tank 5 times as fast as pipe K. If both the pipes were kept open when the tank is empty, how much time will it take for the tank to overflow ?
AA) 3 minutesBB) 2 minutesCC) 4 minutesDD) 5 minutesIn the given figure, ABCD is a rectangle inscribed in a quadrant of a circle of radius 10 cm. If AD=√25 cm then area of the rectangle is
 A32cm2B40cm2C44cm2D48cm2
A32cm2B40cm2C44cm2D48cm2
In the following figure, a rectangle ABCD enclosed three circles. If BC=14cm, find the area of the shaded portion
View SolutionSee the figure and find the ratio of :
Number of circles to all the figures inside the rectangle.
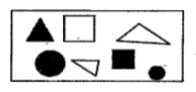
View SolutionIn rectangle ABCD, E is the midpoint of side BC. Prove that, AE = DE.
View SolutionSee the figure and find the ratio of
Number of circles to all the figures inside the rectangle.

View Solution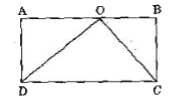
In the figure given above, the area of rectangle ABCD is 100 square cm, O is any point on AB and CD = 20 cm. Then the area of triangle COD ia
View Solution