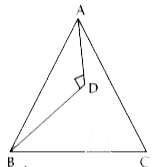
In the figure given below, ABC is a triangle with AB = 9, AC = 11 and E is the mid point of BC, AD bisects ∠BAC and ∠ADB=90∘. Find the length of DE.
1
2
3
2.5
Step by step video & image solution for In the figure given below, ABC is a triangle with AB = 9, AC = 11 and E is the mid point of BC, AD bisects angleBAC and angleADB=90^(@). Find the length of DE. by Maths experts to help you in doubts & scoring excellent marks in Class 14 exams.
Topper's Solved these Questions
Similar Questions
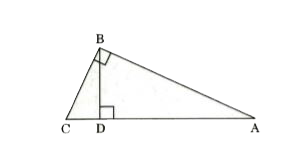
In the figure given below, ABC is a triangle with AB perpendicular to BC. Further BD is perpendicular to AC. If AD = 9 cm and DC = 4 cm, then what is the length of BD ?
 View Solution
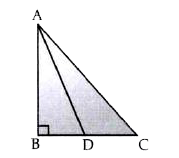
View SolutionIn the given figure ABC is a right angled triangle with ∠B=90∘ . D is the mid -point of BC . Show that AC2=AD2+3CD2 .
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
In a △ABC,AB = AC and AD⊥BC, then :
AAB<ADBAB>ADCAB=ADDAB≤AD - Question 2 - Select One
In the figure given below ∠BAC=90∘ and AD ⊥ BC. Then
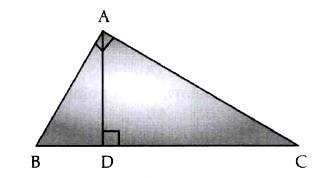 ABC×CD=AC2BAB×AC=BC2CBD×CD=AD2DAB×AC=AD2
ABC×CD=AC2BAB×AC=BC2CBD×CD=AD2DAB×AC=AD2 - Question 3 - Select One
If in a triangle AB=a,AC=b and D,E are the mid-points of AB and AC respectively, then DE is equal to
Aa4−b4Ba2−b2Cb4−a4Db2−a2
In the given triangle, AB=12 cm , AC=15 cm and AD=6 cm.BC//DE.Find the length of AE.
View SolutionIn ΔABC,AB=AC and D is a point in BC so that BD=CD. Prove that AD bisects ∠BAC.
View SolutionIn the given Fig. 3, in ΔABC,DandE are the mid point of the sides AB and AC respectively. Find the length of DE. Prove that DE=12BC.
 View Solution
View Solution
In the figure above, ABC is a triangle in which BC=24 cm and AC=13 cm. If AD is the perpendicular bisector of BC, then find the length of AD.View SolutionArea of ΔABC=30cm2. D and E are the mid - points of BC and AB respectively. Find A(ΔBDE) :
View Solution

