In triangle ABC, points D and E are on BC and AC respectively. If AD and BE intersect at point F so that AF : FD = 4 : 1 and BD : DC = 2 : 1, than find the ratio BF : BE?
11:15
15:11
7:8
9:11
To solve the problem step by step, we will use the concept of mass points in geometry.
1. Understanding the Ratios:
- We are given that AF:FD=4:1. This means that if we assign a mass of 1 to point D, then point A will have a mass of 4 (since the mass is inversely proportional to the segment lengths).
- Therefore, the total mass at point F (which is the intersection of AD and BE) will be 4+1=5.
2. Assigning Masses:
- Let’s assign masses based on the ratios:
- Mass at A = 4
- Mass at D = 1
- Total mass at F = 5
3. Using the Second Ratio:
- Now, we have the ratio BD:DC=2:1. This means if we assign a mass of 1 to point C, then point B will have a mass of 2 (again, since the mass is inversely proportional to the segment lengths).
- Therefore, the total mass at point D will be 2+1=3.
4. Finding the Mass at Point B:
- We already assigned a mass of 1 to point C and a mass of 2 to point B. Thus, the mass at D (which is the sum of the masses at B and C) should be equal to 3. This confirms our assignments are consistent.
5. Finding the Mass at Point E:
- Now, we have the mass at D as 1 (from point A) and 3 (from points B and C). To maintain balance, we can consider point E. Since point E is on AC, we need to find the mass at E that balances the system.
- The mass at E can be calculated as follows:
- Total mass at D = 3 (from B and C)
- Total mass at A = 4
- Therefore, mass at E = 4 (from A) + 3 (from B and C) = 7.
6. Calculating the Ratio BF : BE:
- Now, we can find the ratio BF:BE.
- The mass at B is 2 and the mass at E is 7. The ratio BF:BE is inversely proportional to the masses at E and B.
- Therefore, BF:BE=mass at E:mass at B=7:2.
Final Answer:
Thus, the ratio BF:BE=7:2.
- We are given that AF:FD=4:1. This means that if we assign a mass of 1 to point D, then point A will have a mass of 4 (since the mass is inversely proportional to the segment lengths).
- Therefore, the total mass at point F (which is the intersection of AD and BE) will be 4+1=5.
- Let’s assign masses based on the ratios:
- Mass at A = 4
- Mass at D = 1
- Total mass at F = 5
- Now, we have the ratio BD:DC=2:1. This means if we assign a mass of 1 to point C, then point B will have a mass of 2 (again, since the mass is inversely proportional to the segment lengths).
- Therefore, the total mass at point D will be 2+1=3.
- We already assigned a mass of 1 to point C and a mass of 2 to point B. Thus, the mass at D (which is the sum of the masses at B and C) should be equal to 3. This confirms our assignments are consistent.
- Now, we have the mass at D as 1 (from point A) and 3 (from points B and C). To maintain balance, we can consider point E. Since point E is on AC, we need to find the mass at E that balances the system.
- The mass at E can be calculated as follows:
- Total mass at D = 3 (from B and C)
- Total mass at A = 4
- Therefore, mass at E = 4 (from A) + 3 (from B and C) = 7.
- Now, we can find the ratio BF:BE.
- The mass at B is 2 and the mass at E is 7. The ratio BF:BE is inversely proportional to the masses at E and B.
- Therefore, BF:BE=mass at E:mass at B=7:2.
Thus, the ratio BF:BE=7:2.
Topper's Solved these Questions
Similar Questions
Knowledge Check
In a triangle ABC, D, E and F are the mid-points of the sides BC, CA and AB, respectively. BE and DF intersect at X. DE and CF intersect at Y. Find XY=?
A)12BC
B)14BC
C)13BC
D)23BCA12BCB14BCC13BCD23BCIn the triangle given below, D and E are mid points of AF and AG respectively. F and G are mid points of AB and AC respectively. If DE = 2.4 cm. then BC is equal to:
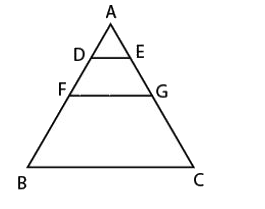 A4.8 cmB3.6 cmC9.6 cmD7.2 cm
A4.8 cmB3.6 cmC9.6 cmD7.2 cmIn a ΔABC, D and E are two points on AB and AC respectively, and DE ∥ BC. If the length of AD and AB is 5 cm and 10 cm respectively, then find the ratio between the area of ΔABC and area of Quadrilateral DECB.
A4:1B3:5C4:3D5:2
In a triangle ABC,DandE are points on BCandAC, respectivley, such that BD=2DCandAE=3EC. Let P be the point of intersection of ADandBE. Find BP/PE using the vector method.
View SolutionIn a triangle ABC, points D and E are on segments BC and AC such that BD= 3DC and AE= 4EC. Point P is on line ED such that D is the midpoint of segment EP. Lines AP and BC intersect at point S, Find the ratio BS/SD
View SolutionIn triangle ABC, if AD⊥BC and AD2=BD⋅DC. Then find the angle BAC
View SolutionIn triangle ABC, D and E are two points on the sides AB and AC respectively so that DE||BC and AD/BD=3/4 . The ratio of the area of △ABC to the area of trapezium DECB is:
त्रिभुज ABC में, AB और AC भुजाओं पर 2 बिंदु क्रमशः D और E इस तरह है कि DE||BC और AD/BD=3/4 है| △ABC क्षेत्रफल का समलंब चतुर्भुज DECB के क्षेत्रफल से अनुपात है :
View SolutionIn triangle ABC, D and E are two points on the sides AB and AC respectively so that DE || BC and AD/BD =3/4 .The ratio of the area of △ABC to the area of trapezium DECB is :
त्रिभुज ABC में,D और E क्रमशः भुजा AB और AC पर स्थित ऐसे बिंदु है कि DE ||BC है और AD/BD =3/4 है | त्रिभुज ABC के क्षेत्रफल तथा समलम्ब DECB के क्षेत्रफल में अनुपात ज्ञात करें |
View Solution

