ABC is a triangle with sides 3, 4, 5. Let P be a point inside the ΔABC, and let x, y and z be the length of peripendicular dropped from P on side AB, BC and AC respectively. What can be the maximum value of X+Y+Z.
1
2
3
4
To find the maximum value of X+Y+Z, where X,Y,Z are the lengths of the perpendiculars dropped from point P inside triangle ABC onto sides AB,BC, and AC respectively, we can use the following steps:
Step 1: Understand the triangle
Triangle ABC has sides of lengths 3,4, and 5. This is a right triangle with AB=4, AC=3, and BC=5.
Step 2: Calculate the area of triangle ABC
The area A of triangle ABC can be calculated using the formula for the area of a right triangle:
A=12×base×height
Here, we can take AB as the base and AC as the height:
A=12×4×3=6
Step 3: Relate the area to the perpendiculars
The area of triangle ABC can also be expressed in terms of the perpendiculars dropped from point P:
A=12×AB×X+12×BC×Y+12×AC×Z
Substituting the lengths of the sides:
6=12×4×X+12×5×Y+12×3×Z
This simplifies to:
6=2X+2.5Y+1.5Z
Step 4: Rearranging the equation
To find X+Y+Z, we can rearrange the equation:
12=4X+5Y+3Z
Step 5: Use the Cauchy-Schwarz inequality
To maximize X+Y+Z, we can apply the Cauchy-Schwarz inequality:
(X+Y+Z)(4+5+3)≥(2X+2.5Y+1.5Z)2
This gives:
(X+Y+Z)(12)≥(12)2
Thus:
X+Y+Z≥14412=12
Step 6: Finding the maximum value
The maximum value of X+Y+Z occurs when the equality in Cauchy-Schwarz holds, which happens when:
X4=Y5=Z3
Let k be the common ratio:
X=4k,Y=5k,Z=3k
Substituting into the area equation:
12=4(4k)+5(5k)+3(3k)=16k+25k+9k=50k
Thus:
k=1250=625
Now substituting back to find X,Y,Z:
X=4×625=2425,Y=5×625=3025,Z=3×625=1825
Calculating X+Y+Z:
X+Y+Z=2425+3025+1825=7225=2.88
Conclusion
The maximum value of X+Y+Z is 12.
Triangle ABC has sides of lengths 3,4, and 5. This is a right triangle with AB=4, AC=3, and BC=5.
The area A of triangle ABC can be calculated using the formula for the area of a right triangle:
A=12×base×height
Here, we can take AB as the base and AC as the height:
A=12×4×3=6
The area of triangle ABC can also be expressed in terms of the perpendiculars dropped from point P:
A=12×AB×X+12×BC×Y+12×AC×Z
Substituting the lengths of the sides:
6=12×4×X+12×5×Y+12×3×Z
This simplifies to:
6=2X+2.5Y+1.5Z
To find X+Y+Z, we can rearrange the equation:
12=4X+5Y+3Z
To maximize X+Y+Z, we can apply the Cauchy-Schwarz inequality:
(X+Y+Z)(4+5+3)≥(2X+2.5Y+1.5Z)2
This gives:
(X+Y+Z)(12)≥(12)2
Thus:
X+Y+Z≥14412=12
The maximum value of X+Y+Z occurs when the equality in Cauchy-Schwarz holds, which happens when:
X4=Y5=Z3
Let k be the common ratio:
X=4k,Y=5k,Z=3k
Substituting into the area equation:
12=4(4k)+5(5k)+3(3k)=16k+25k+9k=50k
Thus:
k=1250=625
Now substituting back to find X,Y,Z:
X=4×625=2425,Y=5×625=3025,Z=3×625=1825
Calculating X+Y+Z:
X+Y+Z=2425+3025+1825=7225=2.88
The maximum value of X+Y+Z is 12.
Topper's Solved these Questions
Similar Questions
Let ΔABC be an equilateral triangle with each side 2√3. Let P be a point outside the triangle such that the points A and P lie in the opposite sides of the straight line BC. Let PD, PE, PF be the perpendicular dropped on the sides BC, AC and AB respectively where D, foot of the perpendicular, lies inside the line segment BC. Let PD=2 what is the value of PE+PF.
View SolutionThe equations of sides AB, BC and AC of ΔABC are respectively y=x, y=0 and 4x+3y=12, then find :
(i) length of perpendicular from B to AC
(ii)∠BAC.
View Solution
Knowledge Check
Let D, E and F be the middle points of the sides BC,CA and AB respectively of a triangle ABC. Then, AD + BE + CF equals to
A0B0C2DNone of theseD is any point on side AC of ΔABC. If P,Q, X, Y are the mid points of AB,BC,ADandDCrespectively, then the ratio of PXandQYis
A1:2B1:1C2:1D2:3Let 'l' is the length of median from the vertex A to the side BC of a ΔABC. Then
A4l2=2b2+2c2−a2B4l2=b2+c2+2bccosAC4l2=a2+4bccosAD4l2=(2s−a)2sin2A2
the equation of perpendicular bisectors of side AB,BC of triangle ABC are x−y=5,x+2y=0 respectively and A(1,−2) then coordinate of C
View SolutionIf ΔABC is a equilateral triangle and P, Q, R are mid-points of sides AB, BC and CA respectively then-
View SolutionLet ABC be a triangle with equations of the sides AB,BCandCA respectively x−2=0,y−5=0and5x+2y−10=0. Then the orthocentre of the triangle lies on the line
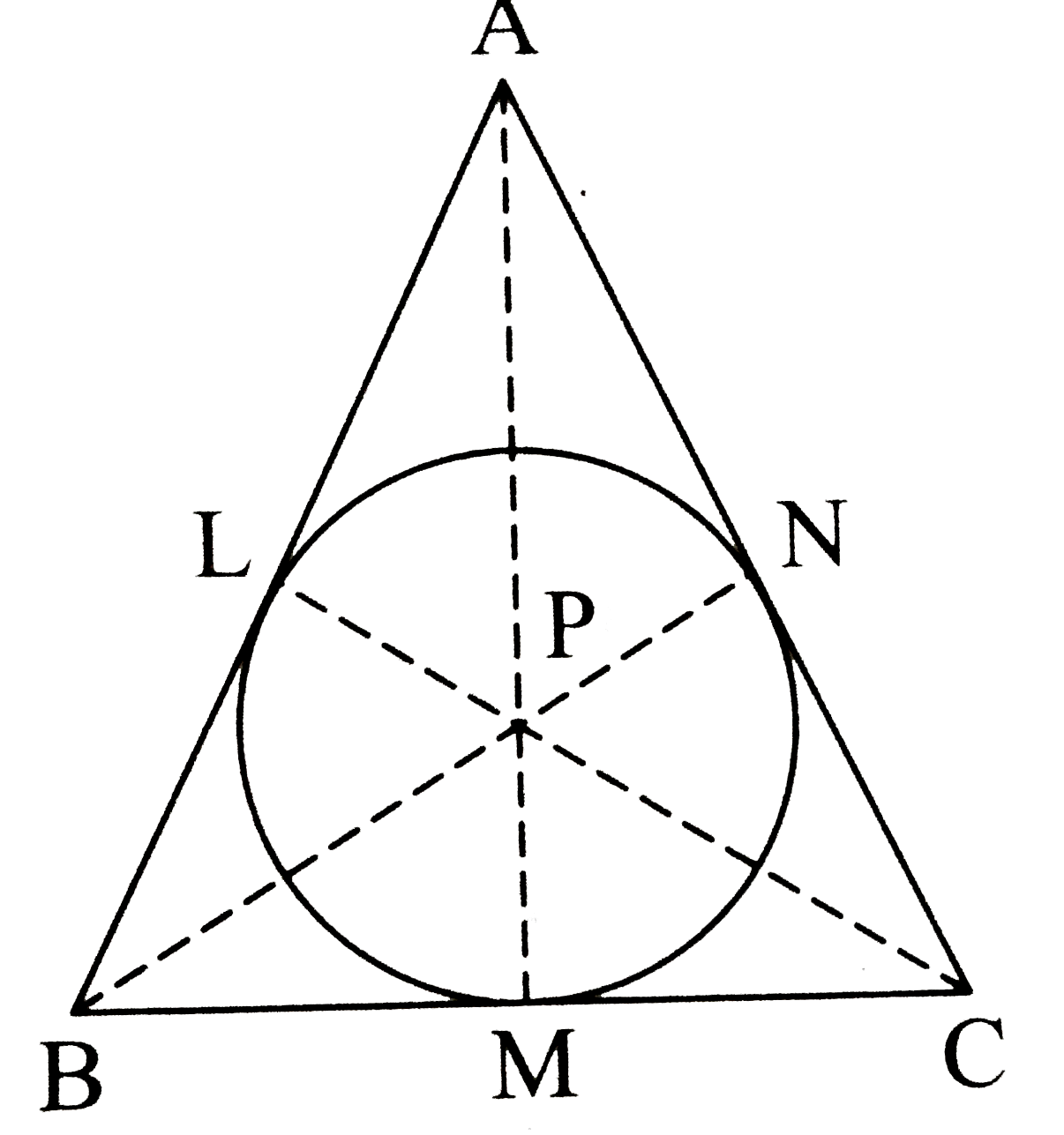
View SolutionA circle with centre P is inscribed in the ΔABC Side AB, side BC and side A C touch the circle at points L,M and N respectively . Prove that :
A(ΔABC)=12(AB+BC+AC)×r
View SolutionLet ABC is be a fixed triangle and P be veriable point in the plane of triangle ABC. Suppose a,b,c are lengths of sides BC,CA,AB opposite to angles A,B,C, respectively. If a(PA)2+b(PB)2+c(PC)2 is minimum, then point P with respect to ΔABC is
View Solution
