In ΔABC AD is perpendicular on side BC if AD2=BD. CD find ∠BAC.
60∘
90∘
30∘
45∘
To solve the problem, we need to find the angle ∠BAC in triangle ABC where AD is perpendicular to side BC and AD2=BD⋅CD.
1. Understanding the Triangle: We have triangle ABC with AD perpendicular to BC. This means that ∠ADB and ∠ADC are both 90∘.
2. Applying the Pythagorean Theorem: In triangle ABD:
AB2=AD2+BD2
In triangle ADC:
AC2=AD2+DC2
3. Substituting the Given Condition: We know from the problem that AD2=BD⋅CD. We can substitute AD2 in both equations:
- For triangle ABD:
AB2=BD⋅CD+BD2
- For triangle ADC:
AC2=BD⋅CD+DC2
4. Rearranging the Equations:
- From triangle ABD:
AB2=BD⋅(CD+BD)
- From triangle ADC:
AC2=CD⋅(BD+DC)
5. Combining the Results: Now, we add the two equations:
AB2+AC2=BD⋅(CD+BD)+CD⋅(BD+DC)
6. Factoring Out Common Terms: Notice that BD+DC=BC:
AB2+AC2=BC⋅(BD+CD)
7. Using the Given Condition: Since AD2=BD⋅CD, we can rewrite the equation:
AB2+AC2=BC2
8. Applying the Converse of the Pythagorean Theorem: According to the converse of the Pythagorean theorem, if AB2+AC2=BC2, then ∠BAC must be 90∘.
9. Conclusion: Therefore, we conclude that:
∠BAC=90∘
AB2=AD2+BD2
In triangle ADC:
AC2=AD2+DC2
- For triangle ABD:
AB2=BD⋅CD+BD2
- For triangle ADC:
AC2=BD⋅CD+DC2
- From triangle ABD:
AB2=BD⋅(CD+BD)
- From triangle ADC:
AC2=CD⋅(BD+DC)
AB2+AC2=BD⋅(CD+BD)+CD⋅(BD+DC)
AB2+AC2=BC⋅(BD+CD)
AB2+AC2=BC2
∠BAC=90∘
Topper's Solved these Questions
Similar Questions
Knowledge Check
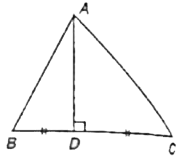
In the adjoning figure of ΔABC,AD is the perpendicular bisector of side BC. The triangle ABC is :
 Aright angledBisoscelesCscaleneDequilateral
Aright angledBisoscelesCscaleneDequilateralIn ΔABC,∠BAC=90∘andAD is drawn perpendicular to BC . If BD -=7 cm and CD = 28 cm , what is the length (in cm ) of Ad ?
A3.5B7C10.5D14
ABC is right angle triangle where AD is perpendicular on hypotenuse BC. If AC = 2 AB find BD.
View SolutionIn ΔABC, the bisector AD of ∠A is perpendicular to side BC (see figure). Show that AB =AC or ΔABC is isosceles.

View SolutionΔABC is an acute angle triangle. AD is perpendiculra on BC and DB = 3 CD. Find BC2-
View SolutionIn ΔABC, perpendicular drawn from point A meets BC at points D. If AD2=BD. DC then which of the following is correct.
View SolutionIn triangle ABC , ∠BAC=90∘ and AB=AC. Seg AP is perpendicular to side BC. D is any point on side BC. Prove that 2(AD)2=(BD)2+(CD)2
View SolutionIn ΔABC, ∠A is right angle and AD is perpendicular to BC. If AD=4cm,BC=12cm, then value of (cotB+cotC)=
View Solution