The centre of the circle which passes through points A, B and C is 'O'. If ∠BAO=30∘,∠BCO=40∘and∠AOC=x∘. Then find the value of x.
a)70∘
b)140∘
c)210∘
d)280∘
To solve the problem, we will use the properties of angles in a circle and the relationship between angles at the center and angles at the circumference.
1. Identify the Given Angles:
- We know that ∠BAO=30∘ and ∠BCO=40∘.
- We need to find ∠AOC=x∘.
2. Draw the Diagram:
- Draw a circle with center O and points A, B, and C on the circumference.
- Mark the angles ∠BAO and ∠BCO as given.
3. Identify Radii:
- Since O is the center of the circle, the segments OA, OB, and OC are all radii of the circle. Therefore, OA=OB=OC.
4. Use Isosceles Triangle Properties:
- In triangle OAB, since OA=OB, we have ∠OAB=∠OBA=30∘.
- Therefore, ∠AOB=180∘−(30∘+30∘)=120∘.
5. In Triangle OBC:
- Similarly, in triangle OBC, since OB=OC, we have ∠OBC=∠OCB=40∘.
- Therefore, ∠BOC=180∘−(40∘+40∘)=100∘.
6. Relate Angles at the Center and Circumference:
- The angle at the center ∠AOC can be found by adding the angles ∠AOB and ∠BOC:
∠AOC=∠AOB+∠BOC=120∘+100∘=220∘.
7. Final Calculation:
- However, we need to find x which is the angle ∠AOC.
- Since ∠AOC is the angle at the center, we can use the relationship:
∠AOC=2×∠ABC.
- From our earlier calculations, we found that ∠ABC=70∘ (since ∠AOB+∠BOC=120∘+100∘=220∘).
- Thus, x=2×70∘=140∘.
Conclusion:
The value of x is 140∘.
- We know that ∠BAO=30∘ and ∠BCO=40∘.
- We need to find ∠AOC=x∘.
- Draw a circle with center O and points A, B, and C on the circumference.
- Mark the angles ∠BAO and ∠BCO as given.
- Since O is the center of the circle, the segments OA, OB, and OC are all radii of the circle. Therefore, OA=OB=OC.
- In triangle OAB, since OA=OB, we have ∠OAB=∠OBA=30∘.
- Therefore, ∠AOB=180∘−(30∘+30∘)=120∘.
- Similarly, in triangle OBC, since OB=OC, we have ∠OBC=∠OCB=40∘.
- Therefore, ∠BOC=180∘−(40∘+40∘)=100∘.
- The angle at the center ∠AOC can be found by adding the angles ∠AOB and ∠BOC:
∠AOC=∠AOB+∠BOC=120∘+100∘=220∘.
- However, we need to find x which is the angle ∠AOC.
- Since ∠AOC is the angle at the center, we can use the relationship:
∠AOC=2×∠ABC.
- From our earlier calculations, we found that ∠ABC=70∘ (since ∠AOB+∠BOC=120∘+100∘=220∘).
- Thus, x=2×70∘=140∘.
The value of x is 140∘.
Topper's Solved these Questions
Similar Questions
Knowledge Check
'O' is the centre of the circle, line segment BOD is the angle bisector of ∠AOC,∠COD=50∘. Find ∠ABC :
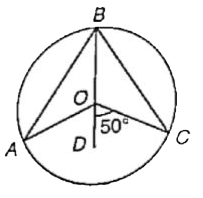 A25∘B50∘C100∘D120∘
A25∘B50∘C100∘D120∘In the given figure, O is the centre of cirlce. If ∠BAO=35∘and∠BCO=45∘ then the value of x will be
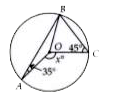 A160B170C80D140
A160B170C80D140In the given figure, O is the centre of the circle. If ∠BAO=30∘ and ∠BCO=50∘ , then ∠AOC is equal to:
 A60∘B80∘C40∘D160∘
A60∘B80∘C40∘D160∘
Find the equation of the circle which passes through the two points (6,4),(8,-4) and has centre on the X-axis
View SolutionFind the equation of the circle which passes through the points (3,7), (5,5) and has its centre on the line x−4y=1.
View SolutionThe centre of a circle passing through the points (0, 0), (1, 0) and touching the circle x2+y2=9, is
View SolutionFind the equation of a circle which passes through the origin and whose centre is (a,b).
View SolutionO is the centre of the circle ∠BCO=30∘ then find x and y
View Solution