ABCD is a rhombus, AB is extended to F and BA to E such that AB = AE = BF then what is the result?
ED>CF
ED⊥CF
ED2+CF2=EF2
ED∣∣CF
To solve the problem, we will follow these steps:
Step 1: Understand the properties of the rhombus
A rhombus is a quadrilateral with all sides equal in length. Therefore, in rhombus ABCD, we have:
- AB = BC = CD = DA
Step 2: Extend the sides
We extend side AB to point F and side BA to point E such that:
- AB = AE = BF
Let's denote the length of AB as x. This means:
- AE = x
- BF = x
Step 3: Analyze the angles
Since ABCD is a rhombus, the opposite angles are equal, and adjacent angles are supplementary. Let:
- Angle A = angle C = α
- Angle B = angle D = β
From the properties of a rhombus, we know:
- α+β=180∘
Step 4: Identify angles in triangles
Now, consider triangle AED and triangle BCF:
- In triangle AED, angle A is α and angle E is x.
- In triangle BCF, angle B is β and angle F is y.
Step 5: Use exterior angle theorem
For triangle AED:
- The exterior angle at point D (which is angle E + angle D) is equal to the sum of the opposite interior angles:
- Therefore, angle D = angle A + angle E = α+x
For triangle BCF:
- The exterior angle at point C (which is angle F + angle C) is equal to the sum of the opposite interior angles:
- Therefore, angle C = angle B + angle F = β+y
Step 6: Set up equations
From the properties of the angles in the rhombus:
- 2α+2β=180∘
- Therefore, α+β=90∘
Step 7: Conclude the relationship between ED and CF
Since we have established that:
- α+β=90∘
This means that the lines ED and CF are perpendicular to each other.
Final Result
Thus, the conclusion is:
- ED is perpendicular to CF.
A rhombus is a quadrilateral with all sides equal in length. Therefore, in rhombus ABCD, we have:
- AB = BC = CD = DA
We extend side AB to point F and side BA to point E such that:
- AB = AE = BF
- AE = x
- BF = x
Since ABCD is a rhombus, the opposite angles are equal, and adjacent angles are supplementary. Let:
- Angle A = angle C = α
- Angle B = angle D = β
- α+β=180∘
Now, consider triangle AED and triangle BCF:
- In triangle AED, angle A is α and angle E is x.
- In triangle BCF, angle B is β and angle F is y.
For triangle AED:
- The exterior angle at point D (which is angle E + angle D) is equal to the sum of the opposite interior angles:
- Therefore, angle D = angle A + angle E = α+x
- The exterior angle at point C (which is angle F + angle C) is equal to the sum of the opposite interior angles:
- Therefore, angle C = angle B + angle F = β+y
From the properties of the angles in the rhombus:
- 2α+2β=180∘
- Therefore, α+β=90∘
Since we have established that:
- α+β=90∘
This means that the lines ED and CF are perpendicular to each other.
Thus, the conclusion is:
- ED is perpendicular to CF.
Topper's Solved these Questions
Similar Questions
Knowledge Check
ABCD is a rhombus, AB is extended to F and BA to E such that AB = AE = BF then what is the result?
AED2+CF2=EF2BED/CFCED>CFDED1CFABCD is a rhombus, AB is extended to F and BA to E such that AB = AE = BF then what is the result?
AED>CFBEDI_CFCED2+CF2=EF2DED∣∣CFIn the given figure, Here, ABCD is a parallellogram in which DC is extended to F such that AF intersects BC at E.
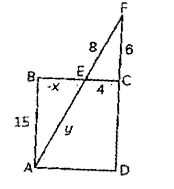
Perimeter of ΔABE=A35cmB36cmC40cmD45cm
ABCD is a rhombus. RABS is a straight line such that RA = AB = BS. Prove that RD and SC when produced meet at right angles.
View SolutionABCD is a parallelogram. E is a point on extended side AB such that AB = BE. By joining D to E it intersects side BC at P. Find length of PC if BC = 15 cm.
View SolutionABCD is a rhombus in which the altitude from D to side AB bisects AB. Find the angles of the rhombus.
View SolutionABCD is a rhombus in which altitude from D to side AB bisects AB. Find the angles of the rhombus.
View SolutionABCD is a parallelogram. E is a point on BA such that BE=2EA and F is a point on Do such that DF=2 FC. Prove that AE CF is a parallelogram whose area is one third area of parallelogram AB CD
View Solution
