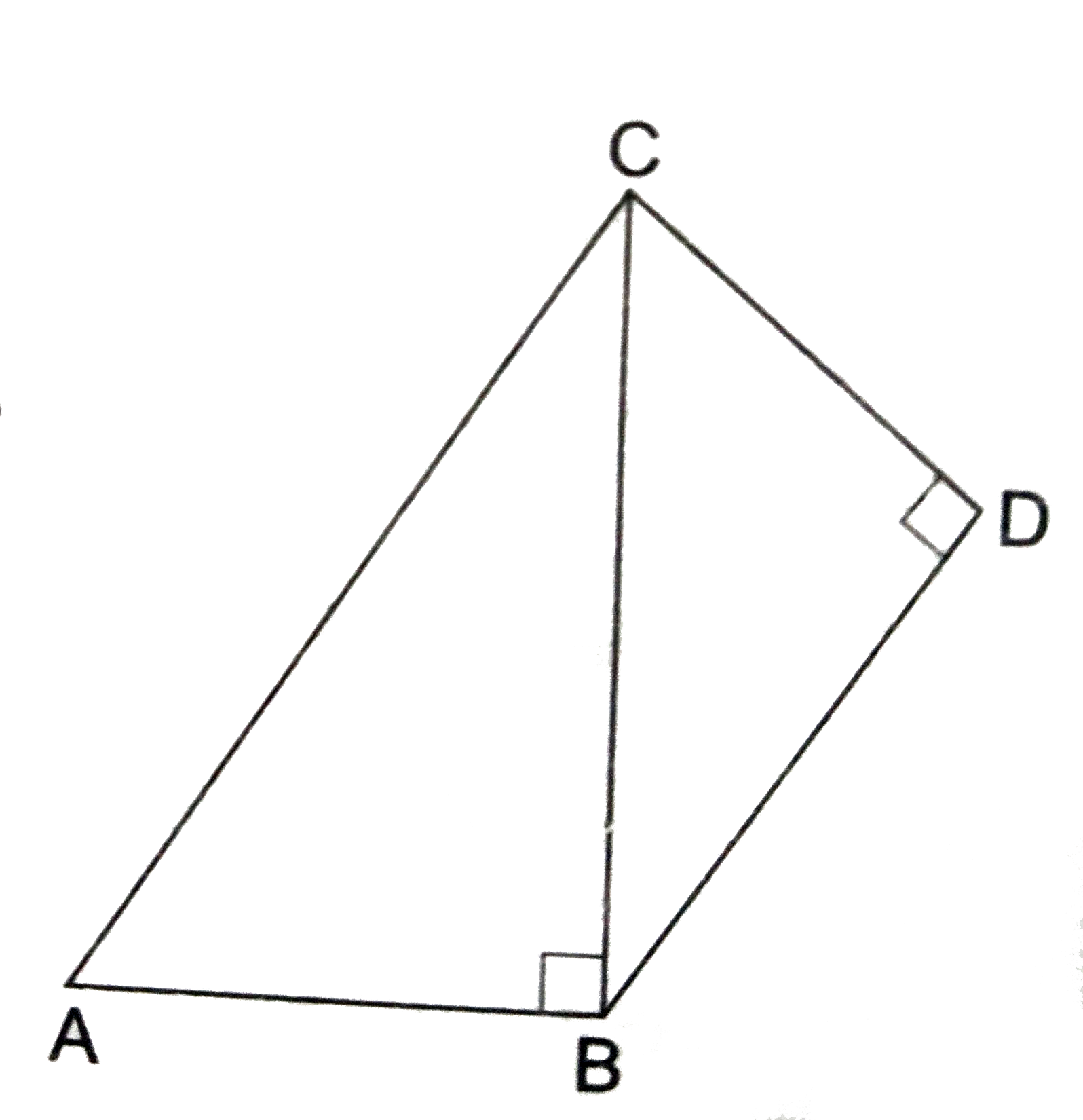
AOBD is a quadrilateral in which ∠AOB=∠ABD=90∘and∠DAB=60∘. If OA = 3 cm, OB = 4 cm then what is the area of quadrilateral AOBD.
6+52√3cm2
6+25√32cm2
6+√3cm2
6+25√3cm2
To find the area of quadrilateral AOBD, we will break it down into two triangles: triangle AOB and triangle ABD.
Step 1: Draw the Quadrilateral
First, we will sketch the quadrilateral AOBD based on the given angles and lengths:
- AOB is a right triangle with angle AOB = 90°.
- ABD is also a right triangle with angle ABD = 90°.
- Angle DAB = 60°.
Step 2: Identify the Lengths
We know:
- OA = 3 cm
- OB = 4 cm
Step 3: Calculate the Length of AB
Using the Pythagorean theorem in triangle AOB:
AB=√OA2+OB2=√32+42=√9+16=√25=5 cm
Step 4: Calculate the Length of AD
In triangle ABD, we know:
- Angle DAB = 60°
- We can use the cosine function to find AD:
cos(60°)=ABAD
Substituting the known values:
12=5AD⟹AD=10 cm
Step 5: Calculate the Length of BD
Using the sine function in triangle ABD:
sin(60°)=BDAD
Substituting the known values:
√32=BD10⟹BD=10⋅√32=5√3 cm
Step 6: Calculate the Area of Triangle AOB
The area of triangle AOB can be calculated as:
AreaAOB=12×OA×OB=12×3×4=6 cm2
Step 7: Calculate the Area of Triangle ABD
The area of triangle ABD can be calculated as:
AreaABD=12×AB×BD=12×5×5√3=25√32 cm2
Step 8: Calculate the Total Area of Quadrilateral AOBD
Now, we can find the total area of quadrilateral AOBD by adding the areas of triangles AOB and ABD:
AreaAOBD=AreaAOB+AreaABD=6+25√32 cm2
Final Answer
Thus, the area of quadrilateral AOBD is:
AreaAOBD=6+25√32 cm2
First, we will sketch the quadrilateral AOBD based on the given angles and lengths:
- AOB is a right triangle with angle AOB = 90°.
- ABD is also a right triangle with angle ABD = 90°.
- Angle DAB = 60°.
We know:
- OA = 3 cm
- OB = 4 cm
Using the Pythagorean theorem in triangle AOB:
AB=√OA2+OB2=√32+42=√9+16=√25=5 cm
In triangle ABD, we know:
- Angle DAB = 60°
- We can use the cosine function to find AD:
cos(60°)=ABAD
Substituting the known values:
12=5AD⟹AD=10 cm
Using the sine function in triangle ABD:
sin(60°)=BDAD
Substituting the known values:
√32=BD10⟹BD=10⋅√32=5√3 cm
The area of triangle AOB can be calculated as:
AreaAOB=12×OA×OB=12×3×4=6 cm2
The area of triangle ABD can be calculated as:
AreaABD=12×AB×BD=12×5×5√3=25√32 cm2
Now, we can find the total area of quadrilateral AOBD by adding the areas of triangles AOB and ABD:
AreaAOBD=AreaAOB+AreaABD=6+25√32 cm2
Thus, the area of quadrilateral AOBD is:
AreaAOBD=6+25√32 cm2
Topper's Solved these Questions
Similar Questions
Knowledge Check
ABCD is a quadrilateral in which AB = 5 cm, CD = 8 cm and the sum of angle A and angle D is 180°. What is the name of this quadrilateral?
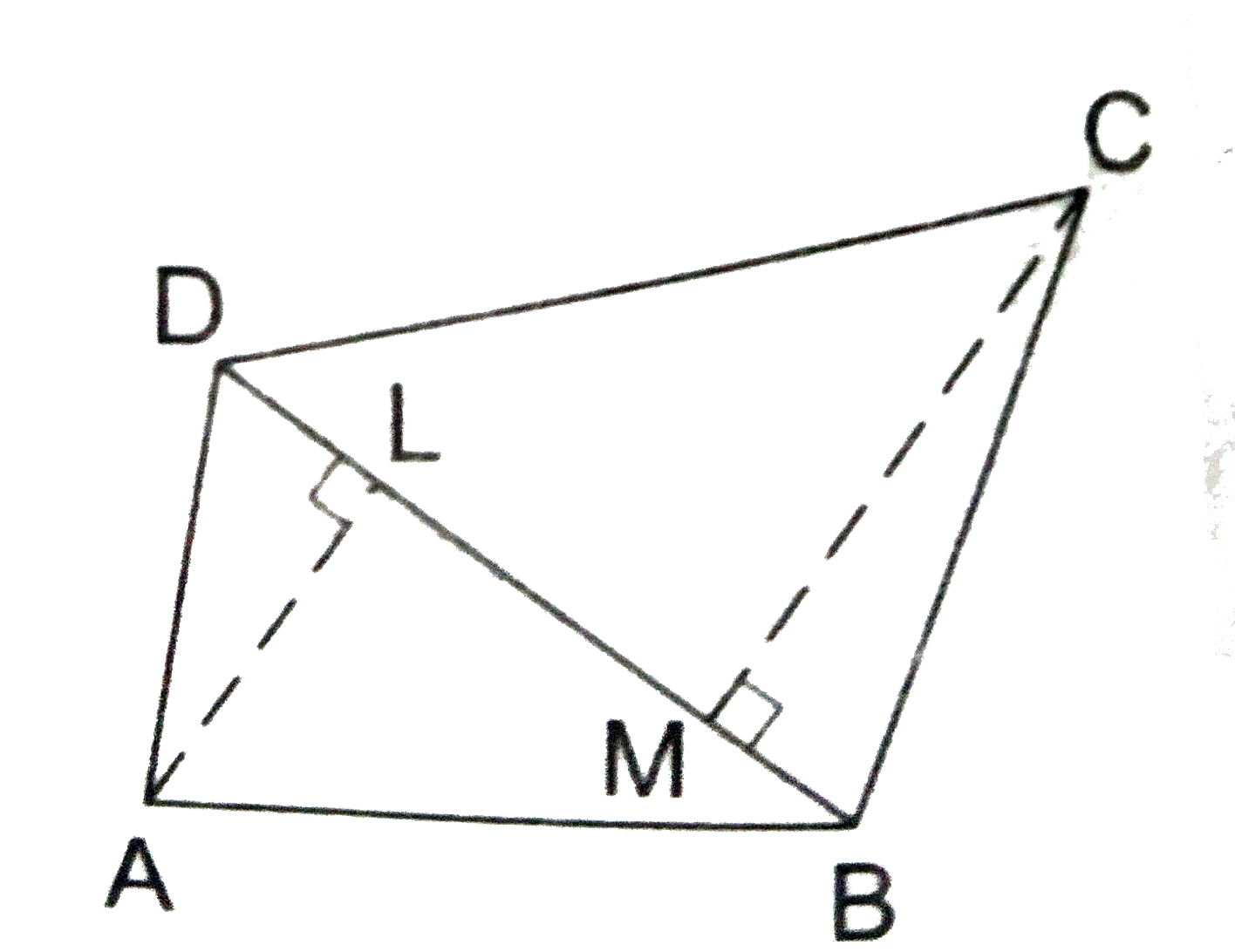
AParallelogramBTrapeziumCRhombusDCan not be determinedABCD is a quadrilateral in which diagonal BD = 64 cm. AL⊥BD and CM⊥BD, such that AL=13.2cm and CM=16.8cm. The area of the quadrilateral ABCD is square centimeters is :
Aa) 422.4Bb) 690.0Cc) 537.6Dd) 960.0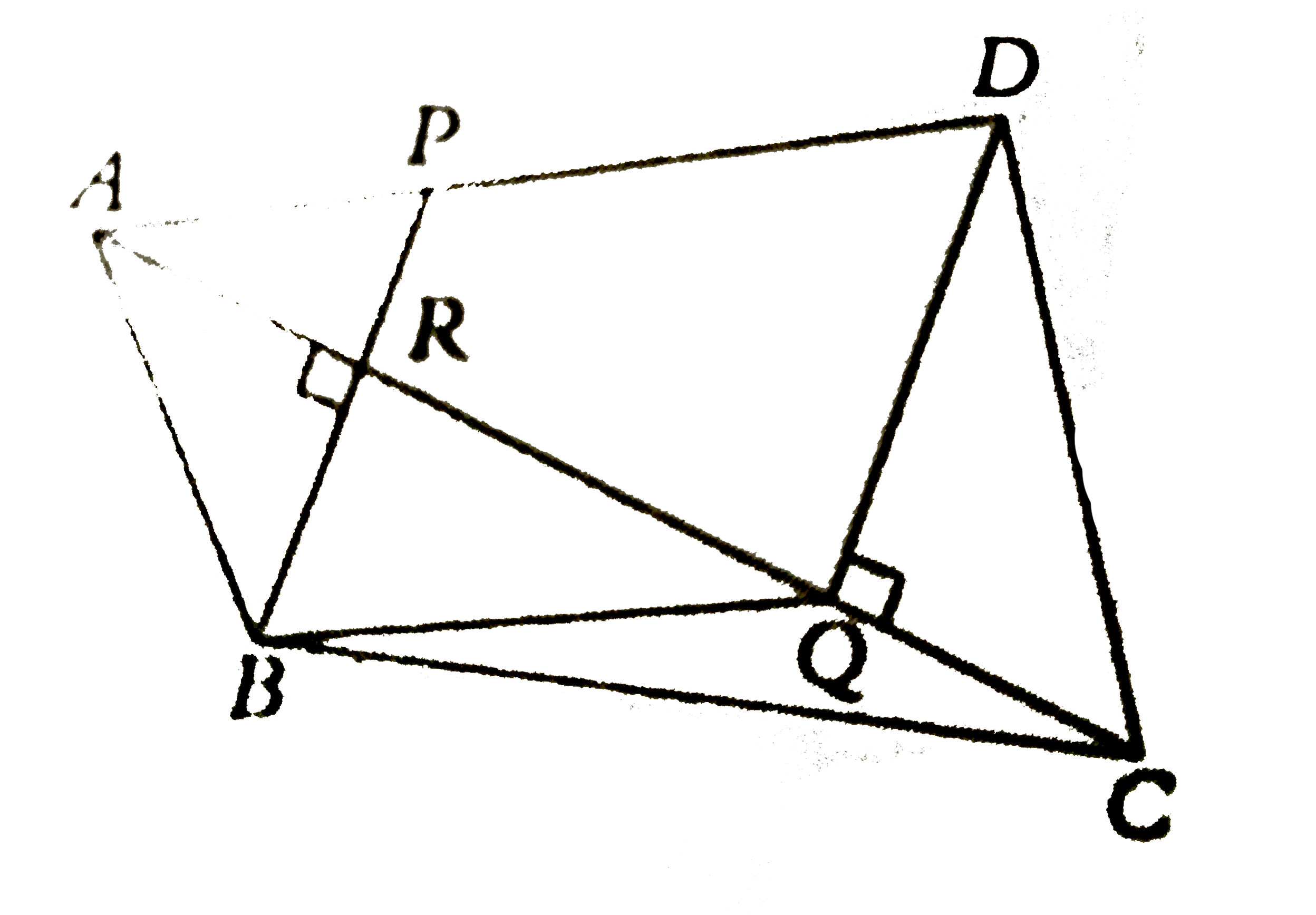
In the figure given above, ABCD is a quadrilateral and BPDQ is parallelogram. AR = 50 cm, CQ = 70 cm, BR = 60, and PR = 40 cm. If the area of the quadrilateral ABCD is 15,600cm2, then find the area of then find the area of the parallelogram BPDQ (in cm2).A9460B8460C7500D9000
ABCD is a quadrilateral with AB = 9 cm, BC = 40 cm, CD = 28 cm, DA = 15 cm and angle ABC is a right-angle.
What is the area of quadrilateral ABCD ?
View SolutionIn the given figure ABCD is a quadrilateral in which diagonal BD=24cm,AL⊥BDandCM⊥BD such that AL=9cm and CM=12 cm. Calculate the area of the quadrilateral .
View SolutionFind the area of quadrilateral ABCD in which ∠B=90∘, BC = 32 cm, AB = 24 cm and CD=DA = 25 cm.
View SolutionIn the given figure, PQRS is a quadrilateral. If QR = 18 cm and PS = 9 cm, then what is the area (in cm2) of quadrilateral PQRS?
View SolutionConstruct a quadrilateral ABCD in which AB=4.2 cm, ∠A=80∘,BC=2.4cm,CD=3.3cm and AD=2.4cm.
View Solution