Let two chords AB and AC of the larger circle having same centre touch the smaller circle having same centre at X and Y. Then XY = ?
BC
12BC
13BC
14BC
To solve the problem, we need to find the length of the line segment XY, which is formed by the points where the chords AB and AC of the larger circle touch the smaller circle. Here’s a step-by-step solution:
Step 1: Understand the Geometry
We have two circles with the same center O. The larger circle has chords AB and AC, while the smaller circle is tangent to these chords at points X and Y respectively.
Hint: Visualize the two circles and the chords. Identify the points of tangency.
Step 2: Identify the Properties of Tangents
When a tangent is drawn from a point to a circle, the radius to the point of tangency is perpendicular to the tangent. Thus, we have:
- OX ⊥ AB
- OY ⊥ AC
Hint: Remember that the radius at the point of tangency forms a right angle with the tangent line.
Step 3: Bisecting the Chords
Since OX is perpendicular to AB, it bisects the chord AB at point X. Therefore, we can say:
- AX = BX = 1/2 AB
Similarly, since OY is perpendicular to AC, it bisects the chord AC at point Y:
- AY = CY = 1/2 AC
Hint: Use the property of perpendicular bisectors to establish equal segments.
Step 4: Establish Similar Triangles
Now, we can look at triangles AXY and ABC. Since they share angle A, and we have established that AX = 1/2 AB and AY = 1/2 AC, we can conclude that:
- Triangle AXY is similar to triangle ABC (by the Angle-Angle similarity criterion).
Hint: Look for shared angles and proportional sides to establish similarity.
Step 5: Set Up the Ratio
From the similarity of triangles, we can set up the following ratio:
- AX / AB = AY / AC = XY / BC
Since AX = 1/2 AB and AY = 1/2 AC, we can express the ratios as:
- (1/2 AB) / AB = (1/2 AC) / AC = XY / BC
This simplifies to:
- 1/2 = 1/2 = XY / BC
Hint: Simplifying ratios can help you find relationships between the segments.
Step 6: Solve for XY
From the established ratio, we have:
- XY / BC = 1/2
Thus, we can express XY as:
- XY = (1/2) * BC
Hint: Use algebraic manipulation to isolate the variable you are solving for.
Conclusion
The length of segment XY is half the length of segment BC:
- XY = (1/2) BC
Final Answer
XY = 1/2 BC
We have two circles with the same center O. The larger circle has chords AB and AC, while the smaller circle is tangent to these chords at points X and Y respectively.
When a tangent is drawn from a point to a circle, the radius to the point of tangency is perpendicular to the tangent. Thus, we have:
- OX ⊥ AB
- OY ⊥ AC
Since OX is perpendicular to AB, it bisects the chord AB at point X. Therefore, we can say:
- AX = BX = 1/2 AB
- AY = CY = 1/2 AC
Now, we can look at triangles AXY and ABC. Since they share angle A, and we have established that AX = 1/2 AB and AY = 1/2 AC, we can conclude that:
- Triangle AXY is similar to triangle ABC (by the Angle-Angle similarity criterion).
From the similarity of triangles, we can set up the following ratio:
- AX / AB = AY / AC = XY / BC
- (1/2 AB) / AB = (1/2 AC) / AC = XY / BC
- 1/2 = 1/2 = XY / BC
From the established ratio, we have:
- XY / BC = 1/2
Thus, we can express XY as:
- XY = (1/2) * BC
The length of segment XY is half the length of segment BC:
- XY = (1/2) BC
XY = 1/2 BC
Topper's Solved these Questions
Similar Questions
Prove that in two concentric circles, the chord of the larger circle which touches the smaller circle is bisected at the point of contact.
View SolutionTwo circles are tangent internally at P and a chord, AB of the larger circle is tangent to the smaller circle at C. PB and PA cut the smaller circle at E and D, respectively. If AB = 15 cm, While PE = 2 cm and PD = 3 cm. Find AC
View Solution
Knowledge Check
Let two chords AB and AC of the larger circle having same centre touch the smaller circle having same centre at X and Y. Then XY = ?
ABCB12BCC13BCD14BCTwo concentric circles with centre P have radii 6.5 cm and 3.3 cm. Through a point A of the larger circle, a tangent is drawn to the smaller circle touching it at B and the larger circle at C. find the length of the tangent
A5.6 cmB11.2 cmC11.8 cmD6.5 cm
In the figure, two circles touch internally at point P. chord AB of the larger circle intersects the smaller circle in C and D. Prove ∠CPA≅∠DPB.
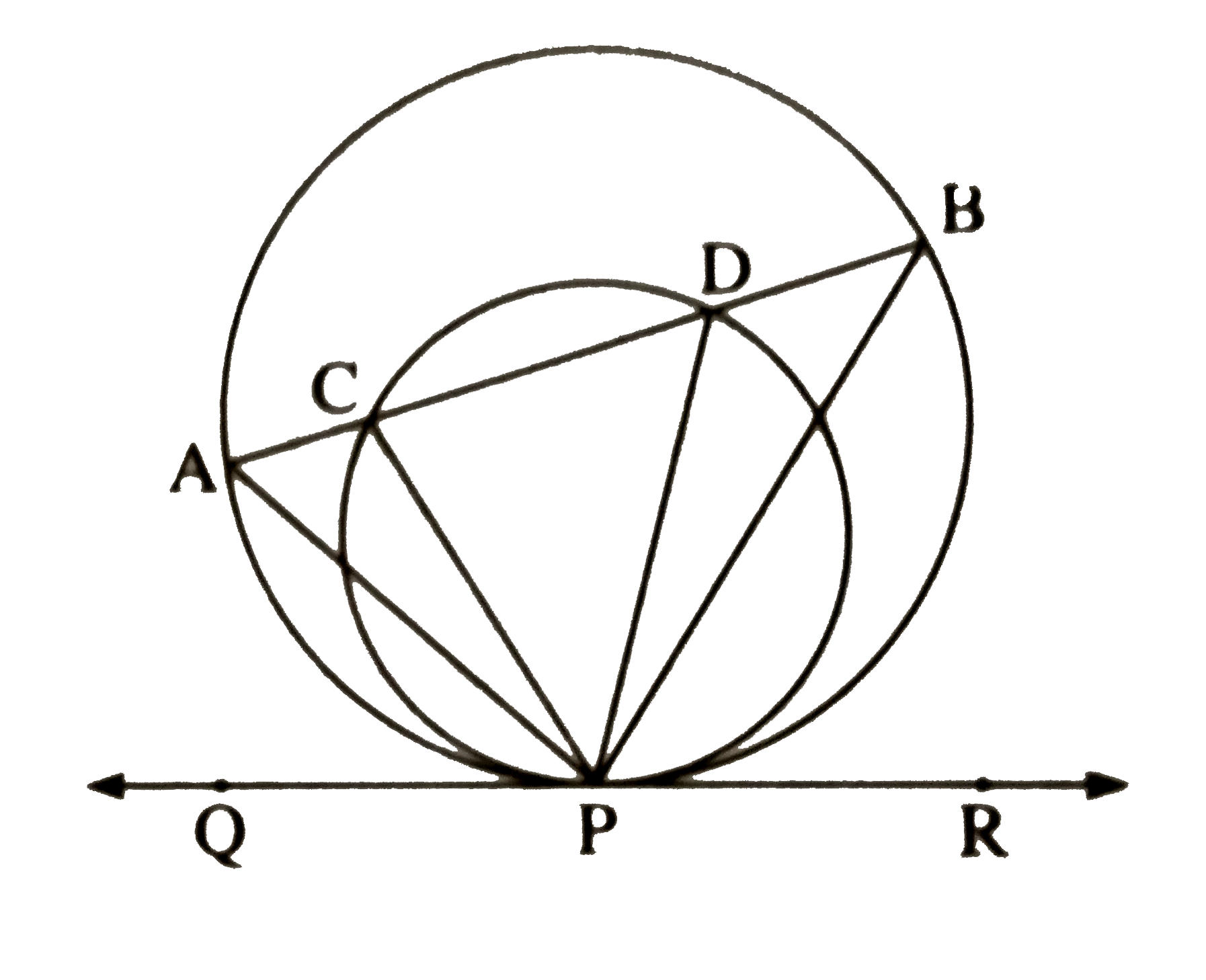
View SolutionTwo chords AB and AC of a circle are equal. Prove that the centre of the circle lies on the angle bisector of ∠BAC.
View SolutionProve that in two concentric circles, the chord of the larger circle, which touches the smaller circle, is bisected at the point of contact.
View SolutionTwo chord AB and AC of a circle are equal. Prove that the centre of a circle lies on the angle bisector of ∠BAC
View SolutionIn the figure, the radius of the larger circle is 2 cm and the radius of the smaller circle is 1 cm and the larger circle passes through the centre of the smaller circleThe length (in cm) of the chord AB is :
View SolutionIn two concentric circles, a chord of length 8cm of the larger circle touches the smaller circle. If the radius of the larger circle is 5cm then find the radius of the smaller circle.
View Solution
