PQ is a tangent to the circle at T. If TR = TS where R and S are points on the circle and ∠RST=65∘, the ∠PTS =
65∘
130∘
115∘
55∘
Step by step video & image solution for PQ is a tangent to the circle at T. If TR = TS where R and S are points on the circle and angleRST=65^(@), the anglePTS = by Maths experts to help you in doubts & scoring excellent marks in Class 14 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
In the figure above (not to scale), PQ is a tangent segment to the circle at P.If P,R,S and T are concyclic points, ∠QPR=40∘ and PR=RQ then find ∠PTS.
View SolutionProve that the length of the tangent drawn from an external point to a circle are equal. Using the above, do the following: TP and TQ are tangents from T to the circle with circle O and R in any point on the circle. If AB is a tangent to the circle at R, prove that TA + AR =TB +BR.

View Solution
Knowledge Check
PQ is a tangent to the circle at T. If TR = TS where R and S are points on the circle and ∠RST=65∘, the ∠PTS =
A65∘B130∘C115∘D55∘In the figure , PQ and PR are tangent to the circle with centre O. Also, S is a point on the circle such that ∠SQC=50∘and∠SRM=60∘, then ∠QSR=
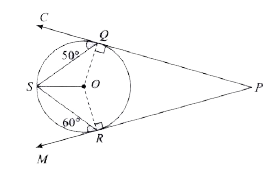 A40∘B70∘C80∘D45∘
A40∘B70∘C80∘D45∘PQ is tangent at a point R of the circle with centre O. If ST is a diameter of the circle and ∠TRQ=30∘ find ∠PRS
A30∘B60∘C45∘D120∘
The number of tangents that can be drawn to a circle at a point on the circle is
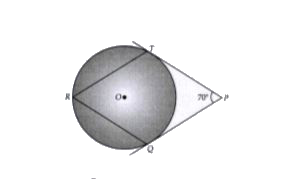
View SolutionIn figure, O is the centre of a circle. PT and PQ are tangents to the circle from an external point P. If ∠TPQ=70∘, find ∠TRQ.
View SolutionPQL and PRM are tangents to a circle with centre O at points Q and R respectively. S is a point on the circle such that ∠SQL=50∘ and ∠SRM=60∘. Find value of ∠QSR.
View SolutionPQRS is a square. SR is a tangent (at point S) to the circle with centre OandTR=OS. Then, the ratioof area of the circle to the area of the square is
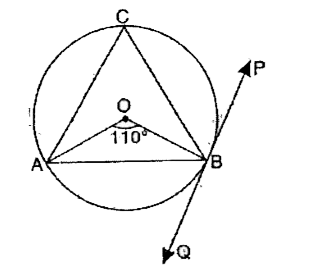
View SolutionIn the given figure, AB is a chord of the circle with centre O and PQ is a tangent at point B of the circle. If ∠AOB=110∘, then ∠ ABQ is
View Solution
