ABC is a triangle, PQ is line segment interseting AB in P and AC in Q and PQ||BC. The ratio of AP : BP = 3 : 5 and length of PQ is 18 cm. The length of BC is
28 cm
48 cm
84 cm
42 cm
To solve the problem step by step, we will use the information given in the question and apply Thales' theorem.
1. Understanding the Triangle and Ratios:
- We have triangle ABC.
- Line segment PQ intersects AB at point P and AC at point Q.
- It is given that PQ || BC.
- The ratio of AP to BP is given as 3:5.
2. Assigning Variables:
- Let AP = 3x and BP = 5x.
- Therefore, the total length of AB (AP + BP) = 3x + 5x = 8x.
3. Using Thales' Theorem:
- Since PQ is parallel to BC, Thales' theorem states that the ratios of the segments are equal:
APBP=AQQC=PQBC
- We already know:
APBP=3x5x=35
- We also know that PQ = 18 cm.
4. Setting Up the Equation:
- From Thales' theorem, we can set up the equation:
PQBC=35
- Substituting the known value of PQ:
18BC=35
5. Cross-Multiplying to Solve for BC:
- Cross-multiply to find BC:
3⋅BC=18⋅5
3⋅BC=90
BC=903=30 cm
Final Answer:
The length of BC is 30 cm.
---
- We have triangle ABC.
- Line segment PQ intersects AB at point P and AC at point Q.
- It is given that PQ || BC.
- The ratio of AP to BP is given as 3:5.
- Let AP = 3x and BP = 5x.
- Therefore, the total length of AB (AP + BP) = 3x + 5x = 8x.
- Since PQ is parallel to BC, Thales' theorem states that the ratios of the segments are equal:
APBP=AQQC=PQBC
- We already know:
APBP=3x5x=35
- We also know that PQ = 18 cm.
- From Thales' theorem, we can set up the equation:
PQBC=35
- Substituting the known value of PQ:
18BC=35
- Cross-multiply to find BC:
3⋅BC=18⋅5
3⋅BC=90
BC=903=30 cm
The length of BC is 30 cm.
Topper's Solved these Questions
Similar Questions
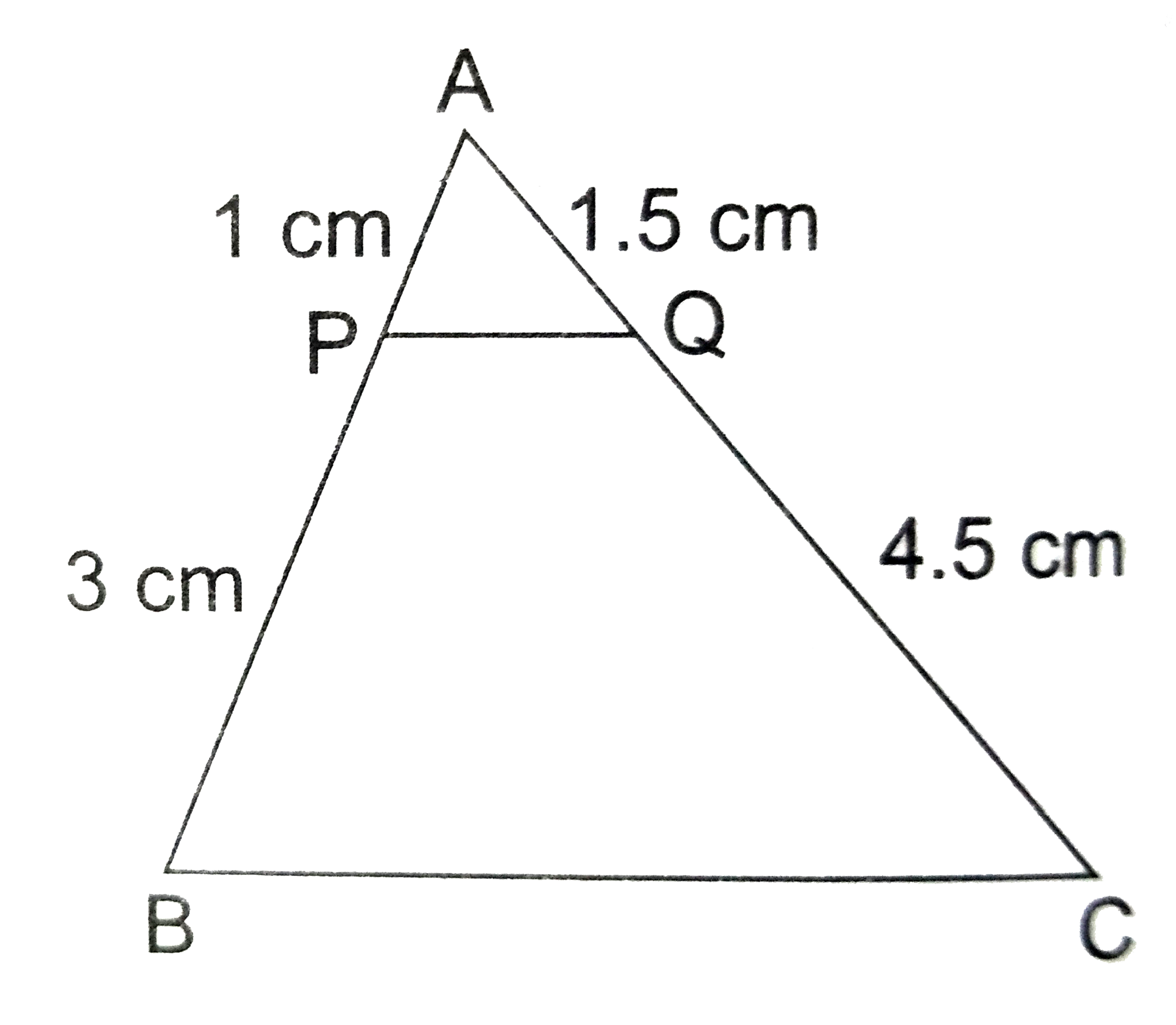
In the given figure, ABC is triangle and PQ is a stright line meeting AB in P and AC in Q. if AP=1cm,PB=3cm,AQ=1.5cm,QC=4.5cm prove that area of ΔAPQ is 116 of the area of ΔABC.
View SolutionIn ΔABC, PQ is a line segment which intersect AB on P and AC on Q so that PQ||BC and divides ΔABC in 2 equal parts of same area then find BPAB.
View Solution
Knowledge Check
△ABC is an isosceles triangle with AB=AC=15cm and altitude from A to BC is 12 cm. The length of sides BC is :
A9 cmB12 cmC18 cmD20 cmPoints P and Q lie on the sides AB and AC of triangle ABC respectivey such that line segment PQ is parallel to side BC. If the ratio of AP : PB is 1 : 4 and area of ΔAPQ is 4 square cm., what is the area of trapezium PQCB ?
A60 sq. cmB16 sq. cmC96 sq. cmD21 sq. cmIn ΔABC the straight line parallel to the side BCmeets ABandACat the points PandQ respectively. If AP=QC, the length of ABis 12 units and the length of AQis 2 units, then the length (in units) of CQ is
A4B6C8D10
Draw line segment PQ with the length 9cm.
View SolutionIn ABC , PQ is a line segment intersecting AB at P and AC at Q such that PQBC and PQ divides ABC into two parts equal in area. Find BPAB .
View SolutionB is a point on line segment AC such that AB: BC is 3 : 2. If AC = 40 cm, then length of BC is
View SolutionIn a △ABC P and Q are points on AB and AC respectively and PQ||BC. Prove that the median AD bisects PQ.
View SolutionInside a triangle ABC, a straight line parallel to BC intersects AB and AC at the point P and respectively. If AB=3PB, then PQ:BC is
View Solution
