Statement-1: The shape of an automobile is so designed that its front resembles the stream line pattern of the fluid through which is moves.
Statement-2: The shape of the automobile is made stream lines in order to reduced resistance offered by the fluid.
Statement-1, is true, Statement-2 is true, Statement-2 is correct explanation for statement-1
Statement-1 is true, statement-2 is true, statement-2 is NOT a correct explantion for statement-1
statement-1 is true, statement-2 is false
statement-1 is false statement-2 is true
The correct Answer is:A
To analyze the statements provided in the question, we can break down the reasoning step by step.
1. Understanding Statement 1:
- The first statement claims that the shape of an automobile is designed to resemble the streamline pattern of the fluid through which it moves.
- This means that the automobile's design is influenced by the way fluid (like air) flows around it, which is characterized by smooth, continuous lines without abrupt changes in direction.
2. Understanding Statement 2:
- The second statement asserts that the shape of the automobile is streamlined to reduce the resistance offered by the fluid.
- Streamlining refers to designing the automobile in such a way that it minimizes drag or air resistance when moving through the fluid (air). This is crucial for improving fuel efficiency and performance.
3. Analyzing the Relationship Between the Statements:
- Both statements are interrelated. The design that resembles the streamline pattern (Statement 1) inherently serves the purpose of reducing resistance (Statement 2).
- When an automobile is designed with a streamlined shape, it allows air to flow smoothly around it, thus minimizing turbulence and drag.
4. Conclusion:
- Since both statements are true and support each other, we can conclude that the correct option is that both statements are true.
Final Answer:
Both Statement 1 and Statement 2 are true.
---
- The first statement claims that the shape of an automobile is designed to resemble the streamline pattern of the fluid through which it moves.
- This means that the automobile's design is influenced by the way fluid (like air) flows around it, which is characterized by smooth, continuous lines without abrupt changes in direction.
- The second statement asserts that the shape of the automobile is streamlined to reduce the resistance offered by the fluid.
- Streamlining refers to designing the automobile in such a way that it minimizes drag or air resistance when moving through the fluid (air). This is crucial for improving fuel efficiency and performance.
- Both statements are interrelated. The design that resembles the streamline pattern (Statement 1) inherently serves the purpose of reducing resistance (Statement 2).
- When an automobile is designed with a streamlined shape, it allows air to flow smoothly around it, thus minimizing turbulence and drag.
- Since both statements are true and support each other, we can conclude that the correct option is that both statements are true.
Both Statement 1 and Statement 2 are true.
Topper's Solved these Questions
- BOOK - ALLENCHAPTER - ELASTICITY, SURFACE TENSION AND FLUID MECHANICSEXERCISE - Exercise 3 (Comprehension based questions)24videos
ELASTICITY, SURFACE TENSION AND FLUID MECHANICS
- BOOK - ALLENCHAPTER - ELASTICITY, SURFACE TENSION AND FLUID MECHANICSEXERCISE - Exercise 4 A (Elasticity)7videos
ELASTICITY, SURFACE TENSION AND FLUID MECHANICS
- BOOK - ALLENCHAPTER - ELASTICITY, SURFACE TENSION AND FLUID MECHANICSEXERCISE - Exercise 2 (One or more than one correct answer)53videos
ELASTICITY, SURFACE TENSION AND FLUID MECHANICS
- BOOK - ALLENCHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-V B19videos
CENTRE OF MASS
- BOOK - ALLENCHAPTER - ERROR AND MEASUREMENTEXERCISE - Part-2(Exercise-2)(B)22videos
ERROR AND MEASUREMENT
Similar Questions
This question contains Statement -1 and Stantement -2 Of the four choices given after the statements, choose the one that best desctibes the two statemesnts.
Statement -1:
For a mass M kept at the center of a cube of side 'a', the flux of gravitational field passing through its sides 4πGM.
Statement -2:
If the direction of a field due to a point source is radial and its dependence on the distance 'r' from the source is given as 1r2, its flux through a closed surface depends only on the strength of the source enclosed by the surface and not on the size or shape of the surface.View SolutionStatement-1 : It is not necessary for a particle to move in a circular path to define angular momentum. It can be defined about any point in space.
Statement-2 : Particle moving in a straight line has non-zero angular momentum about a point which is not lying on the path of the particle.View SolutionStatement-1: All chords of the curve 3x2−y2−2x+4y=0 which subtend a right angle at the origin pass through a fixed point.
Statement-2: The equation ax+by+c=0 represents a family of straight lines passing through a fixed point iff there is a linear relation between a, b and c.View SolutionStatement 1: The circumcircle of a triangle formed by the lines x=0,x+y+1=0 and x−y+1=0 also passes through the point (1, 0). Statement 2: The circumcircle of a triangle formed by three tangents of a parabola passes through its focus.
View SolutionViscosity is the property of fluid by virtue of which fluid offers resistance to deformation under the influence of a tangential force.
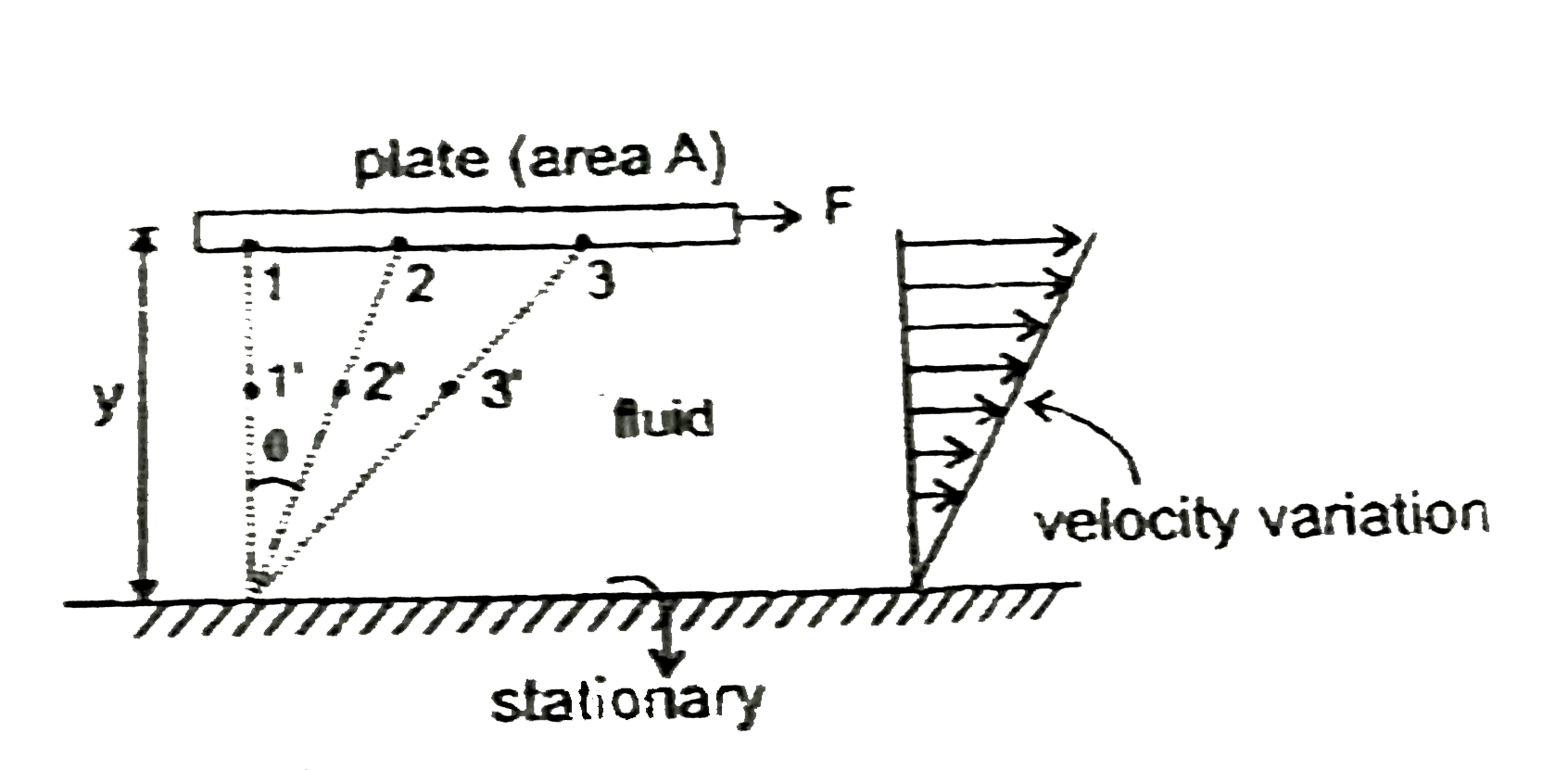
In the given figure as the the plate moves the fluid particle at the surface moves from position 1 to 2 and so on, but particles at the bottom boundry remain stationary. if the gap between palte and bottom boundary is small, fluid particles in between plate and bottom moves with velocities as shown by linear velocity distribution curve otherwise the velocity distribution may be parabolic. As per Newton's law of viscity the tangential force is related to time rate of deformation -
FAαd'θdt but y=d'θdt=u,d'θdt=uy
then F=ηAuy,η= coefficient of viscosity
for non-linear velocity distribution -
F=ηAdudy
where uy or dudy is known as velocity gradiant.
The velocity gradient just near the bottom boundary is equal to -View SolutionViscosity is the property of fluid by virtue of which fluid offers resistance to deformation under the influence of a tangential force.
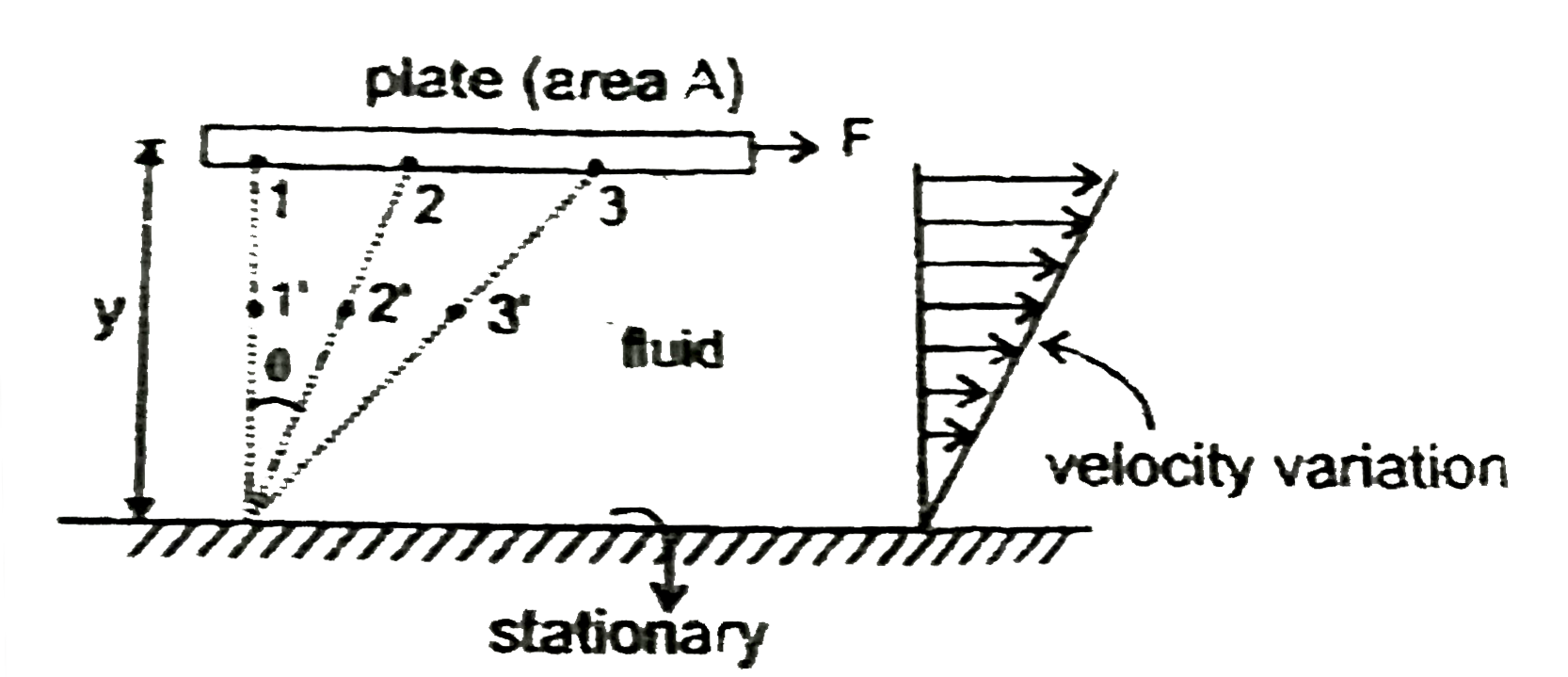
In the given figure as the the plate moves the fluid particle at the surface moves from position 1 to 2 and so on, but particles at the bottom boundry remain stationary. if the gap between palte and bottom boundary is small, fluid particles in between plate and bottom moves with velocities as shown by linear velocity distribution curve otherwise the velocity distribution may be parabolic. As per Newton's law of viscity the tangential force is related to time rate of deformation -
FAαd'θdt but y=d'θdt=u,d'θdt=uy
then F=ηAuy,η= coefficient of viscosity
for non-linear velocity distribution -
F=ηAdudy
where uy or dudy is known as velocity gradiant.
The velocity gradient just below the plate, in above problem is equal to - (per second)View SolutionViscosity is the property of fluid by virtue of which fluid offers resistance to deformation under the influence of a tangential force.
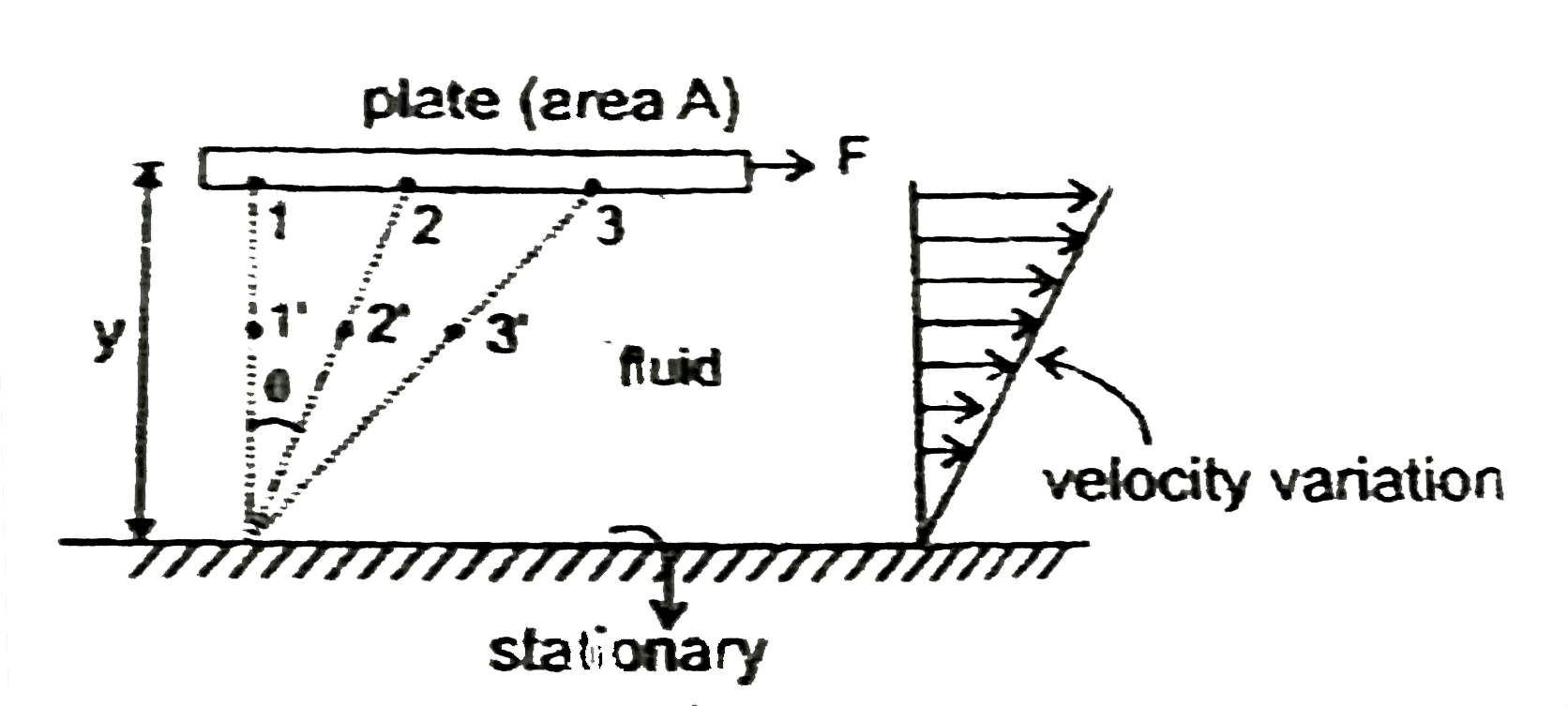
In the given figure as the the plate moves the fluid particle at the surface moves from position 1 to 2 and so on, but particles at the bottom boundry remain stationary. if the gap between palte and bottom boundary is small, fluid particles in between plate and bottom moves with velocities as shown by linear velocity distribution curve otherwise the velocity distribution may be parabolic. As per Newton's law of viscity the tangential force is related to time rate of deformation -
FAαd'θdt but y=d'θdt=u,d'θdt=uy
then F=ηAuy,η= coefficient of viscosity
for non-linear velocity distribution -
F=ηAdudy
where uy or dudy is known as velocity gradiant.
If velocity distribution is given as (parabolic)
u=c1y2+c2y+c3
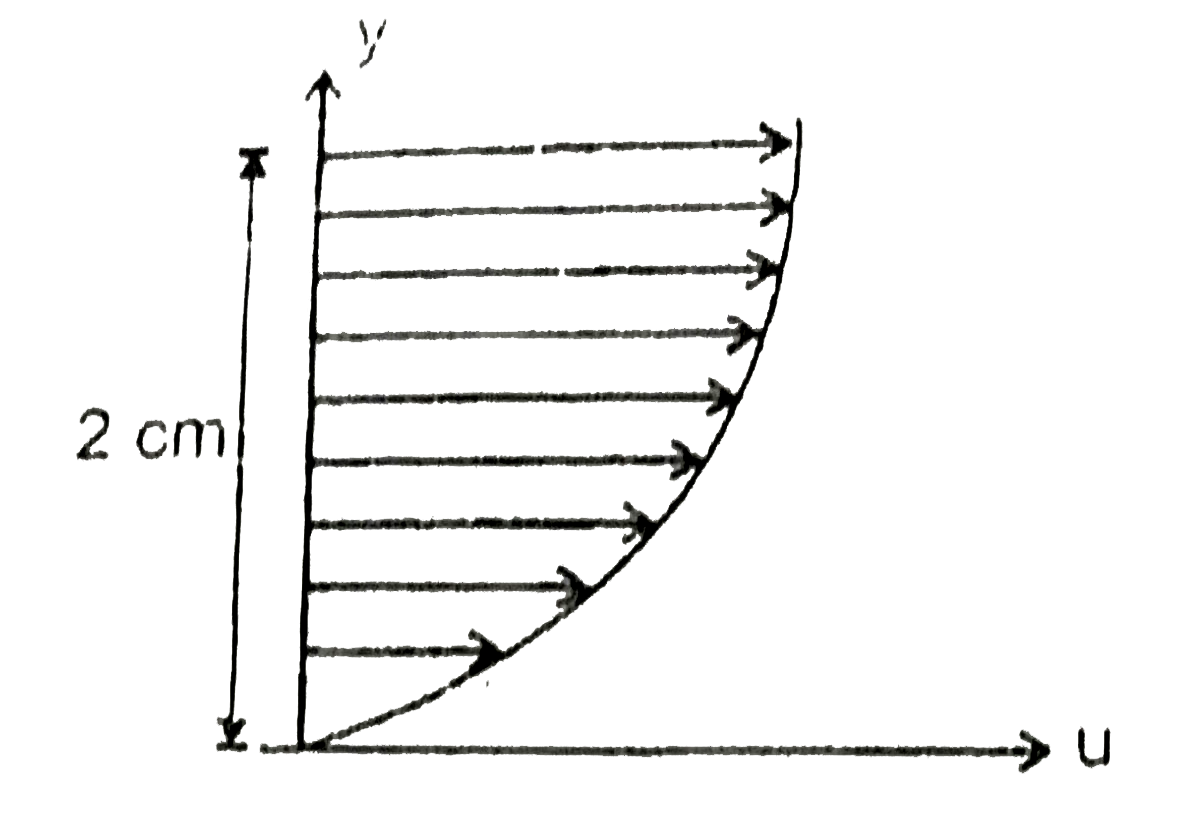For the same force of 2N and the speed of the plate 2m/sec, and area of plate is 1 and viscousity is .001, the constant C1,C2 & C3 are View SolutionWhen an object moves through a fluid, as when a ball falls through air or a glass sphere falls through water te fluid exerts a viscous foce F on the object this force tends to slow the object for a small sphere of radius r moving is given by stoke's law, Fw=6πηrv. in this formula η in the coefficient of viscosity of the fluid which is the proportionality constant that determines how much tangential force is required to move a fluid layer at a constant speed v, when the layer has an area A and is located a perpendicular distance z from and immobile surface. the magnitude of the force is given by F=ηAv/z. For a viscous fluid to move from location 2 to location 1 along 2 must exceed that at location 1, poiseuilles's law given the volumes flow rate Q that results from such a pressure difference P2−P1. The flow rate of expressed by the formula Q=πR4(P2−P1)8ηL poiseuille's law remains valid as long as the fluid flow is laminar. For a sfficiently high speed however the flow becomes turbulent flow is laminar as long as the reynolds number is less than approximately 2000. This number is given by the formula Re=2¯vρRη In which ¯v is the average speed ρ is the density η is the coefficient of viscosity of the fluid and R is the radius of the pipe. Take the density of water to be ρ=1000kg/m3
Q. If the sphere in previous question has mass of 1×10−5kg what is its terminal velocity when falling through water? (η=1×10−3Pa−s)
A. 1.3m/s
B. 3.4m/s
C. 5.2m/s
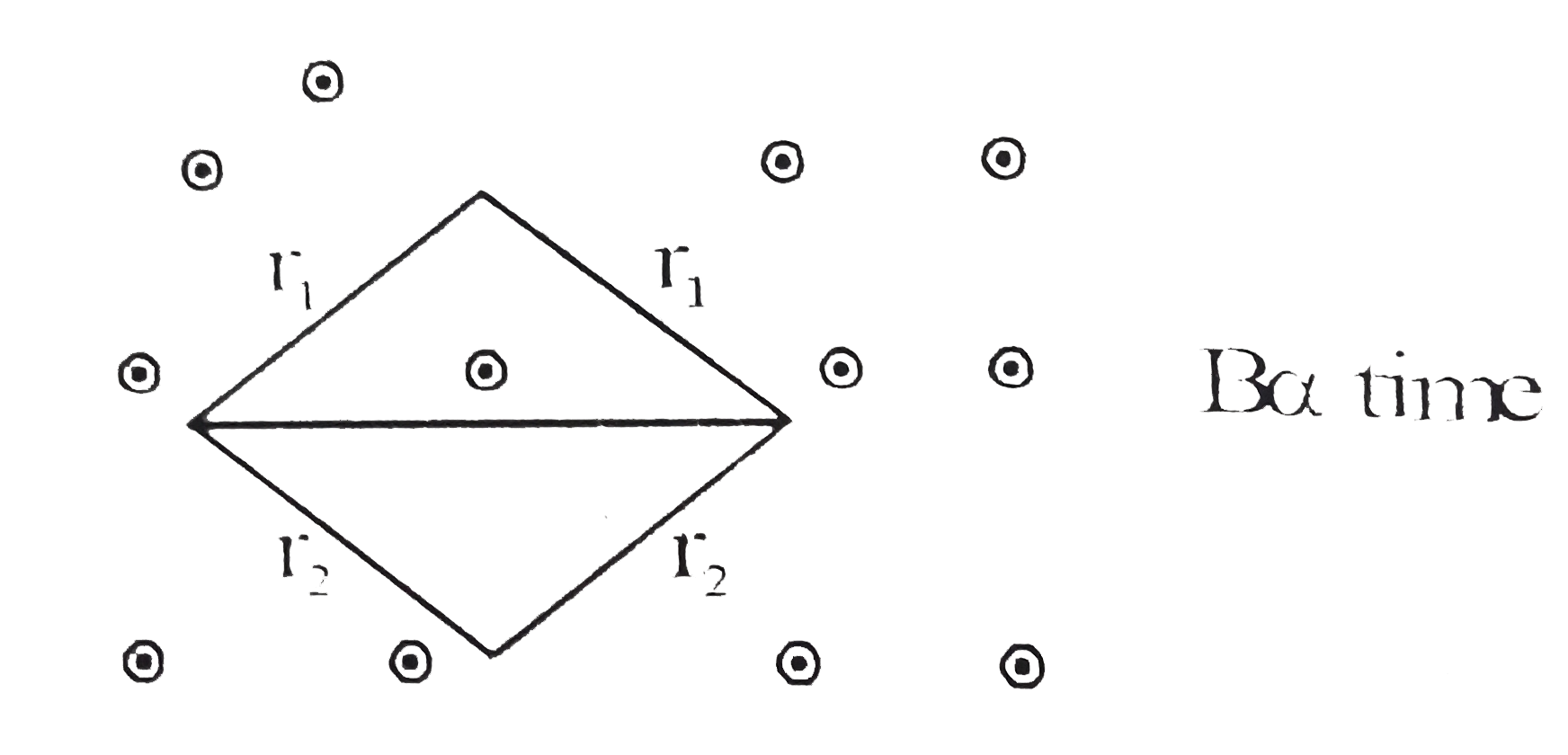
D. 6.5m/sView SolutionThe sides of a square shaped frame, Shown in the diagram are made of wires of resistances r1 and r2 The frame is places in a uniform magnetic field, which is perpendicular to the plane of figure and is increasing at a constant rate. The resistance that should be connected across the diagonal of frame, so that this wire is warmed up at greatest rate is given by R=nr1r2r1+r2. Find n.
View SolutionViscosity is the property of fluid by virtue of which fluid offers resistance to deformation under the influence of a tangential force.
In the given figure as the the plate moves the fluid particle at the surface moves from position 1 to 2 and so on, but particles at the bottom boundry remain stationary. if the gap between palte and bottom boundary is small, fluid particles in between plate and bottom moves with velocities as shown by linear velocity distribution curve otherwise the velocity distribution may be parabolic. As per Newton's law of viscity the tangential force is related to time rate of deformation -
FAαd'θdt but y=d'θdt=u,d'θdt=uy
then F=ηAuy,η= coefficient of viscosity
for non-linear velocity distribution -
F=ηAdudy
where uy or dudy is known as velocity gradiant.
In the given figure if force of 2N required to maintain constant velocity of plate, the value of constant C1,&C2 are -
View Solution