Assertion:- The magnitude of velocity of two boats relative to river is same. Both boats start simultaneously from same point on one bank They may reach opposite bank simultaneously moving along different straight line paths.
Reason:- For boats to cross the river in same time, the compnonet of their velocity relative to river in direction normal to flow should be same.
If both Assertion & Reason are True & the Reason is a correct explanation of the Assertion.
If both Assertion & Reason are True but Reason is not a correct explanation of the Assertion.
If Assertion is True but the Reason is False.
If both Assertion & Reason are False.
The correct Answer is:A
To solve the problem, we need to analyze the assertion and the reason given in the question.
Step 1: Understanding the Assertion
The assertion states that two boats can reach the opposite bank of a river simultaneously while moving along different straight paths, provided their velocities relative to the river are the same.
Step 2: Analyzing the Velocity Components
When the boats are crossing the river, their velocity can be broken down into two components:
- The component of velocity in the direction across the river (normal to the flow of the river).
- The component of velocity in the direction of the river's flow.
Step 3: Condition for Simultaneous Crossing
For both boats to reach the opposite bank at the same time, the component of their velocities that is directed across the river must be the same. This means that even if they are moving at different angles, as long as their vertical (y-axis) components of velocity are equal, they will take the same time to cross.
Step 4: Mathematical Representation
Let:
- v = magnitude of the velocity of each boat relative to the river.
- θ1 and θ2 = angles made by the boats with respect to the riverbank.
The vertical component of the velocity for each boat can be expressed as:
- For Boat 1: v1y=v⋅sin(θ1)
- For Boat 2: v2y=v⋅sin(θ2)
For both boats to cross the river in the same time T:
v⋅sin(θ1)=v⋅sin(θ2)
Step 5: Conclusion
Since the magnitudes of their velocities relative to the river are the same, and the components of their velocities in the direction normal to the flow of the river are also equal, both boats can indeed reach the opposite bank simultaneously despite following different paths.
Final Answer
Both the assertion and reason are true, and the reason correctly explains the assertion.
---
The assertion states that two boats can reach the opposite bank of a river simultaneously while moving along different straight paths, provided their velocities relative to the river are the same.
When the boats are crossing the river, their velocity can be broken down into two components:
- The component of velocity in the direction across the river (normal to the flow of the river).
- The component of velocity in the direction of the river's flow.
For both boats to reach the opposite bank at the same time, the component of their velocities that is directed across the river must be the same. This means that even if they are moving at different angles, as long as their vertical (y-axis) components of velocity are equal, they will take the same time to cross.
Let:
- v = magnitude of the velocity of each boat relative to the river.
- θ1 and θ2 = angles made by the boats with respect to the riverbank.
- For Boat 1: v1y=v⋅sin(θ1)
- For Boat 2: v2y=v⋅sin(θ2)
v⋅sin(θ1)=v⋅sin(θ2)
Since the magnitudes of their velocities relative to the river are the same, and the components of their velocities in the direction normal to the flow of the river are also equal, both boats can indeed reach the opposite bank simultaneously despite following different paths.
Both the assertion and reason are true, and the reason correctly explains the assertion.
Topper's Solved these Questions
- TEST PAPERSBOOK - ALLENCHAPTER - TEST PAPERSEXERCISE - PAPER 2
60 Videos
- TEST PAPERSBOOK - ALLENCHAPTER - TEST PAPERSEXERCISE - PAPER 3
99 Videos
- TEST PAPER 4BOOK - ALLENCHAPTER - TEST PAPER 4EXERCISE - PHYSICS
44 Videos
- UNIT & DIMENSIONS, BASIC MATHS AND VECTOR BOOK - ALLENCHAPTER - UNIT & DIMENSIONS, BASIC MATHS AND VECTOR EXERCISE - Exercise (J-A)
7 Videos
Similar Questions
Velocity of the boat with respect to river is 10m/s. From point A it is steered in the direction shown. Where will it reach on the opposite bank ?

View SolutionVelocity of a boat relative to river current and river current velocity are equal in magnitude. Starting from point A on the southern bank, the boatman wants to reach a point B on the nothern bank in north−east from A. In which direction he has to steer the boat?

View SolutionVelocity of the boat with respect to river is 10 m/s. From point A it is steered in the direction shown to reach point C. Find the time of the trip and distance between B and C

View SolutionThe current velocity of river grows in proportion to the distance from its bank and reaches the maximum value v0 in the middle. Near the banks the velocity is zero. A boat is moving along the river in such a manner that the boatman rows his boat always perpendicular to the current. The speed of the boat in still water is u. Find the distance through which the boat crossing the river will be carried away by the current, if the width of the river is c. Also determine the trajectory of the boat.
View SolutionThe velocity of water in a river is 2 kmph, while width is 400 m. A boat is rowed from a point rowing always aiming opposite point at 8 kmph of still water velocity. On reaching the opposite bank the drift obtained is
View SolutionA boat takes 4 hr upstream and 2 hr down the stream for covering the same distance. The ratio of velocity of boat to the water in river is
View SolutionA boat going down stream crosses a float at a point A. 't1' minutes later the boat reverses its direction and in the next 't2' minutes it crosses the float at a distance L from the point A. The velocity of the river is
View SolutionTwo train are moving in a straight line in the same direction with a speed of 80 km/h. The relative velocity of one trains w.r.t. each other is
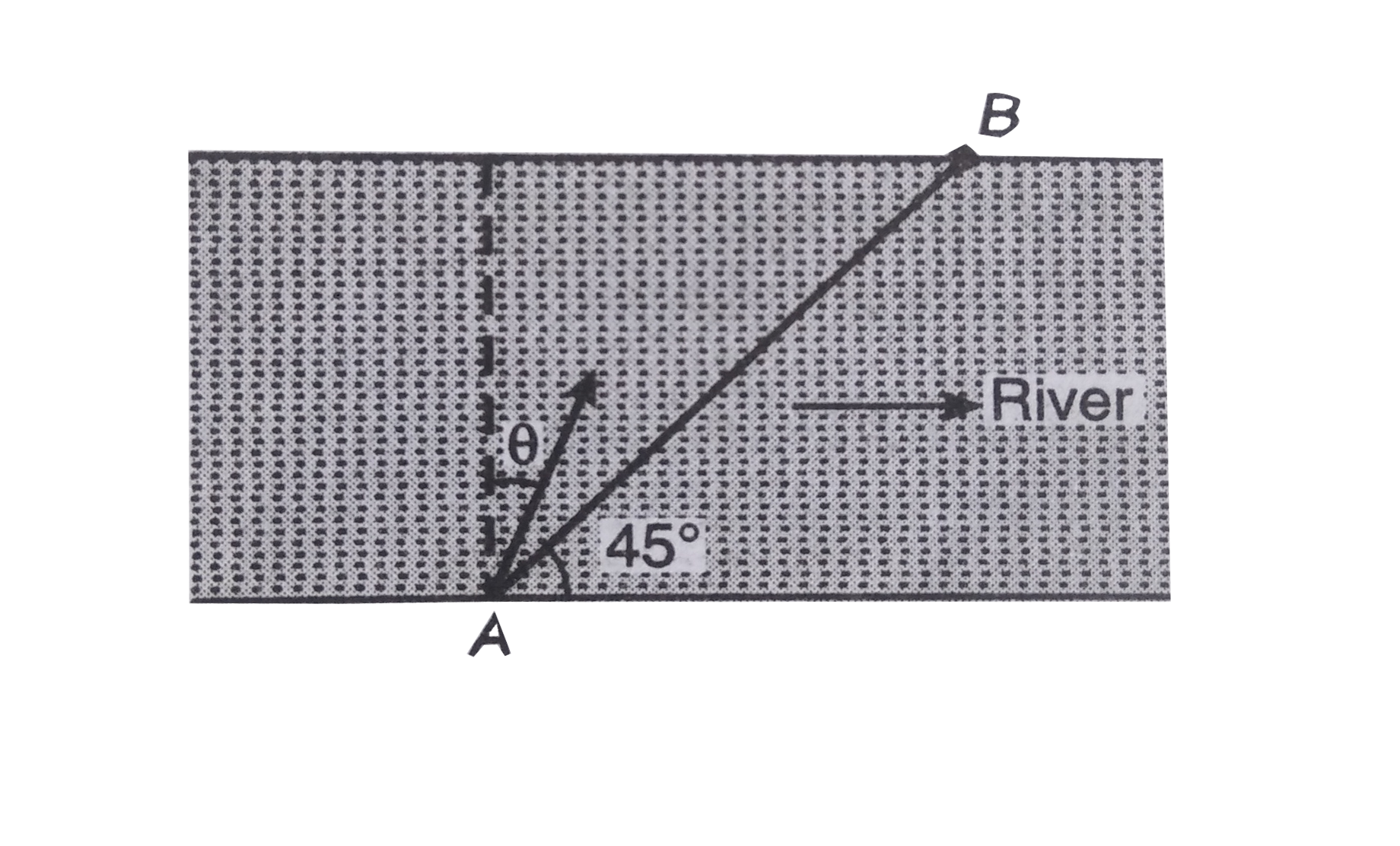
View SolutionGiven |Vbr|=4m/s= magnitude of velocity of boatman with respect to river, vr=2m/s in the directior shown. Boatman wants to reach from point A to point B. At what angle θ should he row his boat ?
View SolutionTwo boats A and B having same speed relative to river are moving in a river. Boat A moves normal to the river current as observed by an observer moving with velocity of river current. Boat B moves normal to the river as observed by the observer on the ground.
View Solution
