A bullet ofmass m is fired with a velocity 10m/s at angle θ with horizontal. At the hightest point of its trajectory, it collsides head-on with a bob of mass 3m suspended by a massless string of length 2/5m and gets embedded in the bob. After th collision the string moves through an angle of 60∘.
The horizontal coordinate of the intital position of the bob w.r.t. the point of firing of the bullet is n
95m
245m
94m
None of these
The correct Answer is:(B)
To solve the problem step by step, we will follow the outlined approach in the video transcript.
Step 1: Understand the Problem
We have a bullet of mass m fired at a velocity of 10m/s at an angle θ with the horizontal. At the highest point of its trajectory, it collides with a bob of mass 3m suspended by a massless string of length 25m. After the collision, the string makes an angle of 60∘ with the vertical. We need to find the horizontal coordinate of the initial position of the bob with respect to the point of firing of the bullet.
Step 2: Draw the Diagram
Draw a diagram showing the bullet's trajectory, the highest point of the bullet's path, and the bob hanging from the string. Mark the angle θ and the angle 60∘ after the collision.
Step 3: Find the Horizontal Distance at the Highest Point
At the highest point of its trajectory, the horizontal distance x from the firing point to the bob can be expressed in terms of the range R of the bullet:
x=R2
where R is the total range of the bullet.
Step 4: Calculate the Range of the Bullet
The range R of a projectile is given by:
R=u2sin(2θ)g
where u=10m/s and g=10m/s2.
Step 5: Use Conservation of Momentum for Collision
Before the collision, the momentum of the bullet is:
pinitial=m⋅(10cosθ)
After the collision, the total mass is 4m (bullet + bob), and they move together with speed v:
pfinal=4m⋅v
Using conservation of momentum:
m⋅(10cosθ)=4m⋅v
This simplifies to:
v=10cosθ4=5cosθ2
Step 6: Apply Conservation of Energy
The change in kinetic energy equals the change in potential energy:
ΔKE=ΔPE
At the highest point, the kinetic energy is:
KE=12⋅4m⋅v2
The potential energy change as the bob rises to height h is:
PE=4mgh
Setting these equal gives:
12⋅4m⋅v2=4mg⋅h
This simplifies to:
12v2=gh
Step 7: Determine Height h
The height h can be expressed in terms of the string length l and the angle 60∘:
h=l−lcos(60∘)=l(1−12)=l2
Substituting l=25:
h=12⋅25=15m
Step 8: Substitute h into Energy Equation
Substituting h into the energy equation:
12v2=g⋅15
Substituting g=10:
12v2=2⇒v2=4⇒v=2m/s
Step 9: Find cosθ and sinθ
Using the momentum equation:
v=5cosθ2⇒2=5cosθ2⇒cosθ=45
Using the Pythagorean identity:
sin2θ+cos2θ=1⇒sin2θ=1−(45)2=925⇒sinθ=35
Step 10: Calculate the Range R
Now we can calculate the range R:
R=u2sin(2θ)g=100⋅2⋅35⋅4510=100⋅242510=96m
Step 11: Find x
Finally, we find x:
x=R2=962=48m
Final Answer
The horizontal coordinate of the initial position of the bob with respect to the point of firing of the bullet is 48m.
---
We have a bullet of mass m fired at a velocity of 10m/s at an angle θ with the horizontal. At the highest point of its trajectory, it collides with a bob of mass 3m suspended by a massless string of length 25m. After the collision, the string makes an angle of 60∘ with the vertical. We need to find the horizontal coordinate of the initial position of the bob with respect to the point of firing of the bullet.
Draw a diagram showing the bullet's trajectory, the highest point of the bullet's path, and the bob hanging from the string. Mark the angle θ and the angle 60∘ after the collision.
At the highest point of its trajectory, the horizontal distance x from the firing point to the bob can be expressed in terms of the range R of the bullet:
x=R2
where R is the total range of the bullet.
The range R of a projectile is given by:
R=u2sin(2θ)g
where u=10m/s and g=10m/s2.
Before the collision, the momentum of the bullet is:
pinitial=m⋅(10cosθ)
After the collision, the total mass is 4m (bullet + bob), and they move together with speed v:
pfinal=4m⋅v
Using conservation of momentum:
m⋅(10cosθ)=4m⋅v
This simplifies to:
v=10cosθ4=5cosθ2
The change in kinetic energy equals the change in potential energy:
ΔKE=ΔPE
At the highest point, the kinetic energy is:
KE=12⋅4m⋅v2
The potential energy change as the bob rises to height h is:
PE=4mgh
Setting these equal gives:
12⋅4m⋅v2=4mg⋅h
This simplifies to:
12v2=gh
The height h can be expressed in terms of the string length l and the angle 60∘:
h=l−lcos(60∘)=l(1−12)=l2
Substituting l=25:
h=12⋅25=15m
Substituting h into the energy equation:
12v2=g⋅15
Substituting g=10:
12v2=2⇒v2=4⇒v=2m/s
Using the momentum equation:
v=5cosθ2⇒2=5cosθ2⇒cosθ=45
Using the Pythagorean identity:
sin2θ+cos2θ=1⇒sin2θ=1−(45)2=925⇒sinθ=35
Now we can calculate the range R:
R=u2sin(2θ)g=100⋅2⋅35⋅4510=100⋅242510=96m
Finally, we find x:
x=R2=962=48m
The horizontal coordinate of the initial position of the bob with respect to the point of firing of the bullet is 48m.
Topper's Solved these Questions
- BOOK - ALLENCHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-I40videos
CENTRE OF MASS
- BOOK - ALLENCHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-II43videos
CENTRE OF MASS
- BOOK - ALLENCHAPTER - BASIC MATHEMATICS USED IN PHYSICS &VECTORS EXERCISE - EXERCISE-IV ASSERTION & REASON11videos
BASIC MATHEMATICS USED IN PHYSICS &VECTORS
- BOOK - ALLENCHAPTER - ELASTICITY, SURFACE TENSION AND FLUID MECHANICSEXERCISE - Exercise 5 B (Integer Type Questions)3videos
ELASTICITY, SURFACE TENSION AND FLUID MECHANICS
Similar Questions
A bullet ofmass m is fired with a velocity 10m/s at angle θ with horizontal. At the hightest point of its trajectory, it collsides head-on with a bob of mass 3m suspended by a massless string of length 2/5m and gets embedded in the bob. After th collision the string moves through an angle of 60∘.
The angle θ isView SolutionA bullet ofmass m is fired with a velocity 10m/s at angle θ with horizontal. At the hightest point of its trajectory, it collsides head-on with a bob of mass 3m suspended by a massless string of length 2/5m and gets embedded in the bob. After th collision the string moves through an angle of 60∘.
The vertical coordinate of the initial positon of the bob w.r.t. the point of firing of the bullet isView SolutionA body of mass m is suspended by two strings making angles αandβ with the horizontal. Find the tensions in the strings.
View SolutionA bob of mass m suspended by a light inextensible string of length 'l' from a fixed point. The bob is given a speed of √6gl. Find the tension in the string when string deflects through an angle 120∘ from the vertical.
View SolutionA bob of mass m=50g is suspended form the ceiling of a trolley by a light inextensible string. If the trolley accelerates horizontally, the string makes an angle 37∘ with the vertical. Find the acceleration of the trolley.
 View Solution
View SolutionA bob of mass 1 kg is suspended from an inextensible string of length 1 m. When the string makes an angle 60∘ with vertical, speed of the bob is 4 m/s
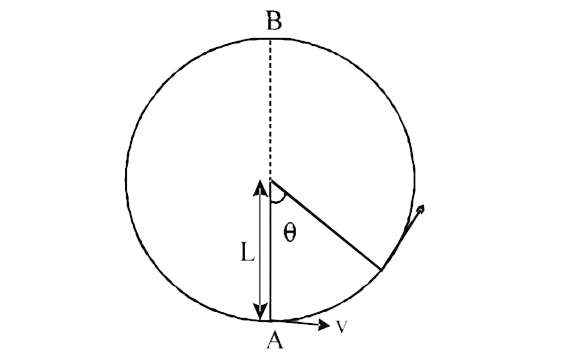
Upto what maximum height will the bob rise with respect to the bottommost point ?View SolutionA bob of mass M is suspended by a massless string of length L. The horizontal velocity v at position A is just sufficient to make it reach the point B. The angle θ at which the speed of the bob is half of that at A, satisfies
 View Solution
View SolutionA bob of mass 1 kg is suspended from an inextensible string of length 1 m. When the string makes an angle 60∘ with vertical, speed of the bob is 4 m/s
Net acceleration of the bob at this instant isView SolutionA simple pendulum with a bob of mass m is suspended from the roof of a car moving with horizontal acceleration a
View SolutionA bob of mass 10m is suspended through an inextensible string of length l. When the bob is at rest in equilibrium position, two particles, each of mass m, strike it as shown in Fig. The particles stick after collision. Choose the correct statement from the following:
 View Solution
View Solution

