The moment of inertia of a rod about an axis through its centre and perpendicular to it, is 112ML2 (where, M is the mass and L is length of the rod). The rod is bent in the middle, so that two halves make an angle of 60∘. The moment of inertia of the bent rod about the same axis would be
The correct Answer is:a
To find the moment of inertia of a bent rod about the same axis after bending it at an angle of 60∘, we can follow these steps:
Step 1: Understand the Initial Moment of Inertia
The moment of inertia I of a straight rod of mass M and length L about an axis through its center and perpendicular to it is given by:
I=112ML2
Step 2: Analyze the Bending of the Rod
When the rod is bent in the middle, it forms two halves, each with a mass of M2 and a length of L2. The two halves make an angle of 60∘ with respect to each other.
Step 3: Calculate the Moment of Inertia for Each Half
The moment of inertia of a rod about one of its ends is given by:
Iend=13mL2
For each half of the rod:
- Mass m=M2
- Length L=L2
Substituting these values into the formula:
I1=13(M2)(L2)2=13(M2)(L24)=ML224
Step 4: Calculate the Moment of Inertia for the Second Half
Since the second half of the rod is also identical to the first half, it will have the same moment of inertia:
I2=ML224
Step 5: Combine the Moments of Inertia
The total moment of inertia of the bent rod about the same axis is the sum of the moments of inertia of both halves:
Itotal=I1+I2=ML224+ML224=2ML224=ML212
Conclusion
Thus, the moment of inertia of the bent rod about the same axis remains:
I=ML212
The moment of inertia I of a straight rod of mass M and length L about an axis through its center and perpendicular to it is given by:
I=112ML2
When the rod is bent in the middle, it forms two halves, each with a mass of M2 and a length of L2. The two halves make an angle of 60∘ with respect to each other.
The moment of inertia of a rod about one of its ends is given by:
Iend=13mL2
For each half of the rod:
- Mass m=M2
- Length L=L2
I1=13(M2)(L2)2=13(M2)(L24)=ML224
Since the second half of the rod is also identical to the first half, it will have the same moment of inertia:
I2=ML224
The total moment of inertia of the bent rod about the same axis is the sum of the moments of inertia of both halves:
Itotal=I1+I2=ML224+ML224=2ML224=ML212
Thus, the moment of inertia of the bent rod about the same axis remains:
I=ML212
Topper's Solved these Questions
- ROTATIONAL MOTION BOOK - VMC MODULES ENGLISHCHAPTER - ROTATIONAL MOTION EXERCISE - LEVEL - 2 (Rotatinal Kinematics, Moment of Inertia)
10 Videos
- ROTATIONAL MOTION BOOK - VMC MODULES ENGLISHCHAPTER - ROTATIONAL MOTION EXERCISE - LEVEL - 2 (Torque, Fixed and Rotation)
10 Videos
- ROTATIONAL MOTION BOOK - VMC MODULES ENGLISHCHAPTER - ROTATIONAL MOTION EXERCISE - LEVEL - 1 (Mixed topics)
15 Videos
- REVISION TEST-2 JEEBOOK - VMC MODULES ENGLISHCHAPTER - REVISION TEST-2 JEEEXERCISE - PHYSICS
25 Videos
- SIMPLE HARMONIC MOTION BOOK - VMC MODULES ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - 7-previous year question
46 Videos
Similar Questions
The moment of inertia of a rod about an axis through its centre and perpendicular to it, is 112ML2 (where, M is the mass and L is length of the rod). The rod is bent in the middle, so that two halves make an angle of 45∘. The moment of inertia of the bent rod about the same axis would be
View SolutionCalculate the moment of inertia of the given rod about an axis CD

View SolutionCalculate the moment of inertia of the given rod about an axis CD.
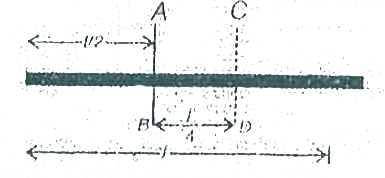
View SolutionThe moment of inertia of a thin uniform rod about an axis passing through its centre and perpendicular to its length is I0. What is the moment of inertia of the rod about an axis passing through one end and perpendicular to the rod ?
View SolutionA square frame is made rods each of mass m and length l. The moment of inertia of the square about its face diagonal is
View SolutionCalculate the moment of inertia of a rod of mass M, and length l about an axis perpendicular to it passing through one of its ends.
View SolutionA rod is placed along the line,y=2x with its centre at origin. The moment of inertia of the rod is maximum about.
View SolutionMoment of inertia of a thin rod of mass m and length l about an axis passing through a point l/4 from one end and perpendicular to the rod is
View SolutionThe moment of inertia of a uniform rod of length 2l and mass m about an axis xy passing through its centre and inclined at an enable α is

View SolutionA thin rod of length L of mass M is bent at the middle point O at an angle of 60∘. The moment of inertia of the rod about an axis passing through O and perpendicular to the plane of the rod will be

View Solution
