The moment of inertia of a rod about an axis through its centre and perpendicular to it, is 112ML2 (where, M is the mass and L is length of the rod). The rod is bent in the middle, so that two halves make an angle of 45∘. The moment of inertia of the bent rod about the same axis would be
148ML2
112ML2
124ML2
ML28√3
The correct Answer is:B
To solve the problem, we need to find the moment of inertia of a bent rod about an axis through its center and perpendicular to it after it has been bent at an angle of 45 degrees.
1. Understand the Initial Moment of Inertia:
The moment of inertia (I) of a straight rod about an axis through its center and perpendicular to its length is given by:
I=112ML2
where M is the mass of the rod and L is its length.
2. Bending the Rod:
When the rod is bent in the middle to form an angle of 45∘, it effectively creates two segments (each of length L2) that are at an angle to each other.
3. Calculate Moment of Inertia for Each Segment:
Each half of the rod has a mass of M2 and a length of L2. The moment of inertia of each half about its own center (which is at the midpoint of the half-rod) is:
Ihalf=112(M2)(L2)2=112⋅M2⋅L24=ML296
4. Use the Parallel Axis Theorem:
To find the moment of inertia about the original axis (the axis through the center of the entire rod), we need to apply the parallel axis theorem. The distance from the center of each half-rod to the axis is L4 (since the center of the bent rod is at the midpoint of the original rod).
The moment of inertia of each half-rod about the original axis is given by:
Itotal=Ihalf+M2(L4)2
where M2 is the mass of each half-rod and (L4)2 is the square of the distance from the center of the half-rod to the original axis.
Substituting the values:
Itotal=ML296+M2⋅L216
Simplifying the second term:
M2⋅L216=ML232
5. Combine the Moments of Inertia:
Now, we need to combine both contributions:
Itotal=ML296+ML232
To add these fractions, we need a common denominator, which is 96:
ML232=3ML296
Therefore:
Itotal=ML296+3ML296=4ML296=ML224
6. Final Result:
The moment of inertia of the bent rod about the same axis is:
I=ML224
The moment of inertia (I) of a straight rod about an axis through its center and perpendicular to its length is given by:
I=112ML2
where M is the mass of the rod and L is its length.
When the rod is bent in the middle to form an angle of 45∘, it effectively creates two segments (each of length L2) that are at an angle to each other.
Each half of the rod has a mass of M2 and a length of L2. The moment of inertia of each half about its own center (which is at the midpoint of the half-rod) is:
Ihalf=112(M2)(L2)2=112⋅M2⋅L24=ML296
To find the moment of inertia about the original axis (the axis through the center of the entire rod), we need to apply the parallel axis theorem. The distance from the center of each half-rod to the axis is L4 (since the center of the bent rod is at the midpoint of the original rod).
Itotal=Ihalf+M2(L4)2
where M2 is the mass of each half-rod and (L4)2 is the square of the distance from the center of the half-rod to the original axis.
Itotal=ML296+M2⋅L216
Simplifying the second term:
M2⋅L216=ML232
Now, we need to combine both contributions:
Itotal=ML296+ML232
To add these fractions, we need a common denominator, which is 96:
ML232=3ML296
Therefore:
Itotal=ML296+3ML296=4ML296=ML224
The moment of inertia of the bent rod about the same axis is:
I=ML224
Similar Questions
The moment of inertia of a rod about an axis through its centre and perpendicular to it, is 112ML2 (where, M is the mass and L is length of the rod). The rod is bent in the middle, so that two halves make an angle of 60∘. The moment of inertia of the bent rod about the same axis would be
View SolutionCalculate the moment of inertia of the given rod about an axis CD

View SolutionCalculate the moment of inertia of the given rod about an axis CD.
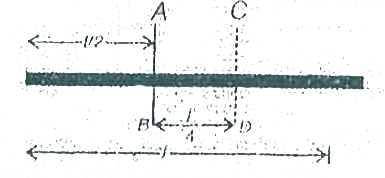
View SolutionThe moment of inertia of a thin uniform rod about an axis passing through its centre and perpendicular to its length is I0. What is the moment of inertia of the rod about an axis passing through one end and perpendicular to the rod ?
View SolutionA square frame is made rods each of mass m and length l. The moment of inertia of the square about its face diagonal is
View SolutionCalculate the moment of inertia of a rod of mass M, and length l about an axis perpendicular to it passing through one of its ends.
View SolutionA rod is placed along the line,y=2x with its centre at origin. The moment of inertia of the rod is maximum about.
View SolutionMoment of inertia of a thin rod of mass m and length l about an axis passing through a point l/4 from one end and perpendicular to the rod is
View SolutionThe moment of inertia of a uniform rod of length 2l and mass m about an axis xy passing through its centre and inclined at an enable α is

View SolutionMoment of inertia of a uniform rod of length L and mass M, about an axis passing through L/4 from one end and perpendicular to its length is
View Solution
