a particle is moving in x-y-plane at 2m/s along x-axis. 2 seconds later, its velocity is 4m/s in a direction making 60∘ with positive x-axis. Its average acceleration for the period of motion is:-
√5m/s2, along y-axis
√3m/s2, along y-axis
√5m/s2, along at 60∘ with positive x-axis
3m/s2 at 60∘ with positive x-axis.
The correct Answer is:B
To solve the problem, we will follow these steps:
Step 1: Identify the initial and final velocities
- The initial velocity Vi is given as 2m/s along the x-axis. In vector form, this can be represented as:
Vi=2^i
- The final velocity Vf is given as 4m/s at an angle of 60∘ with the positive x-axis. We can break this into its x and y components:
Vfx=4cos(60∘)=4×12=2m/s
Vfy=4sin(60∘)=4×√32=2√3m/s
Thus, the final velocity in vector form is:
Vf=2^i+2√3^j
Step 2: Calculate the change in velocity
The change in velocity ΔV is given by:
ΔV=Vf−Vi
Substituting the values:
ΔV=(2^i+2√3^j)−(2^i)=2√3^j
Step 3: Calculate the average acceleration
The average acceleration aavg is given by the change in velocity divided by the time interval. The time interval is 2s:
aavg=ΔVΔt=2√3^j2=√3^jm/s2
Step 4: Final Result
Thus, the average acceleration of the particle is:
aavg=√3^jm/s2
- The initial velocity Vi is given as 2m/s along the x-axis. In vector form, this can be represented as:
Vi=2^i
Vfx=4cos(60∘)=4×12=2m/s
Vfy=4sin(60∘)=4×√32=2√3m/s
Thus, the final velocity in vector form is:
Vf=2^i+2√3^j
The change in velocity ΔV is given by:
ΔV=Vf−Vi
Substituting the values:
ΔV=(2^i+2√3^j)−(2^i)=2√3^j
The average acceleration aavg is given by the change in velocity divided by the time interval. The time interval is 2s:
aavg=ΔVΔt=2√3^j2=√3^jm/s2
Thus, the average acceleration of the particle is:
aavg=√3^jm/s2
Topper's Solved these Questions
- BOOK - ALLENCHAPTER - KINEMATICSEXERCISE - EXERCISE-0257videos
KINEMATICS
- BOOK - ALLENCHAPTER - KINEMATICSEXERCISE - EXERCISE-036videos
KINEMATICS
- BOOK - ALLENCHAPTER - KINEMATICSEXERCISE - EXERCISE-289videos
KINEMATICS
- BOOK - ALLENCHAPTER - ERROR AND MEASUREMENTEXERCISE - Part-2(Exercise-2)(B)22videos
ERROR AND MEASUREMENT
- BOOK - ALLENCHAPTER - KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)EXERCISE - BEGINNER S BOX-78videos
KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)
Similar Questions
Displacement-time curve of a particle moving along a straight line is shown. Tangents at A and B makes angle 45∘ and 135∘ with positive x-axis respectively. The average acceleration of the particle during t=1,t=2 seconds is
 View Solution
View SolutionA particle moves in the x-y plane with a constant acceleration of 1.5m/s2 in the direction making an angle of 37∘ with the x-axis.
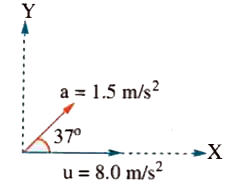
At t=0 the particle is at the origin and its velocity is 8.0m/s along the x- aixs . Find the velocity and the position of the particle at t = 4.0s.View SolutionA positively charged particle moving along x-axis with a certain velocity enters a uniform electric field directed along positive y-axis. Its
View SolutionA particle is moving along a straight line along x-zxis with an initial velocity of 2m/s towards positive x-axis. A constant acceleration of 0.5m/s2 towards negative x-axis starts acting on particle at t=0. Find velocity (in m/s) of particle at t=2s.
View SolutionA particle is moving along x-axis such that its velocity varies with time according to v=(3m/s2)t−(2m/s3)t2. Find the velocity at t = 1 s and average velocity of the particle for the interval t = 0 to t = 5 s.
View SolutionA particle is moving along x-y plane. Its x and y co-ordinates very with time as x=2t2andy=t3 Here, x abd y are in metres and t in seconds. Find average acceleration between a time interval from t=0 to t=2s.
View SolutionA particle had a speed of 18 m/s at a certain time, and 2.5 s later its speed was 30 m/s in the opposite direction. The average acceleration of the particle in the duration is :
View SolutionThe v-t graph for a particle moving along x-axis is shown in the figure, find
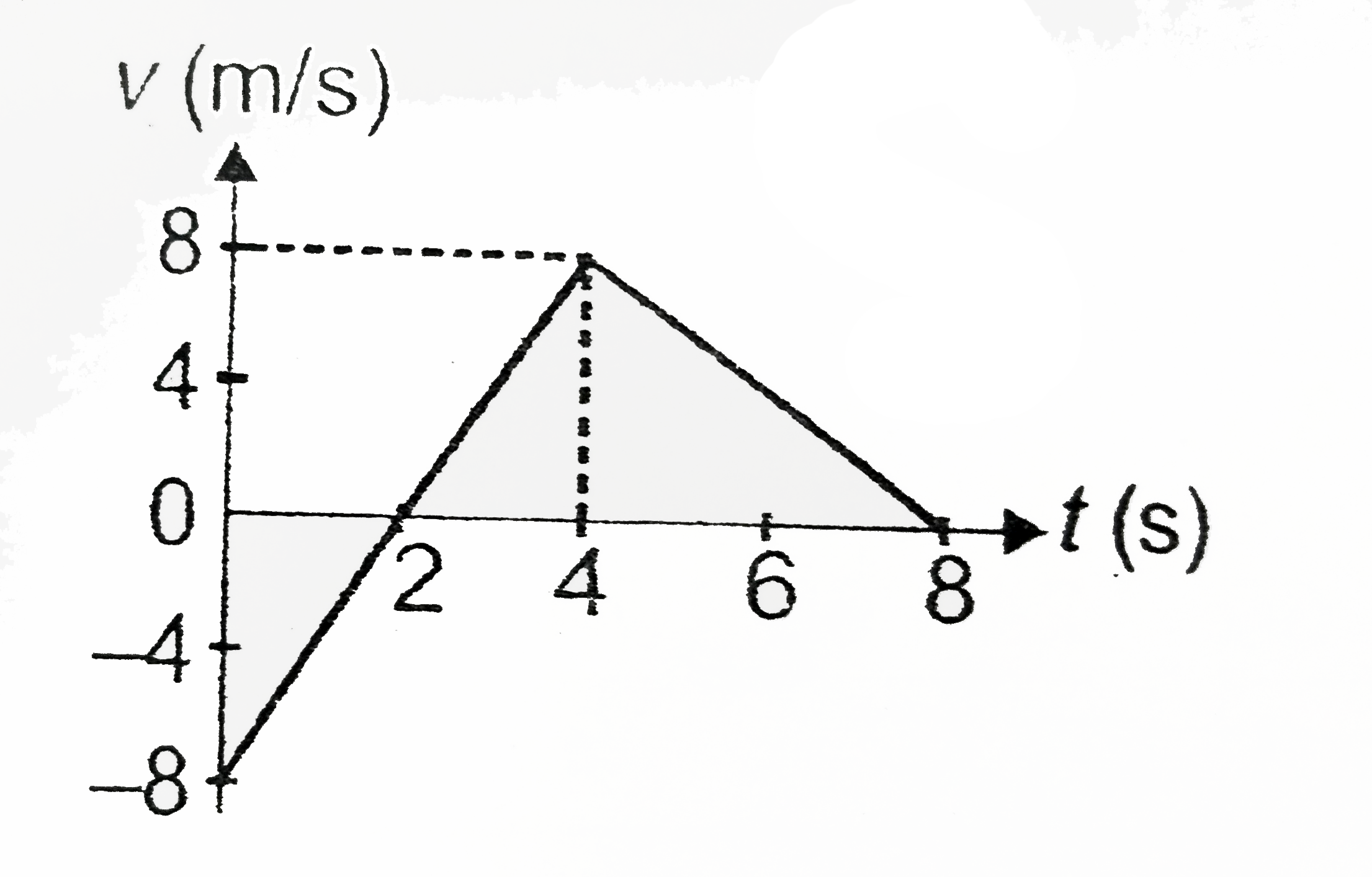
(a) Average velocity in the interval 0 to 8 s.
(b) Average speed in the interval 0 to 8 s.
(c) Average acceleration in the interval 0 to 4 s.
(d) Instantaneous acceleration at t = 2.5 s.View SolutionA particle movesin the X-Y plane with a constasnt acceleration of 1.5ms2 in the direction making an angle of 370 with the X-axis.At t=0 the particle is at the orign and its velocity is 8.0 m/s along the X-axis. Find the velocity and the position of the particle at t=4.0 s.
 View Solution
View SolutionTwo particles are moving along x-axis. Particle-1 starts from x=−10m with velocity 4m/s along negative x-direction and acceleration 2m/s2 along positive x-direction. Particle-2 starts from x=+2m with velocity 6m/s along positive x-direction and acceleration 2m/s2 along negative x-direction.
(a) Find the time when they collide.
(b) Find the x-coordinates where they collide. Both start simultaneously.View Solution

