The friction coefficient between the board and the floor shown in figure is μ Find the maximum force that the man can exert on the rope so that the board does not slip on the floor

N+T=(N+m)g
N=(M+m)g−T
Condition of man for no slipping to be occur is
T=fr⇒T=μN⇒T=μ(M+m)g−T)
⇒T(1+μ)=μ(M+m)g⇒T=μ(M+m)g(1+μ)
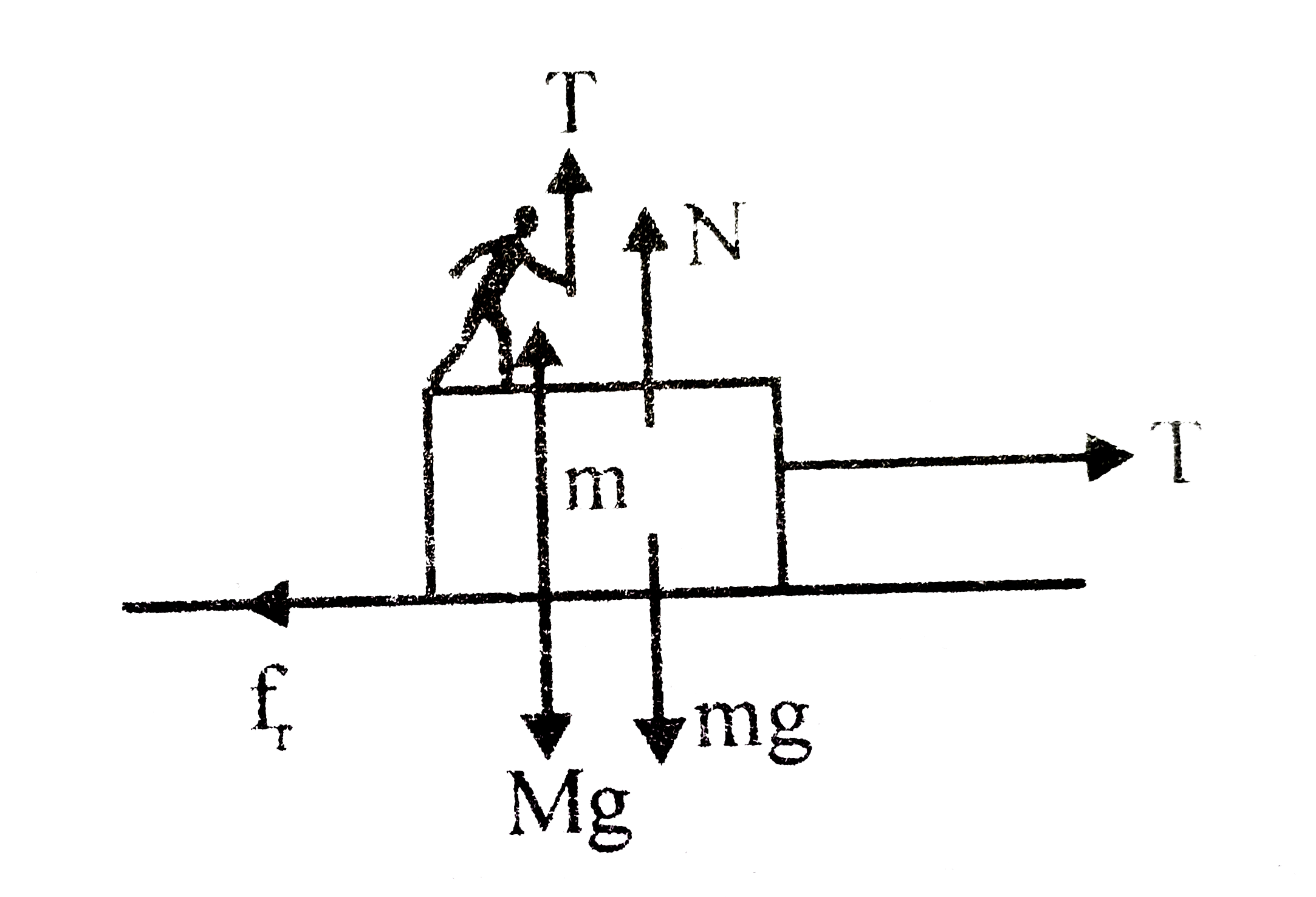
Topper's Solved these Questions
- BOOK - ALLENCHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - EXERCISE-I52videos
NEWTONS LAWS OF MOTION
- BOOK - ALLENCHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - EXERCISE-II112videos
NEWTONS LAWS OF MOTION
- BOOK - ALLENCHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - EXERCISE-III28videos
NEWTONS LAWS OF MOTION
- BOOK - ALLENCHAPTER - NEWTON'S LAWS OF MOTION & FRICTIONEXERCISE - EXERCISE (JA)4videos
NEWTON'S LAWS OF MOTION & FRICTION
- BOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (Wave Motion & Dopplers Effect) (Stationary waves & doppler effect, beats)24videos
RACE
Similar Questions
The friction coeficient bettween the board and the floor shownin filgure is μ. Find the maximum force that the man can exert on the rope so tht the board does not slipon the floor.
 View Solution
View SolutionThe friction coefficient between the board and the floor shown in figure is μ Find the maximum force that the man can exert on the rope so that the board does not slip on the floor
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A block of mass m=2kg is resting on a rough inclined plane of inclination of 30∘ as shown in figure. The coefficient of friction between the block and the plane is μ=0.5. What minimum force F should be applied perpendicular to the plane on the block, so that blocks does not slip on the plane? (g=10m/s2)
 A2.68 NBZeroC4.34 ND6.24 N
A2.68 NBZeroC4.34 ND6.24 N
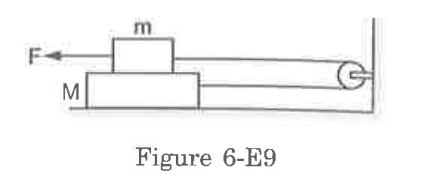
The friction coefficient between plank and floor is μ. The man applies, the maximum possible force on the string and the system remains at rest. Then
 View Solution
View SolutionThe coefficient of static friction between a block of mass m and an incline is μs=0.3, a. What can be the maximum angle θ of the incline with the horizontal so that the block does not slip on the plane? b. If the incline makes an angle θ2 with the horizontal, find the frictional force on the block.
View SolutionIf the coefficient of friction between the wedge A and block B shown in the figure is μ, then the maximum possible horizontal acceleration of A for which B doesn’t slip is [ angle of inclination of wedge = 45∘ ]
 View Solution
View SolutionA block of mass m=2kg is resting on a inclined plane of inclination 30∘ as shown in figure The coefficient of friction between the block and the plane is μ=0.5 what minimum force F (in newton) should be applied perpendicular to the plane on the block so that the does not slip on the plane?
 View Solution
View SolutionThe friction coefficient between the two blocks shown in figure is μ but the floor is smooth. A. What maximum horizontal force F can be applied without disturbing the equilibrium of the systme? b.suppose the horizontal force applied is double of that found in part a. Findthe accelerations of the two masses.
 View Solution
View SolutionA bar of mass m is placed on a triangular block of mass M as shown in figure The friction coefficient between the two surface is μ and ground is smooth find the minimum and maximum horizontal force F required to be applied on block so that the bar will not slip on the inclined surface of block
 View Solution
View SolutionThe friction coefficient between the two blocks shown in figure is μ and the horizontal plane is smooth. A. If the system is slightly diplaced and released find the time period. B. find the magnitude of the frictional force between the blocks when the displacement from the mean position is x. c. What can be the maximum amplitude if the upper block does not slip relative to the lower block?
 View Solution
View Solution

