The focal length of a concave mirror is 30cm.Find the position of the object in front of the mirror,so that the image is three times the size of the objects.
To solve the problem, we need to find the position of the object in front of a concave mirror such that the image formed is three times the size of the object. Given the focal length of the concave mirror is 30 cm, we can follow these steps:
Step 1: Understand the Magnification Formula
The magnification (m) of a mirror is given by the formula:
m=−vu
where:
- v = distance of the image from the mirror
- u = distance of the object from the mirror
Since the image is three times the size of the object, we have:
m=3
Step 2: Relate Image Distance to Object Distance
From the magnification formula, we can express the image distance v in terms of the object distance u:
m=−vu
Substituting m=3:
3=−vu
This gives us:
v=−3u
Step 3: Use the Mirror Formula
The mirror formula for concave mirrors is given by:
1f=1v+1u
where f is the focal length of the mirror. Given f=−30 cm (negative for concave mirrors), we can substitute the values:
1−30=1−3u+1u
Step 4: Simplify the Equation
Now, we need to simplify the equation:
1−30=−13u+1u
To combine the fractions on the right side, find a common denominator:
1−30=−13u+33u
This simplifies to:
1−30=23u
Step 5: Cross-Multiply to Solve for u
Cross-multiplying gives:
2⋅(−30)=3u
−60=3u
Now, divide both sides by 3:
u=−20 cm
Step 6: Interpret the Result
The negative sign indicates that the object is placed in front of the mirror, which is consistent with the convention for concave mirrors. Thus, the object should be placed at a distance of 20 cm from the mirror.
Final Answer
The position of the object in front of the concave mirror should be at 20 cm.
---
The magnification (m) of a mirror is given by the formula:
m=−vu
where:
- v = distance of the image from the mirror
- u = distance of the object from the mirror
m=3
From the magnification formula, we can express the image distance v in terms of the object distance u:
m=−vu
Substituting m=3:
3=−vu
This gives us:
v=−3u
The mirror formula for concave mirrors is given by:
1f=1v+1u
where f is the focal length of the mirror. Given f=−30 cm (negative for concave mirrors), we can substitute the values:
1−30=1−3u+1u
Now, we need to simplify the equation:
1−30=−13u+1u
To combine the fractions on the right side, find a common denominator:
1−30=−13u+33u
This simplifies to:
1−30=23u
Cross-multiplying gives:
2⋅(−30)=3u
−60=3u
Now, divide both sides by 3:
u=−20 cm
The negative sign indicates that the object is placed in front of the mirror, which is consistent with the convention for concave mirrors. Thus, the object should be placed at a distance of 20 cm from the mirror.
The position of the object in front of the concave mirror should be at 20 cm.
Topper's Solved these Questions
- GEOMETRICAL OPTICSBOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - SOME WORKED OUT EXAMPLES
83 Videos
- GEOMETRICAL OPTICSBOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - EXERCISE -01
65 Videos
- CURRENT ELECTRICITYBOOK - ALLENCHAPTER - CURRENT ELECTRICITYEXERCISE - EX.II
66 Videos
- GRAVITATIONBOOK - ALLENCHAPTER - GRAVITATIONEXERCISE - EXERCISE 4
9 Videos
Similar Questions
Find the distance of object from a concave mirror of focal length 10 cm so that image size is four time the size of the object.
View SolutionThe image produced by a concave mirror is one-quarter the size of object. If the object is moved 5cm closer to the mirror, the image will only be half the size of the object. The focal length of mirror is
View SolutionFind the distance of object form a concave morror of focal length 10 cm so that image size is four times the size of the object.
View SolutionThe focal length of a concave mirror is 50cm. Where an object be placed so that its image is two times and inverted
View SolutionA concave mirror has a focal length of 20 cm. Find the position or positions of an object for which the image-size is double of the object-size.
View SolutionThe image formed by a concave mirror is twice the size of the object. The focal length of the mirror is 20 cm. The distance of the object from the mirror is/are
View SolutionA concave mirror forms a real image of an object placed in front of it at a distance 30 cm, of size three times the size of object. Find position of image.
View SolutionObject AB is placed on the axis of a concave mirror of focal length 10cm. End A of the object is at 30cm from the mirror. Find the length of the image
a. if length of object is 5cm.
b. if length of object is 1 mm.
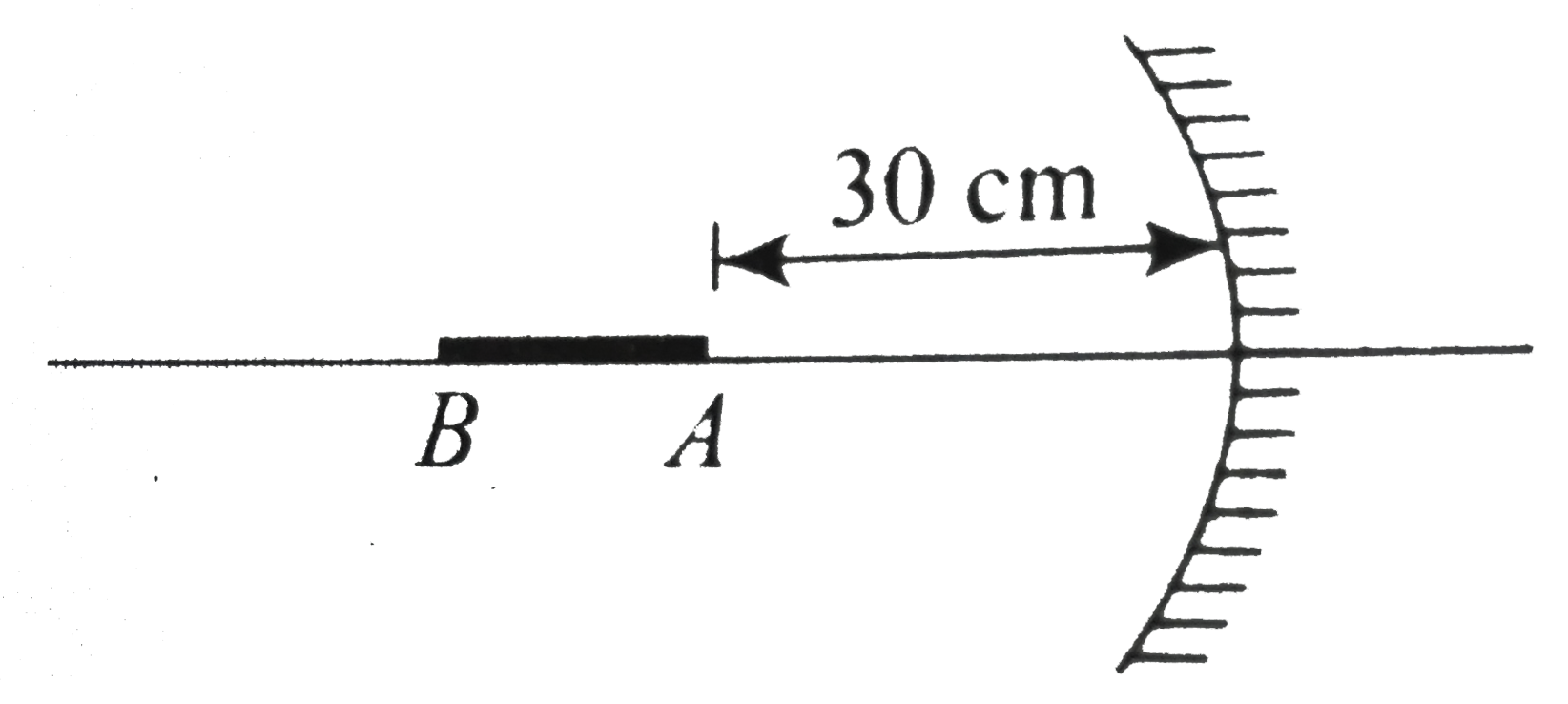
View SolutionA concave mirror has a focal length 20 cm. The distance between the two positions of the object for which the image size is double of the object size is
View SolutionFor what position of an object, a concave mirror forms a real image equal in size to the object?
View Solution
