Two non - viscous, incompressible and immiscible liquids of densities (rho) and (1.5 rho) are poured into the two limbs of a circular tube of radius ( R) and small cross section kept fixed in a vertical plane as shown in fig. Each liquid occupies one fourth the cirumference of the tube.
Find the angle (theta) that the radius to the interface makes with the verticles in equilibrium position.
The correct Answer is:A, B, C
(a) Let the liqud of density 1.5ρ occupy the lect portion AB and the liquid of density ρoccupy the right portion BC of the tube. The pressure at the lowest point D due to the liquid on the left is
P1=(R−Rsinθ)1.5ρg
_E01_113_S01.png)
The pressure due to the liquid on the right is
P2(Rsinθ+Rcosθ)ρg+(R−Rcosθ)1.5ρg
Since the liquids ar in equilibrium
P1=P2 or (R−Rsinθ)1.5ρg=(R−Rcosθ)ρg+(R−Rcosθ)1.5ρg
Solving, we get
tanθ=0.2 or θ=tan−1(0.2)
(b) Let the whole liquid lbe given a small angular displacement α towards right. Then the pressure difference between the right and the left limbs is
dP=P2−P1
=[Rsin(θ+α)+Rcos(θ+α)ρg+[R−Rcos(θ+α)1.5ρg−[R−Rsin(θ+α)]1.5ρg
=Rρg[2.5sin(θ+α)−0.5cos(θ+α)]
=Rρg[2.5(sinθcosα+cosθsinα)−0.5(cosθcosα−sinθsinα)]
For small α
sinα=α,cosα≅1∴dP=Rρg
[2.5sinθ+2.5αcosθ−0.5cosθ+0.5αsinθ]
As tanθ=0.2,sinθ0.2√1.04≈0.2,cosθ=1√1.04≈1
∴dP=Rρg[2.5×0.2+2.5α−0.5+0.5×0.2α]
=Rρg[2.6α]
=236ρg
where y=Rα, the linear displacement
∴ Restoring force F=2.6ρgAy
This shows that F∝y
Hence the motion is simple harmonic with force constant
k=2.6ρgA
Now, total mass of the liquid
m=2πR4Aρ+2πR4A(1.5p)=5πRAρ4
∴ Time period
T=2π√mk=2π√5πrAρ4×236ρgA=π√1.93πR9.8
=2.47√R seconds.
Topper's Solved these Questions
- BOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercise-05 [A]39videos
SIMPLE HARMONIC MOTION
- BOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercise-05 [B]12videos
SIMPLE HARMONIC MOTION
- BOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercise-04 [A]20videos
SIMPLE HARMONIC MOTION
- BOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (Wave Motion & Dopplers Effect) (Stationary waves & doppler effect, beats)24videos
RACE
- BOOK - ALLENCHAPTER - TEST PAPEREXERCISE - PHYSICS4videos
TEST PAPER
Similar Questions
A small uniform tube is bent into a circle of radius r whose plane is vertical. Equal volumes of two fluids whose densities areρ and σ(ρ>σ) fill half the circle. Find the angle that the radius passing through the interface makes with the vertical.
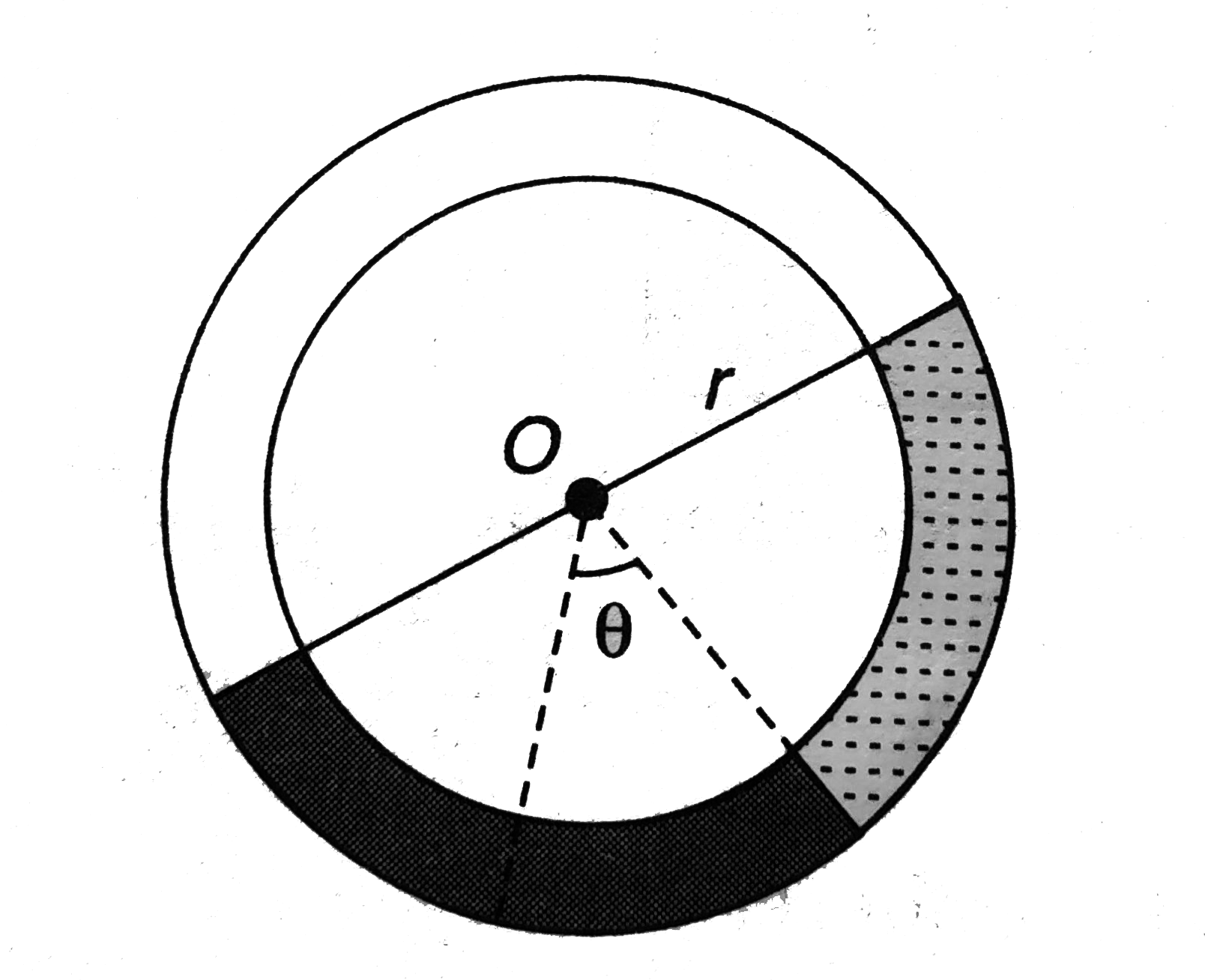 View Solution
View SolutionA V-shaped glass tube of uniform cross section is kept in a vertical plane as shown. A liquid is poured in the tube. In equilibrum the level of liquid in both limds of tube. Find the angular frequency of small oscillation of liquid.
 View Solution
View SolutionA wooden plank of length 1m and uniform cross-section is hinged at one end to the bottom of a tank as shown in fig. The tank is filled with water upto a hight 0.5m. The specific gravity of the plank is 0.5. Find the angle θ that the plank makes with the vertical in the equilibrium position. (Exclude the case θ=θ∘)
 View Solution
View SolutionA circular tube of uniform cross section is filled with two liquids densities ρ1 and ρ2 such that half of each liquid occupies a quarter to volume of the tube. If the line joining the free surfaces of the liquid makes an angle θ with horizontal find the value of θ.
 View Solution
View SolutionThe wooden plank of length 1 m and uniform cross section is hinged at one end to the bottom of a tank as shown in figure. The tank is filled with water up to a height of 0.5 m. The specific gravity of the plank is 0.5. Find the angle θ that the plank makes with the vertical in the equilibrium position. (Exclude the case θ=0)
 ,View Solution
,View SolutionA uniform long tube is bent into a circle of radius R and it lies in vertical plane. Two liquids of same volume but densities ρ and δ fill half the tube. The angle θ is
 View Solution
View SolutionThere is a circular tube in a vertical plane. Two liquids which do not mix and of densities d1andd2 are filled in the tube. Each liquid subtends 90∘ angle at centre. Radius joining their interface make an angle α with vertical. Ratio d1d2 is :
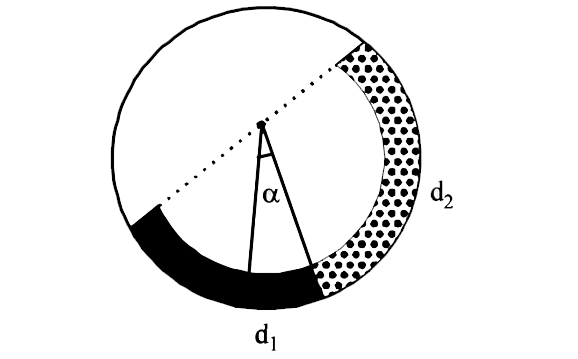 View Solution
View SolutionA tube in vertical plane is shown in figure. It is filled with a liquid of density ρ and its end B is closed. Then the force exerted by the fluid on the tube at end B will be: [Assume the radius of the tube to be negligible in comparison to l]
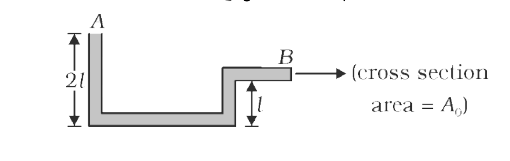 View Solution
View SolutionIn a U-tube, two immiscible liquids of density ρ1andρ2 are arranged as shown in figure. The right part of the tube is closed at the top and some air is entrapped above liquid of density ρ2. The gauge pressure of this air is :
 View Solution
View SolutionA liquid of density ρ is filled in a U-tube is accelerated with an acceleration a so that the height of liquid in its two vertical arms are h1andh2 as shown in the figure. If l is the length of horizontal arm of the tube, the acceleration a is
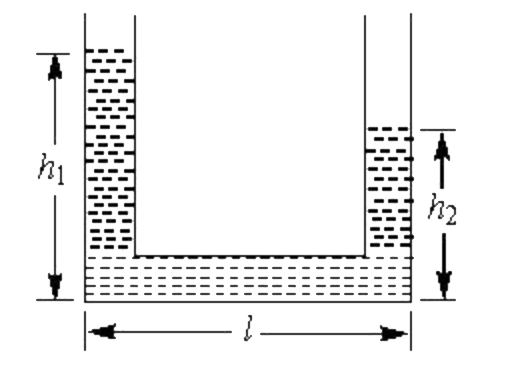 View Solution
View Solution

