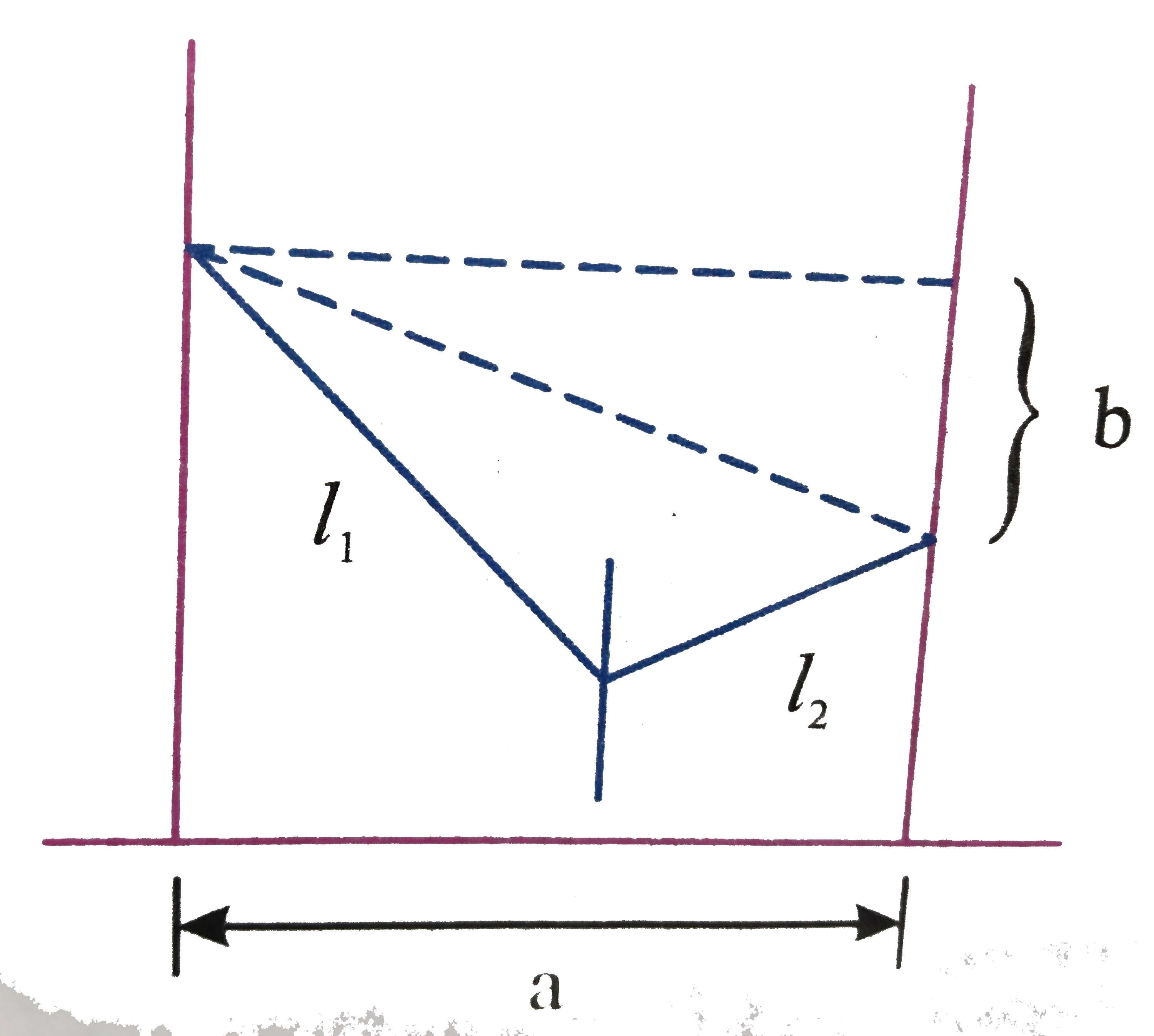
Consider a swing whose one end is fixed above the other rope by ''b'. The distance between the poles of swing is a. The lengths l1 and l2 are such that l21+l22=a2+b2 as shown. The period of the smaller oscillations of the swing, by neglecting the height of the swinging person, is.....
The correct Answer is:A, B
Given a2+b2=l21+l22
tanθ=ba
tanα=l2l1
Let OT=x1,TQ=x1,PT=dTS=y
From geometry
d+y=l1sin(α+β)
and d+l1cos(α+θ)tanθ=l1sin(α+θ)
⇒d=l1l2a∴T=2π√dg=2π√l1l2ag
_E01_115_S01.png)
Topper's Solved these Questions
- BOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercise-05 [A]39videos
SIMPLE HARMONIC MOTION
- BOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercise-05 [B]12videos
SIMPLE HARMONIC MOTION
- BOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercise-04 [A]20videos
SIMPLE HARMONIC MOTION
- BOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (Wave Motion & Dopplers Effect) (Stationary waves & doppler effect, beats)24videos
RACE
- BOOK - ALLENCHAPTER - TEST PAPEREXERCISE - PHYSICS4videos
TEST PAPER
Similar Questions
A spring whose instretched length is l has a force constant k. The spring is cut into two pieces of unstretched lengths l1 and l2 where, l1=nl2 and n is an integer. The ratio k1/k2 of the corresponding force constant, k1 and k2 will be :
View SolutionFind the shortest distance between the lines l1andl2 given by
x−1−1=y3=z−22andx2=y−1−6=z−4View SolutionA uniform spring whose unstretched length is l has a force constant k. the spring is cut into two pieces of unstretched lengths l1 and l2, where l1=nl2 and n is an integer. What are the corresponding force constant k1 and k2 in terms of n and k?
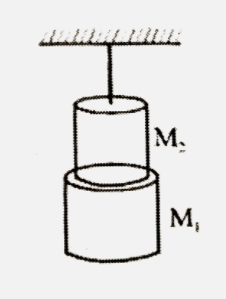
View SolutionThe length of wire, when M1 is hung from it, is l1 and is l2 with both M1 and M2 hanging. The natural length of wire is :-
 View Solution
View SolutionOne end of thermally insulated rod is kept at a temperature T1 and the other at T2. The rod is composed of two section of length l1 and l2 thermal conductivities k1 and k2 respectively. The temerature at the interface of two section is
View SolutionOne end of thermally insulated rod is kept at a temperature T1 and the other at T2. The rod is composed of two section of length l1 and l2 thermal conductivities k1 and k2 respectively. The temerature at the interface of two section is
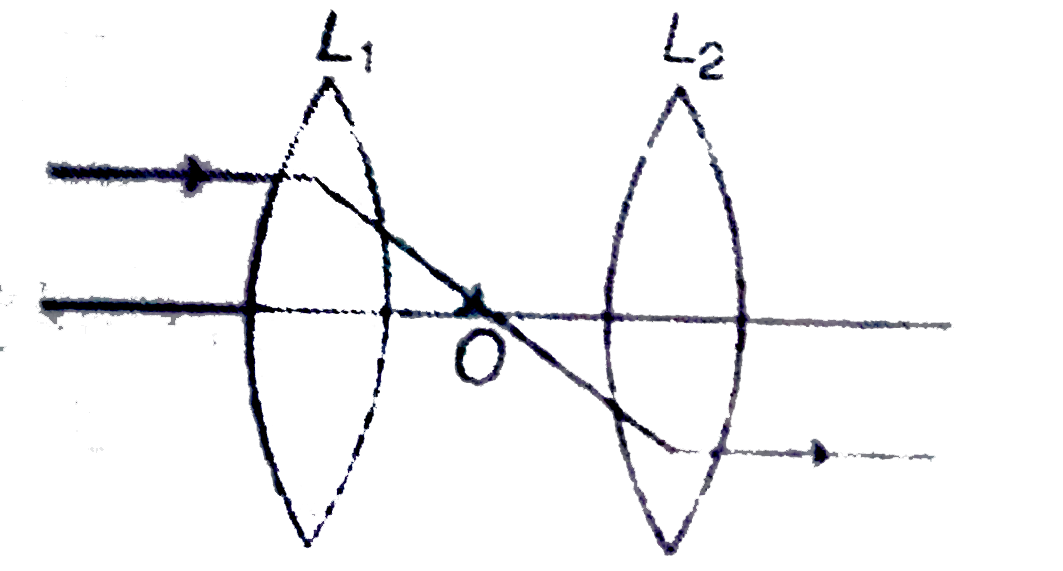
View SolutionIn the figure shown, there are two convex lenses L1 and L2 having focal. Lengths f1 and f2 respectively. The distance between L1 and L2 will be
 View Solution
View SolutionIf l1,l2,l3 are respectively the perpendicular from the vertices of a triangle on the opposite side, then show that l1l2l3=a2b2c28R3.
View SolutionTwo simple pendulum first of bob mass M1 and length L1 second of bob mass M2 and length L2M1=M2 and L1 = 2L_(2). if the vibrational energy of both is same which is correct?
View SolutionTwo simple pendulum first of bob mass M1 and length L1 second of bob mass M2 and length L2M1=M2 and L1 = 2L_(2). if the vibrational energy of both is same which is correct?
View Solution

