A particle of mass (m) is attached to a spring (of spring constant k) and has a natural angular frequency ω0. An external force F(t) proportional to cosωt (ω≠ω0) is applied to the oscillator. The time displacement of the oscillator will be proportional to.
mω20−ω2
1m(ω20−ω2)
1m(ω20+ω2)
mω20+ω2
The correct Answer is:B
Natural frequency of oscillator =ω0
Frequency of the applied force =ω
Net force acting on oscillator at a displacement x
=m(ω02−ω2)x…..(i)
From eqs. (i) and (ii) we get
m(ω02−ω2)x∝cosωt.......(ii)
Also x=Acosωt.....(vi)
From eqs. (iii) and (iv), we get
m(ω02−ω2)Acosωt∝cosωt⇒A∝1m(ω20−ω2)
Topper's Solved these Questions
- BOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercise-05 [B]12videos
SIMPLE HARMONIC MOTION
- BOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - MCQ s one or more than one correct answers5videos
SIMPLE HARMONIC MOTION
- BOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercise-04 [B]105videos
SIMPLE HARMONIC MOTION
- BOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (Wave Motion & Dopplers Effect) (Stationary waves & doppler effect, beats)24videos
RACE
- BOOK - ALLENCHAPTER - TEST PAPEREXERCISE - PHYSICS4videos
TEST PAPER
Similar Questions
A particle of mass m is fixed to one end of a massless spring of spring constant k and natural length l0. The system is rotated about the other end of the spring with an angular velocity ω ub gravity-free space. The final length of spring is
View SolutionA uniform disc of mass m is attached to a spring of spring constant k as shown in figure and there is sufficient friction to prevent slipping of disc. Time period of small oscillations of disc is:
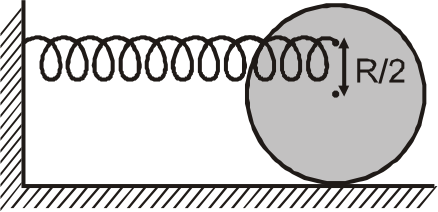 View Solution
View SolutionA body of mass 4 kg is made to oscillate on a spring of force constant 10 N/m. Calculate (i) angular frequency (2) frequency of vibration and (3) time period of vibration.
View SolutionWhen a particle of mass m is attached to a vertical spring of spring constant k and released, its motion is described by y(t)=y0sin2ωt, where 'y' is measured from the lower end of unstretched spring. Then ω is :
View SolutionA constant force(F) is applied on a stationary particle of mass 'm'. The velocity attained by the particle in a certain displacement will be proportional to
View SolutionA constant force (F) is applied on a stationary particle of mass m, the velocity attained by the particle in a certain interval of time will be proportional to
View SolutionA particles of mass m is fixed to one end of a light spring of force constant k and unstreatched length l. the system is rotated about the other end of the spring with an angular velocity ω in gravity free space. The increase in length of the spring is
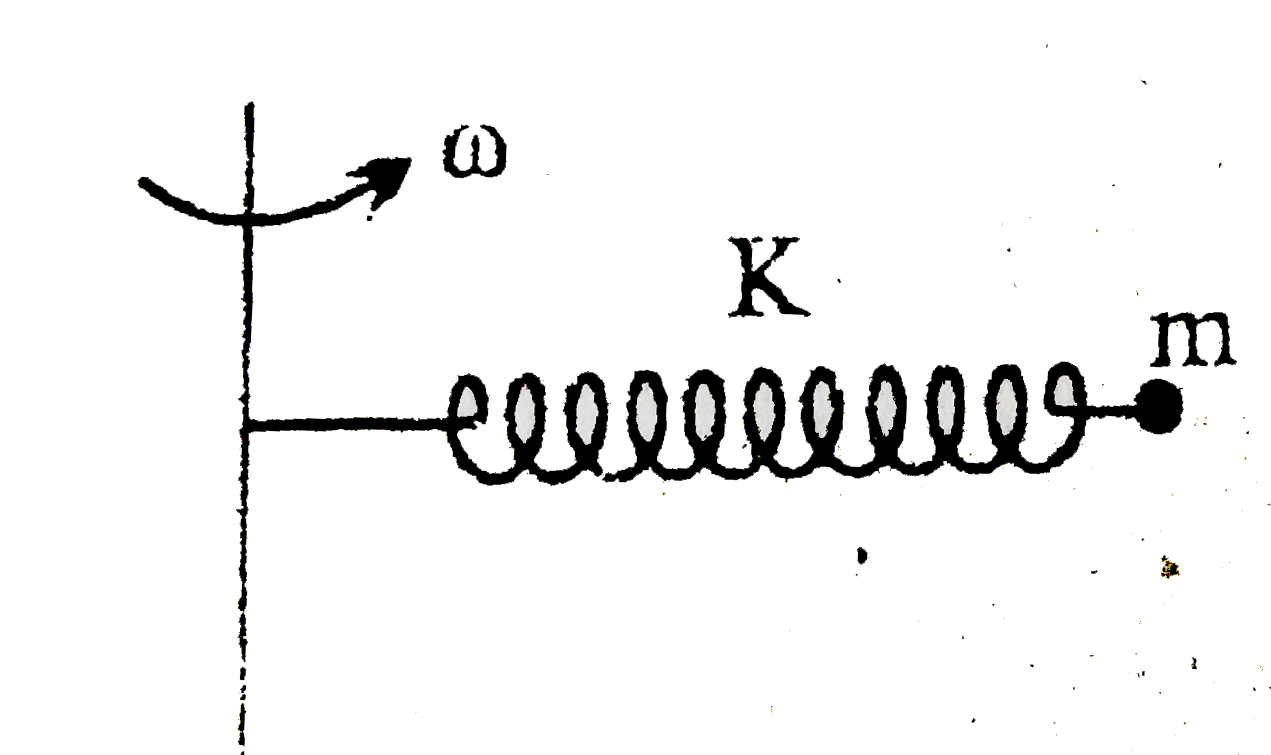 View Solution
View SolutionA block of mass 0.01 kg is attached to a spring of force constant 10−1Nm−1 . If the energy of oscillation is 10−5 J, find the angular frequency and amplitude of oscillation.
View SolutionA constant force(F) is applied on a stationary particle of mass 'm'. the velocity attained by the particle in a certain interval of time will be proportional to
View SolutionA force F is exerted on a body of mass M, which is connected to a spring (spring constant k). The body has a constant acceleration a. Calculate the work done by the external force in moving the body by a distance D.
View Solution

