The Fig. shows a string of equally placed beads of mass m, separated by distance d. The beads are free to slide without friction on a thin wire. A constant force F act on the first bead initially at rest till it makes collision with the second bead. The second bead then collides with the third and so on. Supposed that all collisions are elastic,
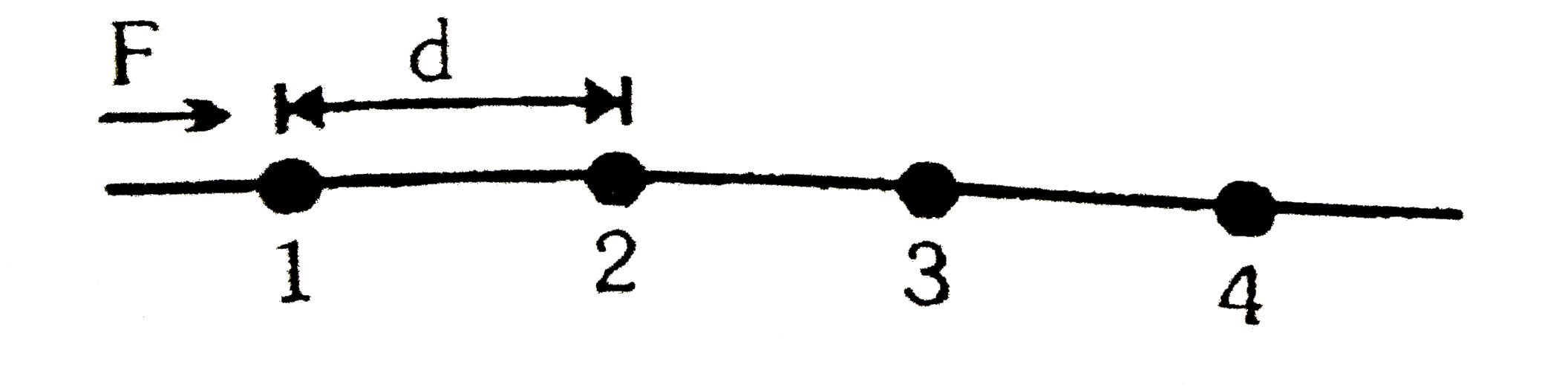
a) Speed of first bead immediately before and immediately after its collision with the second bead is √2Fdm and zero respectively.
b) Speed of first bead immediately before and immediately after its collision with the second bead is √2Fdmand12√2Fdm respectively.
c) Speed of second bead immediately after its collision with the third bead is zero.
d) The average speed of the first bead during its motion is 12√2Fdm.
The correct Answer is:A, C, D
Step by step video & image solution for The Fig. shows a string of equally placed beads of mass m, separated by distance d. The beads are free to slide without friction on a thin wire. A constant force F act on the first bead initially at rest till it makes collision with the second bead. The second bead then collides with the third and so on. Supposed that all collisions are elastic, by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- TEST PAPERSBOOK - ALLENCHAPTER - TEST PAPERSEXERCISE - MATHS
14 Videos
- TEST PAPERSBOOK - ALLENCHAPTER - TEST PAPERSEXERCISE - part-2 physic
48 Videos
- TEST PAPER 4BOOK - ALLENCHAPTER - TEST PAPER 4EXERCISE - PHYSICS
44 Videos
- UNIT & DIMENSIONS, BASIC MATHS AND VECTOR BOOK - ALLENCHAPTER - UNIT & DIMENSIONS, BASIC MATHS AND VECTOR EXERCISE - Exercise (J-A)
7 Videos
Similar Questions
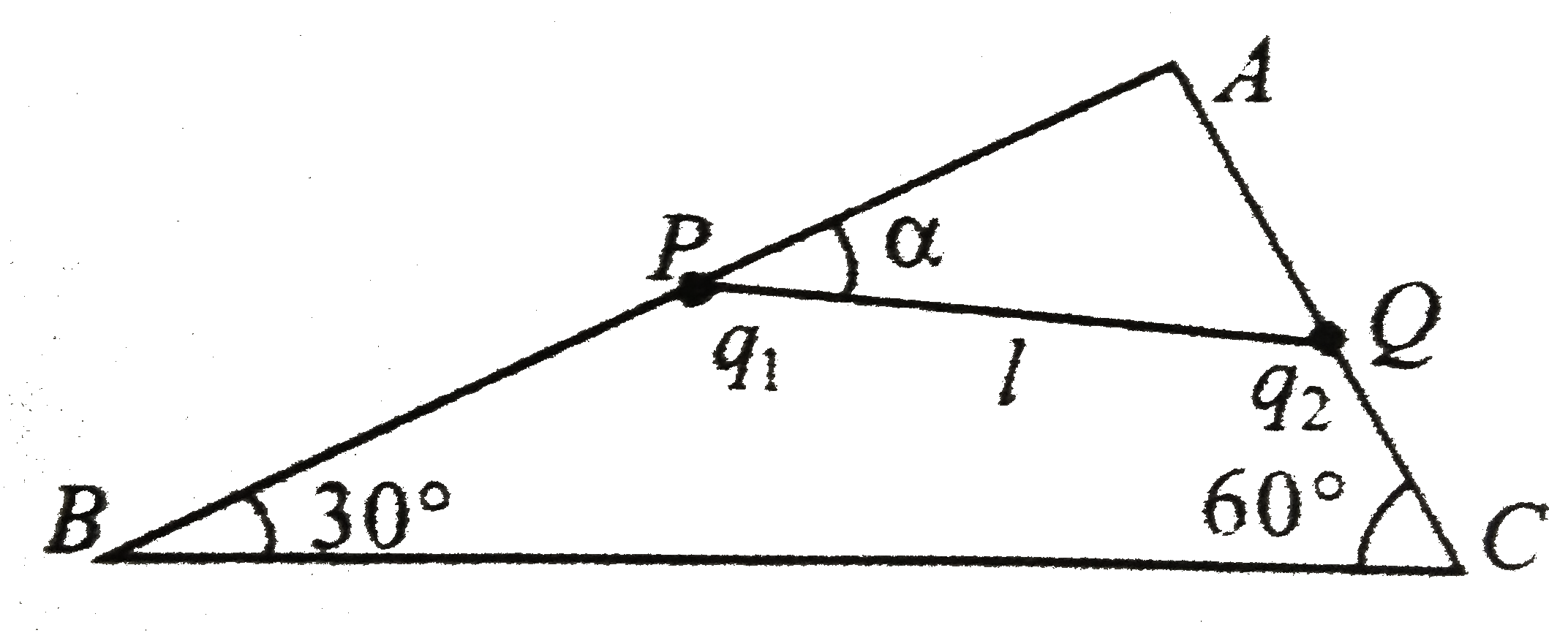
A rigid insulated wire frame in the form of a right-angled triangle ABC is set in a vertical plane as shown in fig. two beads of equal masses m each and carrying charges q1 and q2 are connected by a cord of length l and can slide without friction on the wires.
Cinsidering the case when the beads are stationary, determine
(i) the angel α
(ii) the tension in the cord, and
(iii) The normal recation on teh beads.
If the cord is now cut, what are the value of the charges for which the beads continue to remain stationary?
View SolutionA piece of wire is bent in the shape of a parabola y=kx2 (y-axis vertical) with a bead of mass m on it. The bead can slide on the wire without friction. It stays at the lowest point of the parabola when the wire is at rest. The wire is now accelerated parallel to the x-axis with a constant acceleration a. The distance of the new equilibrium position of the bead, where the bead can stay at rest with respect to the wire, from the y-axis is:
View Solution
Knowledge Check
A piece of wire is bent in the shape of a parabola y=kx2 (y-axis vertical) with a bead of mass m on it. The bead can slide on the wire without friction. It stays at the lowest point of the parabola when the wire is at rest. The wire is now accelerated parallel to the x-axis with a constant acceleration a. The distance of the new equilibrium position of the bead, where the bead can stay at rest with respect to the wire, from the y-axis is:
Aa/gkBa/2gkC2a/gkDa/4gk
A piece of wire is bent in the shape of a parabola y=kx2 (y-axis vertical) with a bead of mass m on it. The bead can slide on the wire without friction. It stays at the lowest point of the parabola when the wire is at rest. The wire is now accelerated parallel to the x-axis with a constant acceleration a. The distance of the new equilibrium position of the bead, where the bead can stay at rest with respect to the wire, from the y-axis is:
View SolutionA piece of wire is bent in the shape of a parabola y=kx2 (y axis vertical) with a bead of mass mon it. The bead can slide on the wire without friction. It stays at the lowest point of the parabola when the wire is at rest. The wire is now accelerated paralle to the x-axis with a constant acceleration a. The distance of the the new equilibrium position of the bead. Find the x-coordinate where the bead can stay at rest with respect to the wire ?
View SolutionA bead of mass m and diameter d is sliding back and forth with velocity v on a wire held between two right walls of length L. Assume that th ecollisions with the wall are perfectly elastic and ther is no friction. The average force that the bouncing bead exerts on the one of the walls is :_
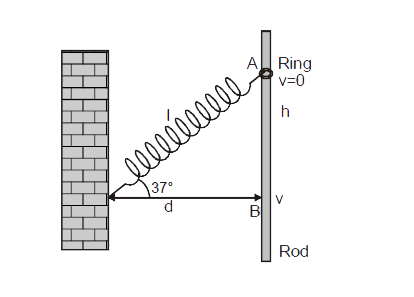
View SolutionOne end of a light spring of natural length d and spring constant k is fixed on a rigid wall and the other is attached to a smooth ring of mass m which can slide without friction on a vertical rod fixed at a distance d from the wall. Initially the spring makes an angle of 37∘ with the horizontal as shown in fig. When the system is released from rest, find the speed of the ring when the spring becomes horizontal.
[ sin 37∘ = 3/5]
View SolutionA horizontal frictionless rod is threaded through a bead of mass m. The length of the cart is L and the radius of the bead, r, is very small in comparison with L(r<<L). Initially at (t=0) the bead is at the right edge of the cart. The can is struck and as a result, it moves with velocity v0 towards right. When the bead collides with the cart's walls, the collisions are always completely elastic.
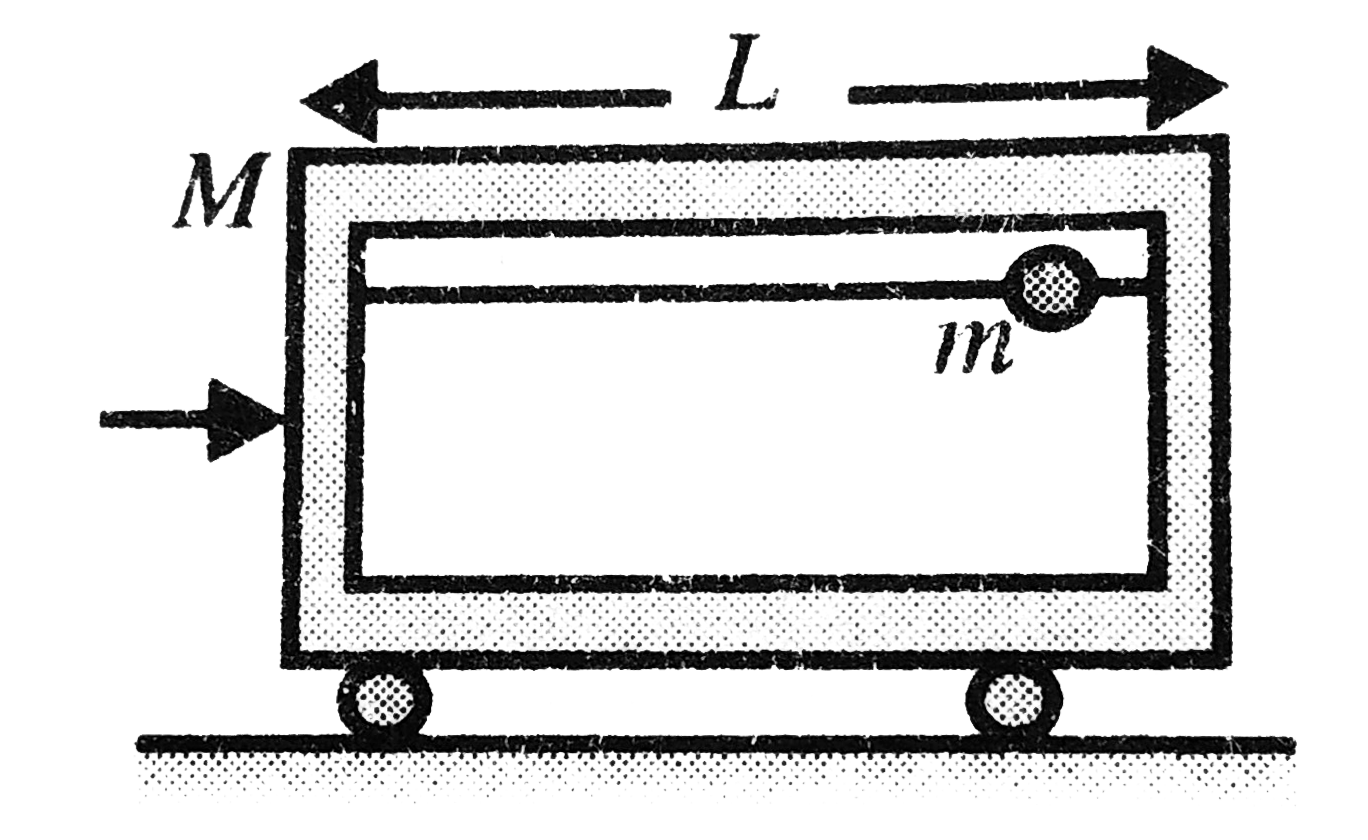
Velocity of bead just after the first collision is
View SolutionA horizontal frictionless rod is threaded through a bead of mass m. The length of the cart is L and the radius of the bead, r, is very small in comparison with L(r<<L). Initially at (t=0) the bead is at the right edge of the cart. The can is struck and as a result, it moves with velocity v0 towards right. When the bead collides with the cart's walls, the collisions are always completely elastic.
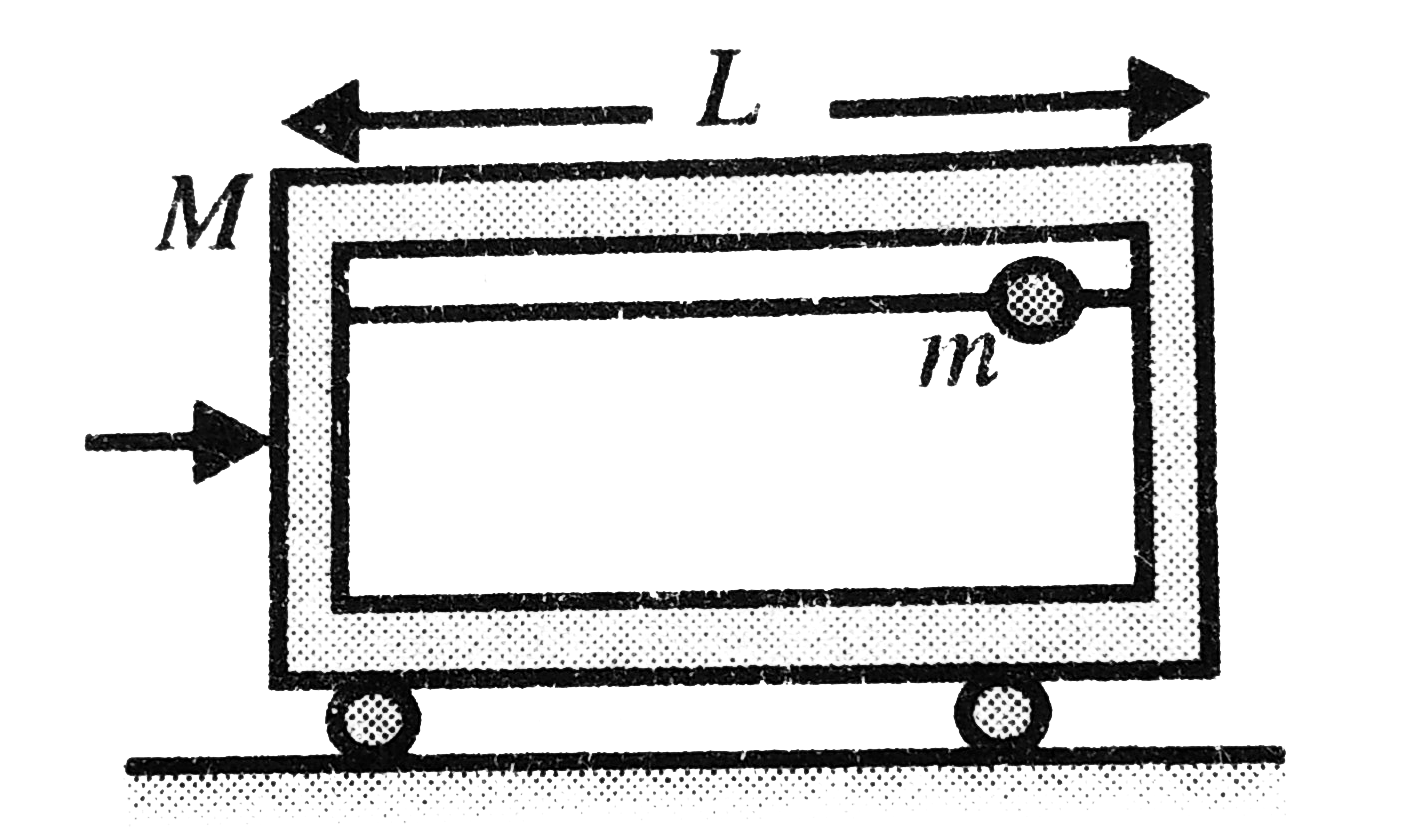
What is the velocity of the cart just after the first collision?
View SolutionA horizontal frictionless rod is threaded through a bead of mass m. The length of the cart is L and the radius of the bead, r, is very small in comparison with L(r<<L). Initially at (t=0) the bead is at the right edge of the cart. The can is struck and as a result, it moves with velocity v0 towards right. When the bead collides with the cart's walls, the collisions are always completely elastic.
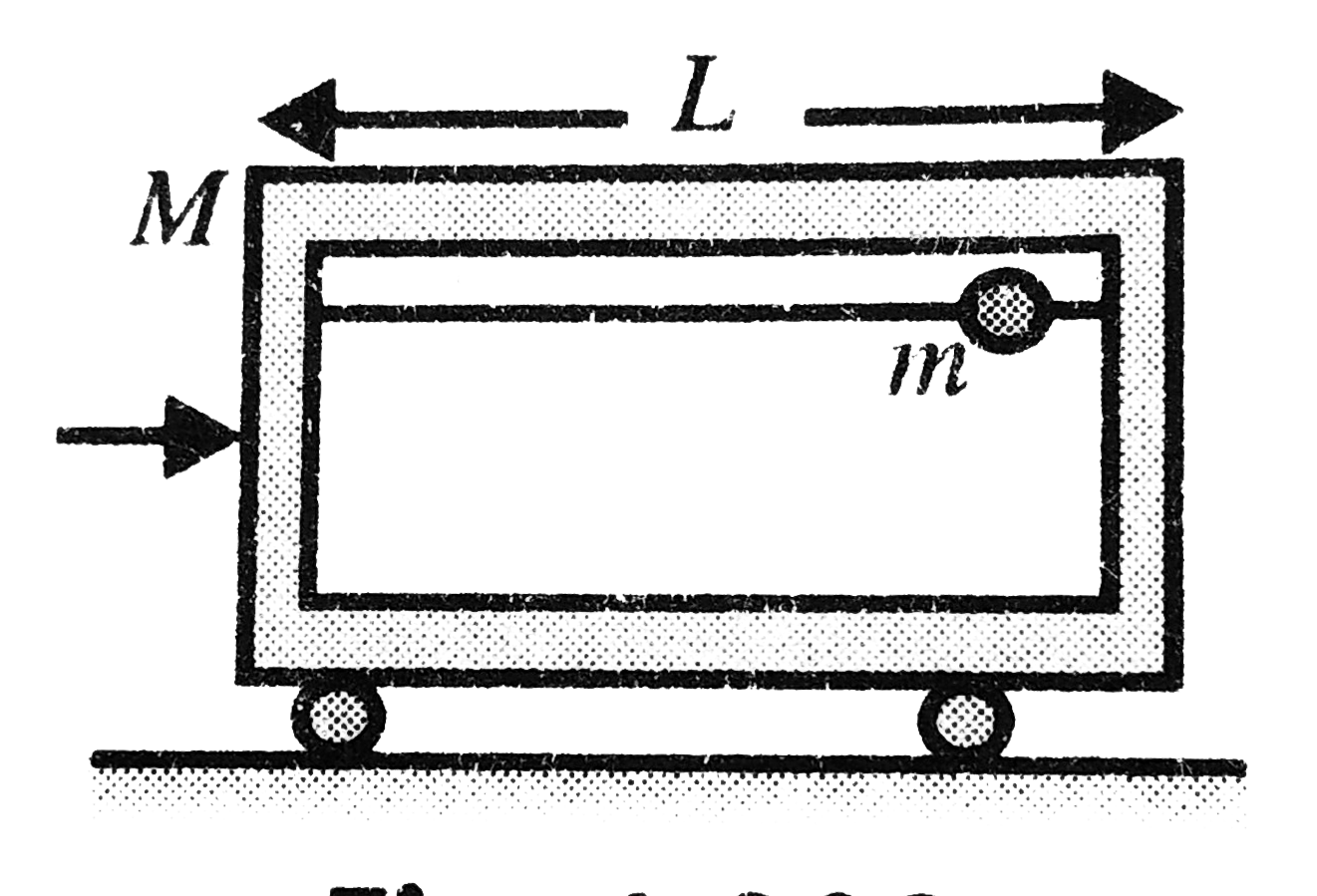
The first collision takes place at time ti and the second collision takes place at time t2. Find t2−t1
View Solution
