A particle leaves the origin with initial velocity →v0=11ˆi+14ˆjm/s. It undergoes a constant acceleration given by →a=−225ˆi+215ˆjm/s2.
When does the particle cross the y-axis ?
2 sec
4 sec
5 sec
7 sec
The correct Answer is:C
To solve the problem of when the particle crosses the y-axis, we need to analyze the motion of the particle in the x and y directions separately. The particle starts at the origin with an initial velocity and experiences a constant acceleration.
1. Identify the Initial Conditions:
- Initial velocity: →v0=11^i+14^jm/s
- Initial position: →r0=0^i+0^jm
- Acceleration: →a=−225^i+215^jm/s2
2. Determine the Displacement Equations:
The displacement in the x-direction can be described by the equation of motion:
x(t)=x0+v0xt+12axt2
Where:
- x0=0
- v0x=11m/s
- ax=−225m/s2
Thus, the equation becomes:
x(t)=11t−2210t2=11t−115t2
3. Set the x-displacement to Zero:
To find when the particle crosses the y-axis, we set x(t)=0:
11t−115t2=0
4. Factor the Equation:
Factoring out t:
t(11−115t)=0
This gives us two solutions:
- t=0 (the initial time)
- 11−115t=0
5. Solve for t:
Solving the second equation:
11=115t
t=11×511=5seconds
6. Conclusion:
The particle crosses the y-axis at t=5 seconds.
Final Answer:
The particle crosses the y-axis at t=5 seconds.
---
- Initial velocity: →v0=11^i+14^jm/s
- Initial position: →r0=0^i+0^jm
- Acceleration: →a=−225^i+215^jm/s2
The displacement in the x-direction can be described by the equation of motion:
x(t)=x0+v0xt+12axt2
Where:
- x0=0
- v0x=11m/s
- ax=−225m/s2
x(t)=11t−2210t2=11t−115t2
To find when the particle crosses the y-axis, we set x(t)=0:
11t−115t2=0
Factoring out t:
t(11−115t)=0
This gives us two solutions:
- t=0 (the initial time)
- 11−115t=0
Solving the second equation:
11=115t
t=11×511=5seconds
The particle crosses the y-axis at t=5 seconds.
The particle crosses the y-axis at t=5 seconds.
Topper's Solved these Questions
- KINEMATICS-2DBOOK - ALLENCHAPTER - KINEMATICS-2DEXERCISE - Exercise (O-2)
46 Videos
- KINEMATICS-2DBOOK - ALLENCHAPTER - KINEMATICS-2DEXERCISE - Exercise (S-2)
15 Videos
- GRAVITATIONBOOK - ALLENCHAPTER - GRAVITATIONEXERCISE - EXERCISE 4
9 Videos
- MOTION IN A PALNEBOOK - ALLENCHAPTER - MOTION IN A PALNEEXERCISE - SOLVED EXAMPLE
28 Videos
Similar Questions
A particle leaves the origin with an lintial veloity →u=(3ˆi) and a constant acceleration →a=(−1.0ˆi−05ˆj)ms−1. Its velocity →v and position vector →r when it reaches its maximum x-coordinate aer .
View SolutionStarting from origin at t=0, with initial velocity 5ˆjm/s, a particle moves in the x−y plane with a constant acceleration of (10ˆi−5ˆj)m/s2. Find the coordinates of the particle at the moment its y-coordinate is maximum.
View SolutionA particle is moving with a constant acceleration →a=ˆi−2ˆjm/s2 and instantaneous velocity →v=ˆi+2ˆj+2ˆkm/s then rate of change of speed of particle 1 second after this instant will be :
View SolutionA particle of mass 2kg is moving with velocity →v0=(2ˆi−3ˆj)m/s in free space. Find its velocity 3s after a constant force →F=(3ˆi+4ˆj)N starts acting on it.
View SolutionA particle is moving in x-y plane. At an instant, it has velocity (4ˆi+4ˆj)m/s and acceleration (3ˆi+5ˆj)m/s2 At that instant, the radius of curvature of its path will be :
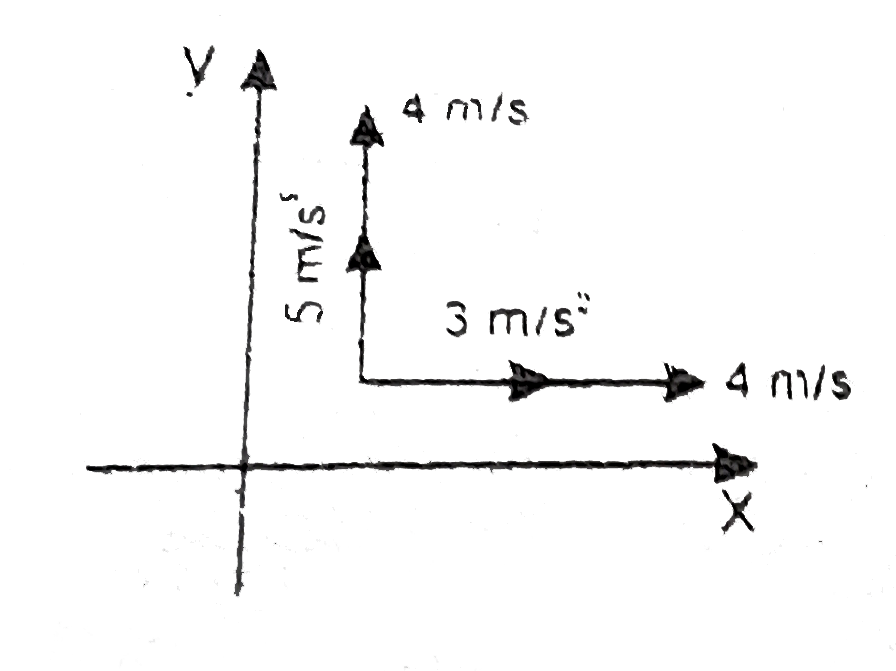
View SolutionA particle has initial velocity of (3ˆi+4ˆj)m/s and a acceleration of (4ˆi−3ˆj)m/s2. Its speed after one second will be equal to :-
View SolutionA projectile is projected in air with initial velocity →v=(3ˆi+4ˆj) m/s from the origin. The equation of trajectory of the projectile is given as (g=−10ˆjms2) (neglect air resistance )
View SolutionTwo particles of equal mass have velocities →v1=2ˆi=m/s−1 and →v2=2ˆjm/s−1. First particle has an acceleration →a1=(3ˆi+3ˆj)ms−2 while the acceleration of the other particle is zero. The centre of mass of the two particles moves in a path of.
View SolutionA particle has an initial velocity of 3ˆi+4ˆj and an acceleration of 0.4ˆi+0.3ˆj. Its speed after 10s is :
View SolutionA particle has an initial velocity of 3ˆi+4ˆj and an acceleration of 0.4ˆi+0.3ˆj. Its speed after 10s is :
View Solution
