An onject intially att rest moves along x-axis subjected to an acceleration which veries with time according to relation a=2t+5. Its velocity after 2 seconds will be :-
18ms−1
9ms−1
12ms−1
14ms−1
The correct Answer is:D
To find the velocity of the object after 2 seconds, we can follow these steps:
Step 1: Understand the given information
The acceleration a of the object is given by the equation:
a=2t+5
The object starts from rest, which means its initial velocity v0=0.
Step 2: Relate acceleration to velocity
Acceleration is the rate of change of velocity with respect to time. Therefore, we can express this relationship as:
a=dvdt
We can substitute the expression for acceleration into this equation:
dvdt=2t+5
Step 3: Integrate the acceleration to find velocity
To find the velocity v, we need to integrate the acceleration with respect to time:
v=∫(2t+5)dt
This can be separated into two integrals:
v=∫2tdt+∫5dt
Step 4: Perform the integration
Now we can perform the integration:
1. The integral of 2t is t2.
2. The integral of 5 is 5t.
Thus, we have:
v=t2+5t+C
where C is the constant of integration.
Step 5: Apply the initial condition
Since the object starts from rest, we know that when t=0, v=0:
0=02+5(0)+C⟹C=0
So the expression for velocity simplifies to:
v=t2+5t
Step 6: Calculate the velocity at t=2 seconds
Now we can substitute t=2 seconds into the velocity equation:
v=(2)2+5(2)
Calculating this gives:
v=4+10=14m/s
Final Answer
The velocity of the object after 2 seconds is:
14m/s
The acceleration a of the object is given by the equation:
a=2t+5
The object starts from rest, which means its initial velocity v0=0.
Acceleration is the rate of change of velocity with respect to time. Therefore, we can express this relationship as:
a=dvdt
We can substitute the expression for acceleration into this equation:
dvdt=2t+5
To find the velocity v, we need to integrate the acceleration with respect to time:
v=∫(2t+5)dt
This can be separated into two integrals:
v=∫2tdt+∫5dt
Now we can perform the integration:
1. The integral of 2t is t2.
2. The integral of 5 is 5t.
v=t2+5t+C
where C is the constant of integration.
Since the object starts from rest, we know that when t=0, v=0:
0=02+5(0)+C⟹C=0
So the expression for velocity simplifies to:
v=t2+5t
Now we can substitute t=2 seconds into the velocity equation:
v=(2)2+5(2)
Calculating this gives:
v=4+10=14m/s
The velocity of the object after 2 seconds is:
14m/s
Topper's Solved these Questions
- RACEBOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (Graphs))
29 Videos
- RACEBOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (Co-ordinate & Algebra)
37 Videos
- RACEBOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (Differentiation)
38 Videos
- NEWTONS LAWS OF MOTIONBOOK - ALLENCHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - EXERCISE-III
28 Videos
- SIMPLE HARMONIC MOTIONBOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Example
1 Videos
Similar Questions
The acceleration of a particle which starts from rest varies with time according to relation a=2t+3. The velocity of the particle at time t would be
View SolutionA point initially at rest moves along x-axis. Its acceleration varies with time as a=(6t+5)m/s2. If it starts from origin, the distance covered in 2 s is:
View Solution
Knowledge Check
The figure shows a particle moving along x - axis subjected to three particles of acceleration (a). Rank the periods according to the increase they produce in the particle velocity, greatest first.
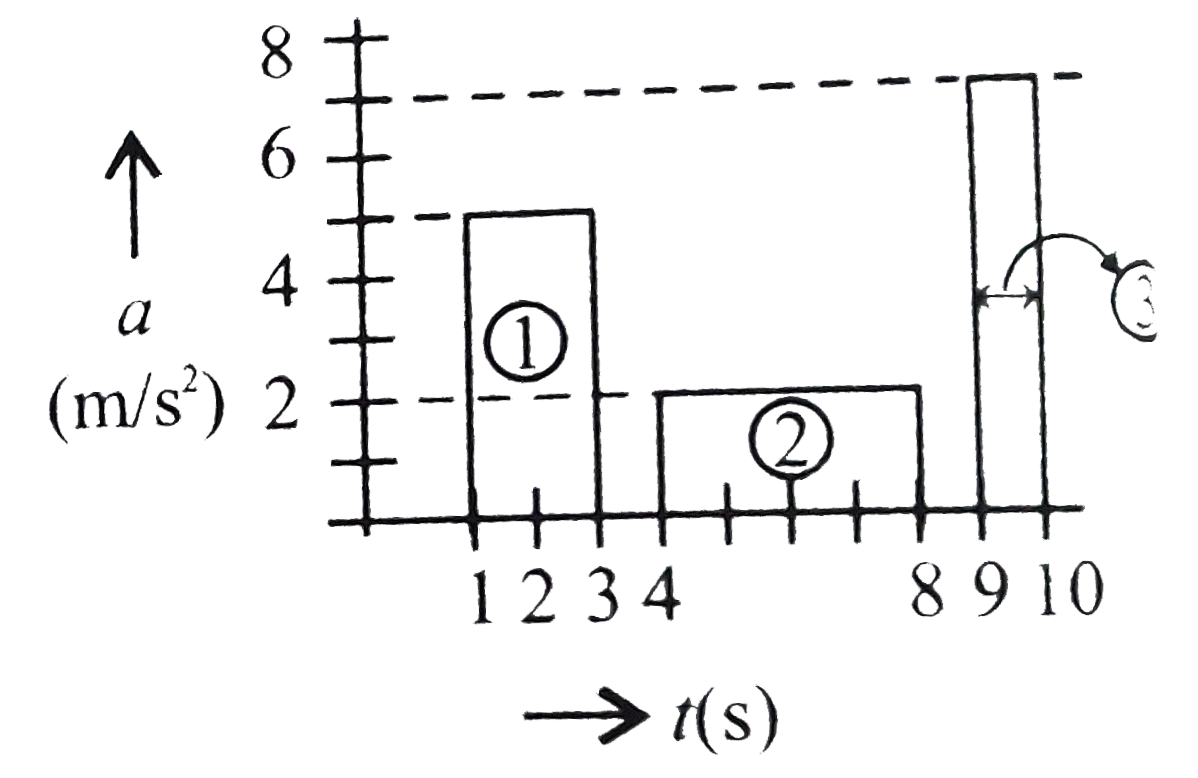 A
A B
B C
C D
D
The acceleration of a'particle starting from rest, varies with time according to the relation a=kt+c. The velocity of the particle after time t will be :
View SolutionAn object moves along x-axis such that its position varies with time according to the relation x=50t−5t2
Here, x is in meters and time is in seconds. Find the displacement and distance travelled for the time interval t = 0 to t = 6 s.
View SolutionThe position x of a particle varies with time t according to the relation x=t3+3t2+2t. Find the velocity and acceleration as functions of time.
View SolutionA particle moves along X-axis in such a way that its coordinate X varies with time t according to the equation x=(2−5t+6t2)m. The initial velocity of the particle is
View SolutionA body moves along x-axis such that its displacement varies with time as given, x=7+3t+5t2. The average velocity during 3rd second is
View SolutionA particle moves along x - axis in such a way that its x - co - ordinate varies with time according to the equation x=4−2t+t2. The speed of the particle will vary with time as
View SolutionIf v is the velocity of a body moving along x-axis, then acceleration of body is
View Solution
